 |
Основные свойства характеристической функции
|
|
|
|
Рассмотрим свойства функции 
для непрерывной случайной величины. Для дискретной величины эти свойства доказываются аналогично.
1). В общем случае характеристическая функция (46.2) является комплексной. Ее вещественная часть
(47.1)
- является 
- преобразованием от плотности вероятности, и мнимая часть
(47.2)
- является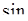 
- преобразованием от 
. Если 
- четная функция, то 
, тогда характеристическая функция 
и является вещественной и четной функцией.
2). 
. Это свойство следует из (46.2) и условия нормировки для плотности:
. (47.3)
3). 
- функция 
имеет глобальный максимум в точке 
. Доказательство следует из (46.2):
.
4). 
5). Характеристическая функция непрерывна. Для доказательства рассмотрим приращение 
аргумента функции 
, такое, что 
, где 
- положительное число. Тогда имеет место следующая цепочка преобразований: 
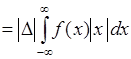. (47.4)
Пусть 
и число
, (47.5)
тогда из (47.4) следует
. (47.6)
Таким образом, выполняется определение непрерывности функции 
: для любого 
можно выбрать положительное 
, что из условия 
следует 
.
Примеры вычисления характеристической функции
48.1. Пусть 
- случайная величина с характеристической функцией 
. Найти характеристическую функцию 
случайной величины
, (48.1)
где 
- числа. По определению
. (48.2)
48.2. Найти характеристическую функцию 
гауссовой случайной величины 
. По формуле (46.2)
. (48.3)
Выполним замену переменной интегрирования 
на переменную 
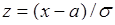, тогда 
и
|
|
|
. (48.4)
Показатель в подынтегральном выражении преобразуем следующим образом:
.
Подстановка этого результата в (48.4) приводит к выражению
. (48.5)
Отсюда следует, что характеристическая функция гауссовой случайной величины при 
является вещественной и четной функцией.
Моменты, кумулянты и характеристическая функция
49.1. Вычислим производную порядка 
характеристической функции (46.1) при 
:
, (49.1)
где 
- начальный момент 
порядка случайной величины 
. Пусть существуют все моменты 
, 
, тогда существуют производные (49.1) характеристической функции при . Поэтому функцию можно разложить в ряд Тейлора около точки :
. (49.2)
Отметим, что здесь первое слагаемое 
. Выражение (49.2) называют иногда разложением характеристической функции по моментам, имея ввиду тот факт, что коэффициенты при 
определяются начальными моментами 
.
Для непрерывной случайной величины с плотностью вероятности соотношение (49.1) можно представить в виде:
. (49.3)
Таким образом, существование производной порядка характеристической функции при (или начального момента 
) определяется поведением плотности вероятности при 
, от которого зависит существование интеграла (49.3).
49.2. Функция
(49.4)
называется кумулянтной функцией случайной величины 
. Кумулянтная функция является полной вероятностной характеристикой случайной величины, также, как и 
. Смысл введения кумулянтной фукнции заключается в том, что эта функция зачастую оказывается наиболее простой среди полных вероятностных характеристик, т.е. среди 
. Например, для гауссовой случайной величины из (48.5) следует
. (49.5)
Кумулянтную функцию можно представить рядом, аналогично соотношению (49.2) для характеристической функции:
|
|
|
, (49.6)
где число
(49.7)
называется кумулянтом порядка случайной величины . Из (49.7) следует 
, поэтому суммирование в (49.6) можно начинать с 
, а поскольку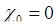 
для любой случайной величины, то 
не является характеристикой случайной величины.
Вычислим кумулянты для гауссовой случайной величины. Из (49.7), (49.5)
, (49.8)
. (49.9)
Для 
производная 
, следовательно, гауссова случайная величина имеет только два кумулянта 
и 
отличных от нуля, остальные кумулянты - нулевые. Поэтому ряд (49.6) для гауссовой величины состоит из двух слагаемых.
|
|
|
