 |
Моменты случайной величины
|
|
|
|
41.1. Математическое ожидание и дисперсия являются примерами моментов случайной величины, которые определяются следующим образом.
Начальным моментом порядка 
непрерывной случайной величины с плотностью распределения вероятности 
называется число
. (41.1)
Порядок момента - это неотрицательное целое число, т.е. 
.
Начальным моментом порядка 
дискретной случайной величины 
, принимающей значения 
с вероятностями 
, 
, называется число
. (41.2)
Определение (41.1) можно рассматривать как универсальное определение для непрерывных и для дискретных случайных величин. В последнем случае плотность вероятности выражается через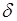 
- функцию согласно формуле (34.4). Однако на практике для вычисления момента дискретной величины удобнее использовать соотношение (41.2).
Центральным моментом порядка случайной величины 
называется число
. (41.3)
Для непрерывной случайной величины с плотностью вероятности 
центральный момент порядка 
имеет вид:
. (41.4)
41.2. Из всего множества начальных и центральных моментов обычно используются моменты невысоких порядков, до 
включительно, как более простые характеристики случайной величины. Применение моментов высоких порядков, 
, ограничено. Во-первых, при больших 
моменты могут не существовать, поскольку могут расходиться интегралы (41.1), (41.4). И во-вторых, интерпретация моментов высших порядков затруднена.
Рассмотрим начальные моменты, начиная с 
. При этом из (41.1) следует
. (41.5)
Итак, начальный момент нулевого порядка 
для любой случайной величины, следовательно, этот момент не отражает каких-либо свойств случайной величины, т.е. не является ее характеристикой. При 
из (41.1) следует, что момент первого порядка - это математическое ожидание случайной величины. Разные случайные величины могут иметь разные математические ожидания, и поэтому число 
является характеристикой случайной величины: число 
указывает положение центра ее плотности вероятности.
|
|
|
Момент второго порядка
(41.6)
- это среднее квадрата 
случайной величины, и т.д.
Рассмотрим аналогично центральные моменты (41.4). При 
получаем 
- одинаковый результат для любой случайной величины. Поэтому данный момент не является характеристикой случайной величины, поскольку не отражает каких-либо ее свойств. При 
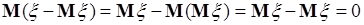. Этот результат также одинаков для любой случайной величины, поэтому центральный момент первого порядка не является характеристикой случайной величины. При 
из (41.4) получаем дисперсию
(41.7)
- важнейшую числовую характеристику случайной величины и т.д.
Моменты третьего и четвертого порядков будут рассмотрены в дальнейшем.
Неравенство Чебышева
42.1. Пусть случайная величина имеет конечный момент второго порядка 
, тогда
, (42.1)
где 
- любое действительное число и 
. Соотношение (42.1) называют неравенством Чебышева.
Сначала рассмотрим доказательство неравенства, следующего из (42.1) при 
:
. (42.2)
Доказательство неравенства Чебышева удобнее рассматривать отдельно для непрерывной и для дискретной случайных величин. При этом доказательства являются относительно простыми, а ход доказательств вполне очевиден. В то время как универсальное доказательство, справедливое и для непрерывной и для дискретной случайных величин оказывается значительно более сложным. Рассмотрим непрерывную случайную величину с плотностью вероятности . Тогда в соотношении 
первое слагаемое можно представить в виде
|
|
|
,
поэтому
.
Здесь использовано неравенство 
- справедливое на области интегрирования. Полученное выражение совпадает с неравенством (42.2). Аналогично выполняется доказательство для дискретной случайной величины.
Теперь случайную величину 
в (42.2) можно заменить на случайную величину 
, где - любое действительное число, тогда из (42.2) следует неравенство Чебышева (42.1). Это неравенство определяет границу сверху для вероятности 
или, как говорят, больших уклонений 
случайной величины 
от числа . Большие уклонения понимаются в смысле их превышения над заданным числом 
.
42.2. Пусть 
, тогда неравенство Чебышева (42.1) имеет вид
. (42.3)
Теперь минимальное уклонение 
можно измерять в единицах среднеквадратического уклонения 
случайной величины , т.е. положить
, (42.4)
где - коэффициент пропорциональности. Подставим (42.4) в (42.3), тогда
. (42.5)
Если правая часть 
, то (42.5) не представляет какого-либо ограничения на случайную величину, поскольку вероятность 
не может выходить за пределы интервала 
. Поэтому коэффициент в (42.5) имеет смысл рассматривать только большим: 
. Отсюда очевидна интерпретация неравенства Чебышева как неравенства, определяющего границу сверху вероятности больших уклонений.
Пусть 
- непрерывная случайная величина с плотностью вероятности 
, тогда неравенству Чебышева (42.1) можно дать простую геометрическую интерпретацию, представленную на рис. 42.1.
Рис. 42.1. Иллюстрация к неравенству Чебышева.
Здесь указаны числа , 
и 
, заштрихованная площадь - это вероятность
.
Коэффициент асимметрии
Среднее и дисперсия случайной величины - это числа, которые определяют такие свойства ее плотности вероятности как положение центра и эффективную ширину. Очевидно, эти два числа не отражают всех особенностей плотности, в частности, степень симметрии или асимметрии плотности относительно математического ожидания - это новая характеристика, которую можно определить как некоторое число.
|
|
|
Для любой симметричной плотности 
центральные моменты нечетного порядка равны нулю (доказательство приводится ниже). Поэтому простейший среди них - центральный момент третьего порядка может характеризовать асимметрию плотности распределения:
, (43.1)
где 
- математическое ожидание, 
- центральный момент - го порядка.
Асимметрию принято характеризовать коэффициентом асимметрии
, (43.2)
где 
- дисперсия случайной величины .
Рассмотрим доказательство утверждения о том, что для симметричной плотности 
центральные моменты нечетных порядков равны нулю.
1). Пусть - симметричная функция относительно некоторой точки 
, тогда
, (43.3)
поскольку 
- антисимметричная функция относительно 
. Отсюда следует:
. (43.4)
Таким образом, если - симметричная функция относительно точки , то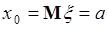 
- точка симметрии плотности вероятности – это математическое ожидание случайной величины.
2). Пусть 
- нечетное целое и - симметричная функция, тогда 
, поскольку - симметрична относительно математического ожидания , и 
- антисимметрична относительно .
Выражение (43.2) для можно представить через начальные моменты 
, 
. Из определения следует:
.
Аналогично центральный момент третьего порядка
.
Пусть случайная величина имеет плотность вероятности:
, (43.6)
(распределение Рэлея), тогда вычисление 
и подстановка в (43.2) приводит к результату 
.
Плотность вероятности с 
имеет более тяжелый «хвост» в области больших положительных аргументов, и наоборот, при 
более тяжелым является «хвост» плотности в области отрицательных аргументов.
Коэффициент эксцесса
Характеристикой степени сглаженности вершины плотности вероятности является число
, (43.1)
|
|
|
называемое коэффициентом эксцесса.
Определим 
для нормального распределения. Поскольку 
, то осталось вычислить
.
Пусть 
, тогда
.
Вычислим интеграл способом «по частям»:
.
Таким образом, 
. Подставим полученные результаты в (43.6), тогда 
.
Если 
, то плотность вероятности имеет более высокую и более острую вершину, чем кривая плотности нормального распределения с той же дисперсией. Если 
, то вершина плотности распределения более плоская, чем у нормального распределения.
|
|
|
