 |
Виды систем массового обслуживания
|
|
|
|
В зависимости от того, как поступают с заявкой в случае, если все каналы оказались занятыми, различают:
СМО с отказом в обслуживании заявки и СМО с ожиданием.
Для СМО с отказом характерно, что заявка, заставшая все каналы занятыми, немедленно покидает систему.
В СМО с ожиданием заявка, заставшая все каналы занятыми, не покидает систему, а ставится в очередь и при освобождении одного из каналов обслуживается. В СМО с ожиданием на процесс ожидания заявок в очереди могут накладываться или не накладываться какие-либо ограничения. В последнем случае говорят, что имеют дело с "чистой" СМО с ожиданием. Если же на процесс ожидания накладываются ограничения, то СМО называют "системой смешанного типа". В таких системах из-за наложенных ограничений возможны случаи, когда заявка получит отказ в обслуживании, т.е. СМО смешанного типа проявляет также признаки СМО с отказом.
В системах смешанного типа могут накладываться следующие ограничения:
а) на количество заявок, стоящих в очереди;
б) на время пребывания заявки в очереди;
в) на общее время нахождения заявки в СМО.
В технологии РЭУ чаще всего встречаются СМО смешанного типа.
Математическое описание СМО с отказом
Рассмотрим систему массового обслуживания с отказом, имеющую п каналов. Предположим, что поток заявок, поступающих в СМО, простейший и имеет плотность l. Кроме того, будем считать, что время обслуживания заявок распределено по экспоненциальному закону с параметром

где М(Тоб) — математическое ожидание времени обслуживания заявки.
Следовательно, плотность распределения времени обслуживания

Для рассматриваемой системы возможны следующие состояния:
|
|
|
x0 — свободны все каналы;
x1 — занят один канал;
¼
xk -- занято k каналов;
¼
xn-- заняты все п каналов.
Данные состояния системы обслуживания могут быть описаны дифференциальными уравнениями Эрланга[18]. их решение позволяет получить формулы для расчета вероятностей, которые для установившегося режима постоянны. Такой режим наступает при времени t® ¥.

| где | pk -- вероятность состояния хk; |
| a — приведенная плотность заявок или коэффициент загрузки канала. |
Коэффициент определяют как

где М(Тоб) — математическое ожидание времени обслуживания одной заявки.
Формулы Эрланга получены для случая экспоненциального распределения времени обслуживания, но справедливы и при любом другом законе, лишь бы поток заявок был простейшим.
Вероятность необслуживания заявки определяется как

Относительная пропускная способность q
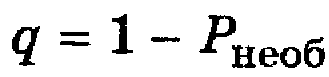
Среднюю долю времени, которое система обслуживания будет простаивать, можно определить вероятностью состояния x0, т.е.
Рпростоя = р(х0) = р0
Пример. Пусть на участок ремонта технологического оборудования поступают приборы со средней плотностью l = 2 ед/ч. Среднее время обслуживания одной единицы оборудования равно 24 мин (0,4 ч.). Заявка, заставшая все каналы занятыми получает отказ в обслуживании.
Требуется определить характеристики СМО в предположении наличия одного рабочего места. Кроме того, требуется установить, как меняются характеристики СМО при введении второго рабочего места.
Решение. По условию задачи имеем СМО с отказом. Будем предполагать, что поток заявок, поступающих в СМО, простейший со средней плотностью l.
1. Подсчитаем коэффициент загрузки канала или приведенную плотность заявок
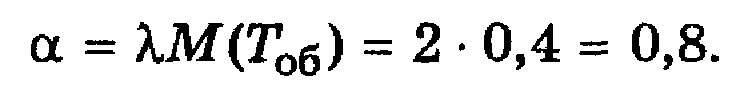
2. Найдем характеристики СМО при числе каналов n = 1. Вероятность необслуживания заявок:

Относительная пропускная способность q определится, как
q=1- Рнеоб = 1 – 0,44 = 0,56.
|
|
|
Следовательно, примерно 56% заявок, поступивших в СМО, будут обслужены.
Вероятность простоя канала р0

3. Определим, как меняются характеристики системы с введением второго канала. Для этого подсчитаем характеристики СМО при значении п = 2. Получим:

Относительная пропускная способность q = 0,85 или 85%,а доля времени простоя системы уменьшилась до 47%.
Математическое описание "чистой" СМО с ожиданием
Пусть для этой системы имеют место те же условия, что и для рассмотренной СМО с отказом. Но здесь на процесс ожидания заявок в очереди не накладывается никаких ограничений. Поэтому данная система имеет бесконечное, но счетное число состояний, а именно:
x0 – свободны все каналы;
x1 – занят один канал;
¼
xk – занято k каналов;
¼
xn – заняты все п каналов;
xn+1 -- заняты все п каналов и одна заявка в очереди;
xn+2 -- заняты все п каналов и две заявки в очереди;
¼
xn+s -- заняты все п каналов и s заявок в очереди;
¼.
Решение дифференциальных уравнений Эрланга, описывающих указанные состояния системы, дает следующие формулы для расчета вероятностей состояний для установившегося режима:

Для рассматриваемой СМО установившийся режим наступает в случае, когда коэффициент загрузки канала a < п. Если указанное условие не выполняется, то число заявок, стоящих в очереди, будет неограниченно возрастать, и установившийся режим не наступит.
Для "чистой" СМО с ожиданием важной характеристикой является среднее время ожидания заявки в очереди М(Тож).
Дляустановившегося режима, т.е. когда a< п

где m – плотность потока обслуживания заявок.
Предполагая, что время обслуживания заявок распределено по экспоненциальному закону, плотность их обслуживания

Среднее число заявок, находящихся в очереди, определяется как

Математическое описание СМО смешанного типа с ограничением длины очереди
Пусть СМО имеет п каналов, а число заявок, стоящих в очереди ограничено значением т.
Как и ранее, поток поступающих заявок будем считать простейшим с плотностью l. Пусть также известно среднее время обслуживания одной заявки М(Тоб). Данная система может иметь следующие состояния:
x0 — свободны все каналы;
x1 — занят один канал;
¼
xk -- занято k каналов;
|
|
|
¼
xn-- заняты все п каналов;
xn+1 -- заняты все п каналов и одна заявка в очереди;
xn+2 -- заняты все п каналов и две заявки в очереди;
¼
xn+s -- заняты все п каналов и s заявок в очереди;
¼
xn+m -- заняты все п каналов и m заявок в очереди
Решение дифференциальных уравнений Эрланга, описывающих указанные состояния системы, дает следующие расчетныерасчётные формулы для вероятностей состояний этой системы в случае установившегося режима, который наступает при t®¥.

Очевидно, что вероятность необслуживания заявки определяется вероятностью состояния хn+т т.е.
рнеоб = р (хn+т) = рn+т
Доля времени, которое СМО будет простаивать, как и ранее, определится вероятностью р0.
Пример. На участок ремонта поступают устройства со средней плотностью 2 блока в час. Среднее время ремонта одного блока равно 27 мин (0,45 ч.).
Требуется определить характеристики системы в случае одного и двух рабочих мест при условии, что в помещении дополнительно для ожидания в очереди можно поставить три блока (m=3).
Решение. Согласно условию участок ремонта может рассматриваться как СМО смешанного типа с ограничением числа заявок, стоящих в очереди. Будем считать, что поток заявок, поступающих в СМО, является простейшим, со средней плотностью l.
1. По условию примера имеем
т = 3;
l = 2 бл/ч;
М(Тоб) = 27 мин = 0,45 ч.
Следовательно
a = lМ(Тоб) = 2×0,45= 0,9
2. Определим характеристики СМО при количестве каналов п = 1 для случая установившегося режима. Вероятность необслуживания
рнеоб = рn+т = р1+3=0,16
3. Относительная пропускная способность СМО
q=1- Рнеоб = 1 – 0,16 = 0,84.
т.е. обслужено будет примерно 84% заявок.
4. Абсолютная пропускная способность
Q = ql = 1,68 бл/ч.
5. Средняя доля времени, которое СМО будет простаивать
Ро = P(хo) = 0,24. т.е. примерно четверть.
6. Если количество каналов п = 2, то характеристики СМО для случая установившегося режима будут иметь следующие значения:
рнеоб =0,009
q = 0,991;
Q»1,98 бл/ч;
p0 = 0,34.
Из приведенных характеристик видно, что примерно 99% заявок будет обслужено, но, в то же время при продолжительности рабочей смены 7 часов СМО будет простаивать примерно 2,5 часа =7×0,34.
|
|
|
|
|
|


