Самоорганизация различных стстем и

  СЕНЕРГЕТИКА.

Переход от хаоса к порядку, происходящий при изменении значений параметров от до критических к сверхкритическим, изменяет симметрию системы. По этому такой переход аналогичен термодинамическим фазовым переходам. Переходы в неравновесных процессах называются кинетическими фазовыми переходами. В близи неравновесных фазовых переходов не существует непротиворечивого макроскопического описания. Флуктуации столь же важны, как и среднее значении. Например, макроскопические флуктуации могут приводить к новым типам не устойчивостей.

Итак, в дали от равновесия между химической, кинетической и пространственно-временной структурой реагирующих систем существует неожиданная связь. Правда, взаимодействие, определяющие взаимодействие констант скоростей и коэффициентов переноса, обусловлены короткодействующими силами (силами валентности, водородными связями и силами Ван-Дер-Вальса). Однако решения соответствующих уравнений зависят, кроме того, от глобальных характеристик. Для возникновения диссипативных структур обычно требуется, чтобы размеры системы превышали некоторое критическое значение - сложную функцию параметров, описывающих реакционно-диффузионные процессы. Мы можем по этому утверждать, что химические неустойчивости задают дальнейший порядок, посредством которого система действует как целое.

Если учесть диффузию, то математическая формулировка проблем, связанных с диссипативными структурами, потребует изучении дифференциальных уравнений в частных производных. Действительно, эволюция концентрации компонент Х со временем определяется уравнением вида 

 

        (2.4)

 

где первый член дает вклад химических реакций в изменении концентрации Х_i и обычно имеет простой полиноминальный вид, а второй член означает диффузию вдоль оси  r.

По истине поразительно, как много разнообразных явлений описывает реакционно-диффузное уравнение (2.4), по этому интересно рассмотреть ² основное решение ², которое бы соответствовала термодинамической ветви. Другие решения можно было бы получать при последовательных не устойчивостях, возникающих по мере удаления от состояния равновесия. Неустойчивости такого типа удобно изучать методами теории бифуркации [ Николис и Пригожин, 1977]. В принципе, бифуркация есть нечто иное, как возникновение при некотором критическом значении параметра нового решения уравнений. Предположим, что мы имеем химическую реакцию, соответствующую кинетическому уравнению [ Маклейн и Уолис, 1974].

                            d X

                             ¾ = a X (X-R)         (2.5)

                             d t

Ясно что при R < 0 существует только одно решение, независящее от времени, X = 0. В точке R = 0 происходит бифуркация, и появляется новое решение X = R.

 

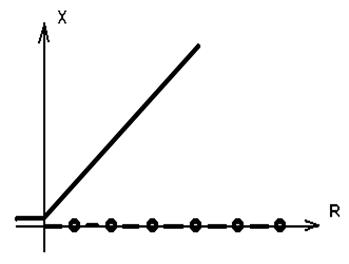
  Рис. 2.3. Бифуркационная диограмма для уравнения (2.5.).

                Сплошная линия соответствует устойчивой ветви,

                точки - неустойчивой ветви.

Анализ устойчивости в линейном приближении позволяет проверить, что решение  X = 0 при переходе через  R = 0 становится неустойчивым, а решение  X = R - устойчивым. В общем случаи при возрастании некоторого характеристического параметра р происходят последовательные бифуркации. На рисунке 2.4. показано единственное решение при  р = р ₁, но при 

 р = р ₂ единственность уступает место множественным решения.

Интересно отметить, что бифуркация в некотором смысле вводит в физику и в химию, историю - элемент, который прежде считался прерогативой наук занимающихся изучением биологическим, общественных и культурных явлений.

 

    Рис. 2.4. Последовательные бифуркации:

                    А и А ¹ - точки первичных бифуркаций из

                    термодинамической ветви,

                    В и В ¹ - точки вторичной бифуркации.

Известно, что при изменении управляющих параметров в системе наблюдаются разнообразные переходные явления. Выделим теперь из этих наблюдений определенные общие черты, характерные для большого числа других переходов в физико химических системах.

С этой целью представим графически (рис. 2.5) зависимость вертикальной компоненты скорости течения жидкости в некоторой определенной точке от внешнего ограничения, или, в более общем виде, зависимость переменной состояние системы Х (или х = Х - Х_s) от управляющего параметра l. Таким образом мы получим график, известный под названием бифуркационной диаграммы.

 

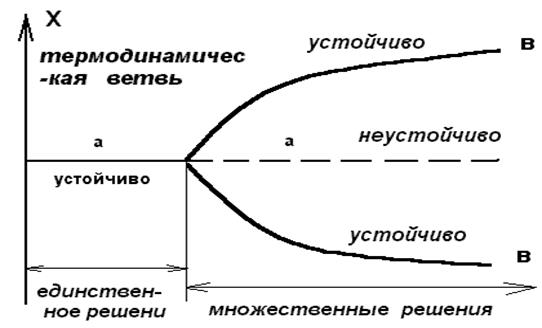
Рис. 2.5. Бифуркационная диаграмма:

        а - устойчивая часть термодинамической ветви,

         а¹ - не устойчивая часть термодинамической ветви,

         в₁,в₂ - диссипативные структуры, рожденные в

                  сверхкритической области.

При малых значения l возможно лишь одно решение, соответствующее состоянию покоя в бенаровском эксперименте.Оно представляет собой непосредственную экстрополяцию термодинамического равновесия, и подобно равновесно, характеризующейся важным свойством - асимптотической устойчивостью, поскольку в этой области система способна гасить внутренние флуктуации или внешнее возмущения. По этой причине такую ветвь состояний мы будем называть термодинамической ветвью. При переходе критического значения параметра l, обозначенного l_c на рисунке 2.5., состоящие на этой ветви становится неустойчивыми, так как флуктуации или малые внешние возмущение уже не гасятся. Действуя подобно усилителю, система отклоняется от стационарного состояния и переходит к новому режиму, в случае бенаровского эксперимента соответствующему состоянию стационарной конвекции. Оба этих режима сливаются при l = l_c и различаются при l > l_c. Это явление называется бифуркацией. Легко понять причины, по которым это явление следует ассоциировать с катастрофическими изменениями и конфликтами. В самом деле, в решающий момент перехода система должна совершить критический выбор (в окрестности l = l_c), что в задаче Бенара связано с возникновением право- или левовращательных ячеек в определенной области пространства (рис. 2.5., ветви в₁ или в₂).

В близи равновесного состояния стационарное состояние асимптотических устойчивы (по теореме о минимальном производстве энтропии), по этому в силу непрерывности эта термодинамическая ветвь простирается во всей докритической области. При достижении критического значения термодинамическая ветвь может стать неустойчивой, так что любое, даже малое возмущение, переводит систему с термодинамической ветви в новое устойчивое состояние, которое может быть упорядоченным. Итак, при критическом значении параметром произошла бифуркация и возникла новая ветвь решений и, соответственно, новое состояние. В критической области, таким образом, событие развивается по такой схеме:

             Флуктуация ® Бифуркация ®

             неравновесный фазовый переход ®

             Рождение упорядоченной структуры.

  Бифуркация в широком понимании - приобретении нового качества движениями динамической системы при малом изменении ее параметров (возникновение при некотором критическом значении параметра нового решения уравнений). Отметим, что при бифуркации выбор следующего состояния носит сугубо случайный характер, так что переход от одного необходимого устойчивого состояния к другому необходимому устойчивому состоянию проходит через случайное (диалектика необходимого и случайного). Любое описание системы, претерпевающей бифуркацию, включает как детерминистический, так и вероятностный элементы, от бифуркации до бифуркации поведении системы детерминировано, а в окрестности точек бифуркации выбор последующего пути случаен. Проводя аналогию с биологической эволюцией можно сказать, что мутации - это флуктуации, а поиск новой устойчивости играет роль естественного отбора. Бифуркация в некотором смысле вводит в физику и химию элемент историзма - анализ состояния в₁, например, подразумевает знание истории системы, прошедшей бифуркацию.

Общая теория процессов самоорганизации открытых сильно не равновесных системах развивается на основе универсального критерия эволюции Пригожина - Гленсдорфа. Этот критерий является обобщением теоремы Пригожина о минимальном производстве энтропии. Скорость производства энтропии, обусловленная изменением термодинамических сил Х, согласно этому критерию подчиняется условию

 

                              d_x P / t £ 0         (2.6)

 

Это неравенство не зависит не от каких предположений о характере связей между потоками и силами в условиях локального равновесия и носит по этому универсальный характер. В линейной области неравенство (2.6.) переходит в теорему Пригожина о минимальном производстве энтропии. Итак, в неравновестной системе процессы идут так, т.е. система эволюционирует таким образом, что скорость производства энтропии при изменении термодинамических сил уменьшается (или равна нулю в стационарном состоянии).

Упорядоченные структуры, которые рождаются вдали от равновесия, в соответствии с критерием (2.6.) и есть диссипативные структуры.

Эволюция бифуркации и последующей самоорганизации обусловлено, таким образом, соответствующими не равновесными ограничениями.

Эволюция переменных Х будет описываться системой уравнений  

                                (2.7)

 

где функции  F как угодно сложным образом могут зависить от самих переменных Х и их пространственных производных координат r и времени t. Кроме того, эти функции буду зависить от управляющих параметров, т.е. тех изменяющихся характеристик, которые могут сильно изменить систему. На первый взгляд кажется очевидным, что структура функции { F } будет сильно определятся типом соответствующей рассматриваемой системы. Однако, можно выделить некоторые основные универсальные черты, независящие от типа систем.

Решение уравнения (2.7), если нет внешних ограничений, должны соответствовать равновесию при любом виде функции F. Поскольку равновесное состояние стационарно, то

F_i ({X_рав},l_рав) = 0          (2.8)

В более общем случае для неравновесного состояния можно аналогично написать условие

F_i ({X},l) = 0              (2.9)

Эти условия налагают определенные ограничения универсального характера, например, законы эволюции системы должны быть такими, чтобы выполнялось требование положительности температуры или химической концентрации, получаемых как решения соответствующих уравнений.

Другой универсальной чертой является нелинейным. Пусть, например некоторая единственная характеристика системы

Удовлетворяет уравнению

                                       (2.10)

где k - некоторый параметр, l - внешние управляющие ограничения. Тогда стационарное состояние определяется из следующего алгебраического уравнения

                               l - kX = 0         (2.11)

откуда

                               Xs = l / k           (2.12)

В стационарном состоянии, таким образом, значении характеристики, например, концентрации, линейно изменяется в зависимости от значений управляющего ограничения l, и имеется для каждого l единственное состояние Х_s. Совершенно однозначно можно предсказать стационарное значение Х при любом l,если иметь хотя бы два экспериментальных значения Х

(l).Управляющий параметр может, в частности, соответствовать степени удаленности системы от равновесия. Поведение в этом случае системы очень похожи на равновесии даже при наличии сильно неравновесных ограничений.

 

Рис. 2.6. Иллюстрация универсальной черты нелинейности в самоорганизации структур.

Если же стационарное значение характеристики Х не линейно зависит от управляющего ограничения при некоторых значениях, то при одном и том же значении имеется несколько различных решений. Например, при ограничениях система имеет три стационарных решения, рисунок 2.6.в. Такое универсальное отличие от линейного поведения наступает при достижении управляющим параметром некоторого критического значения l - проявляется бифуркация. При этом в нелинейной области небольшое увеличение может привести к неодекватно сильному эффекту - система может совершить скачок на устойчивую ветвь при небольшом изменении вблизи критического значения l, рисунок 2.6.в. Кроме того из состояний на ветви А¹В могут происходить переходы АВ¹ (или наоборот) даже раньше, чем будут достигнуты состояния В или А, если возмущения накладываемые на стационарное состояние, больше значение, соответствующего промежуточной ветви А В. Возмущениями могут служить либо внешнее воздействие либо внутренние флуктуации в самой системе. Таким образом, системе с множественными стационарными состояниями присуще универсально свойствам внутренне возбудимость и изменчивости скачкам.

Выполнение теоремы по минимально производстве энтропии в линейной области, а, как обобщение этой теоремы, выполнение универсального критерия (2.6.) и в линейной, и в нелинейной области гарантируют устойчивость стационарных неравновесных состояний. В области линейности необратимых процессов производство энтропии играет такую же роль, как термодинамические потенциалы в равновесной термодинамике. В нелинейной области величина dP / dt не имеет какого либо общего свойства, однако, величина d_x P/dt удовлетворяет неравенству общего характера (2.6.), которая является обобщением теоремы о минимальном производстве энтропии.

 

Предыдущая1234567Следующая

Поделиться:

Воспользуйтесь поиском по сайту: