 |
Основные теоретические положения
|
|
|
|
МОЛЕКУЛЯРНАЯ ФИЗИКА
И ТЕРМОДИНАМИКА 1
Методические указания
К выполнению лабораторных работ
Для студентов всех специальностей
Всех форм обучения
Одобрено
редакционно-издательским советом
Саратовского государственного
технического университета
Саратов 2006
ВВЕДЕНИЕ
Методические указания к выполнению лабораторных работ состоят из описания пяти лабораторных работ по разделу «Молекулярная физика и термодинамика» курса общей физики:
1. «Определение коэффициента вязкости воздуха капиллярным методом»;
2. «Определение отношения теплоемкостей воздуха при постоянном давлении и объеме резонансным методом»;
3. «Определение теплоемкости твердых тел»;
4. «Определение теплоты парообразования воды»;
5. «Определение молярной массы и плотности газа методом откачки».
Каждая лабораторная работы содержит формулировку цели работы, основные теоретические положения, описание экспериментальной установки и методики измерений, порядок обработки результатов эксперимента и расчета погрешностей.
Выполнение предложенных работ способствует углубленному изучению основных понятий и фундаментальных законов молекулярной физики, а также приобретению навыков экспериментальных исследований в физическом практикуме студентами всех специальностей.
Лабораторная работа 1
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ГАЗОВ
КАПИЛЛЯРНЫМ МЕТОДОМ
Цель работы: изучение явления внутреннего трения воздуха, определение коэффициента внутреннего трения и плотности воздуха, расчет средней скорости теплового движения и длины свободного пробега молекул.
Основные теоретические положения
|
|
|
Явления переноса в жидкостях, твердых телах и газах подчиняются аналогичным дифференциальным уравнениям. Общее уравнение для явлений переноса можно вывести, исходя из положений молекулярно-кинетической теории. При выводе уравнения, описывающего явления переноса, будет использовано понятие градиента. Поясним смысл этого понятия.
Если какая-либо физическая величина 
возрастает в направлении 
, то скорость ее возрастания принято характеризовать отношением изменения этой величины 
к расстоянию 
, на котором это изменение произошло. При этом ось OX располагают в направлении максимального возрастания величины . Модуль градиента величины можно определять по формуле:
. (1.1)
Рассмотрим общий случай. Пусть скалярная величина 
является функцией трех координат 
. Градиентом этой функции называется вектор 
, где символами 
обозначены частные производные по координатам.
Подсчитаем число молекул, проходящих за промежуток времени 
через некоторую воображаемую площадку 
, помещенную в газе. По направлению оси движется 
всех молекул, причем 
в положительном направлении оси и в противоположном. Пусть средняя скорость теплового движения молекул 
, их концентрация 
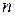. Тогда за время через площадку пройдет всех молекул, находящихся в объеме прямоугольного параллелепипеда с основанием и высотой 
:
. (1.2)
Обозначим переносимую физическую величину . Тогда физическая величина, перенесенная в одном направлении через площадь за время ,
. (1.3)
Такое же количество будет перенесено и в обратном направлении.
Предположим, что газ неоднороден по своим свойствам. Тогда в общем случае можно положить, что в разных местах объема различна и концентрация молекул 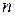и молекулы имеют неодинаковые значения физической величины . Тогда количество величины в единице объема 
будет разным в разных местах объема. Слева от она равна 
, справа – 
. Пусть > , тогда будет иметь место преимущественный перенос физической величины слева направо, и будет перенесено
|
|
|
. (1.4)
Так как изменение физических характеристик частиц происходит только при их столкновении, расстояние, соответствующее разным значениям , должно быть равно 
– средней длине свободного пробега молекул. Средней длиной свободного пробега молекул называется средний путь, проходимый молекулой между столкновениями.
Будем считать, что на расстоянии вправо и влево от значение не менялось, а изменение от до произошло на расстоянии, равном 2 .
Рис 1.1. Перенос величины вдоль оси x
Умножив и поделив выражение (1.4) на 2 , получим:
. (1.5)
Отношение 
представляет собой модуль градиента величины ; расстояние, на котором произошло изменение величины , равное 2 , можно заменить на (
):
. (1.6)
Уравнение переноса запишется в окончательном виде:
. (1.7)
Знак «минус» поставлен в связи с тем, что перенос физической величины происходит в направлении, противоположном ее возрастанию. Градиент направлен справа налево, в направлении возрастания , а перенос происходит слева направо.
В явлении внутреннего трения переносимой физической величиной является импульс молекулы 
, где 
– скорость направленного движения,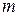 
– масса молекул.
Если концентрация молекул одинакова во всем объеме, то для входящих в уравнение (1.7) величин приращений можно записать: 
и 
.
Согласно второму закону Ньютона изменение импульса равно импульсу действующей силы, то есть 
. В данном случае 
– это сила взаимодействия между слоями газа, действующая в плоскости их соприкосновения, то есть сила внутреннего трения.
Учитывая связь между импульсом тела и силой, преобразуем формулу (1.7) к следующему виду:
. (1.8)
Сокращая это равенство на промежуток времени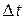 
и учитывая, что плотность газа 
, получаем:
. (1.9)
Обозначим входящее в это выражение произведение трех величин следующим образом:
, (1.10)
тогда для силы получим выражение:
. (1.11)
Таким образом, сила внутреннего трения, возникающая в плоскости соприкосновения двух скользящих относительно друг друга слоев, пропорциональна градиенту скорости и площади соприкосновения слоев.
Формула (1.11) называется законом Ньютона. Величина 
, задаваемая формулой (1.10), называется коэффициентом внутреннего трения (коэффициентом динамической вязкости). Коэффициент вязкости численно равен силе внутреннего трения, возникающей на единице площади при градиенте скорости, равном единице.
|
|
|
|
|
|
