 |
Основные теоретические положения
|
|
|
|
Упругими волнами называются распространяющиеся в упругой среде механические возмущения (деформации). Предположим, что вдоль однородного цилиндрического образца с площадью поперечного сечения 
распространяется упругая продольная волна. Следовательно, по образцу со скоростью 
распространяется относительная деформация 
(рис. 2.1). Выделив некоторую часть образца длиной l, определяем плотность недеформированной среды:
, (2.1)
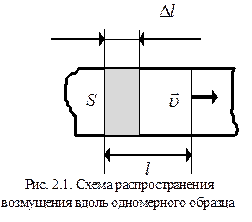Сжатию соответствует увеличение плотности, следовательно, плотность в области сжатия будет равна:
, (2.2)
поскольку площадь поперечного сечения не изменяется, а длина уменьшается.
Преобразуем полученную формулу, умножив и разделив ее на величину 
: 
.
Учитывая, что деформация мала и 
, получим после несложных преобразований:
.
Отсюда, с учетом формулы (2.1), имеем: 
. Обозначим относительную деформацию 
и для изменения плотности запишем:
. (2.3)
Распространение возмущения представляет собой движение области сжатия со скоростью вдоль образца. За промежуток времени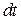 
через поперечное сечение пройдет участок сжатия длиной 
. Масса этого объема газа 
, или, с учетом (2.3), 
.
Объем газа массой dm движется со скоростью и имеет импульс 
. Это изменение импульса объема массой dm по второму закону Ньютона равно произведению действующей на него силы упругости и времени ее действия. Сила упругости определяется законом Гука в следующем виде:
, (2.4)
где 
– напряжение, Е - модуль упругости. Таким образом, 
. Следовательно, 
, откуда получаем формулу для скорости распространения продольной упругой волны:
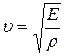. (2.5)
Если упругая волна распространяется в газе, находящемся в гладкой прямолинейной трубе с постоянным поперечным сечением, то, учитывая, что в отличие от твердых тел, газы не оказывают сопротивление сдвигу, в них могут возникать только продольные волны. Следовательно, скорость распространения упругой волны в газе можно вычислить по формуле (2.5). Для этого определим модуль упругости Е для газа.
|
|
|
Если при действии силы F на некоторый объем газа давление в нем возрастет на величину 
по отношению к давлению P в невозмущенном состоянии, то, воспользовавшись законом Гука, записанным в виде формулы (2.4), и умножив числитель и знаменатель этого выражения на площадь образца 
, можно получить:
(2.6)
или 
. (2.7)
Если считать изменения давления и объема 
бесконечно малыми, можно записать:
, (2.8)
где знак «минус» означает, что увеличение давления соответствует уменьшению объема.
Предположим, что в газе распространяется звуковая волна, которая представляет собой упругую волну малой интенсивности, с частотой от 16 до 20000 Гц. Колебания плотности в звуковой волне происходят так быстро, что теплообмен между слоями газа, имеющими различные температуры, не успевает происходить. Поэтому процесс распространения звуковой волны в газе можно считать адиабатным, и к нему можно применить уравнение Пуассона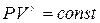 
, дифференцируя которое получаем: 
, откуда
. (2.9)
Из выражений (2.8) и (2.9) найдем:
. (2.10)
Определим Р из уравнения Менделеева-Клапейрона и, учитывая, что плотность газа 
, запишем 
. Подставив эту формулу в уравнение (2.10), имеем:
. (2.11)
Подставив выражение (2.11) в (2.5), получаем формулу Лапласа для расчета скорости звука в газе:
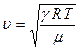, (2.12)
из которой следует:
. (2.13)
Таким образом, для определения отношения теплоемкостей газа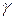 
достаточно измерить его температуру и скорость распространения звука в этом газе.
Скорость звука при данной температуре может быть определена резонансным методом. Во время распространения волны вдоль закрытого канала она многократно отражается от торцов, и звуковые колебания в канале представляют результат наложения этих отраженных волн. Если длина канала L равна целому числу полуволн 
(n - целое число, l - длина волны), то волна, отраженная от торца канала, возвратившись к его началу и снова отражаясь, совпадает по фазе с падающей волной. Такие волны усиливают друг друга, амплитуда колебаний при этом резко возрастает - наступает резонанс. При звуковых колебаниях слои газа, прилегающие к торцам канала, не испытывают смещения. В этих местах образуются узлы смещения, которые повторяются через l/2 по всей длине канала. Между узлами находятся максимумы смещения (пучности).
|
|
|
Скорость звука связана с частотой колебаний n и длиной волны l соотношением 
, с учетом которого условие резонанса можно записать в виде: 
или
, (2.14)
где 
- резонансная частота.
Зависимость резонансной частоты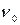 
от номера резонанса n (2.14) может быть проверена экспериментально. Изменяя частоту колебаний при постоянной длине канала, построим график зависимости 
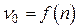, по угловому коэффициенту которого 
определим скорость звука.
|
|
|
