 |
Основные теоретические положения
|
|
|
|
Саратовский государственный технический университет
МОЛЕКУЛЯРНАЯ ФИЗИКА
И ТЕРМОДИНАМИКА 2
Методические указания
К лабораторным работам по физике
Для студентов всех специальностей
Всех форм обучения
Одобрено
редакционно - издательским советом
Саратовского государственного технического университета
Саратов 2006
ВВЕДЕНИЕ
В данных методических указаниях приведены описания четырёх лабораторных работ по молекулярной физике и термодинамике:
1. Определение коэффициента взаимной диффузии воздуха и водяного пара.
2. О пределение коэффициента теплопроводности воздуха методом нагретой нити.
3. О пределение изменения энтропии при нагревании и плавлении олова.
4. Определение отношения теплоёмкостей воздуха при постоянном давлении и объёме.
Описание каждой лабораторной работы содержит следующие разделы:
1. Цель работы.
2. О сновные теоретические положения.
3. Методика эксперимента.
4. Описание экспериментальной установки и порядок выполнения работы.
5. Обработка результатов измерений.
Последний раздел имеет исключительно важное значение, поскольку инженер должен не только представлять себе основные теоретические положения, касающиеся того или иного физического явления и проводить необходимые измерения, но и правильно обработать результаты эксперимента. В настоящих методических указаниях в приложении приведено краткое описание основных методик расчёта погрешностей, необходимых при выполнении предлагаемых лабораторных работ.
Лабораторная работа 1
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЗАИМНОЙ ДИФФУЗИИ ВОЗДУХА И ВОДЯНОГО ПАРА
|
|
|
Цель работы: изучение явления диффузии в газах, экспериментальное определение коэффициента взаимной диффузии воздуха и водяного пара по скорости испарения жидкости в капилляре.
Основные теоретические положения
Диффузией называется явление проникновения двух или нескольких соприкасающихся веществ друг в друга. Диффузия сопровождается переносом массы диффундирующего вещества.
Рассмотрим явление диффузии в газах. Перенос массы связан с тепловым движением молекул. Скорости теплового движения молекул велики (они составляют сотни метров в секунду при комнатной температуре), и, казалось бы, диффузия должна происходить быстро. Однако, как показывает опыт, диффузия в газах довольно медленный процесс и может происходить сутками.
Причина этого несоответствия заключается в том, что, благодаря малой длине свободного пробега, молекулы непрерывно сталкиваются друг с другом. Поэтому молекула за одну секунду уходит на очень небольшое расстояние от того места, где она находилась. Для того, чтобы попасть из одной точки в другую, молекулы проходят длинный зигзагообразный путь, во много раз превосходящий расстояние по прямой между этими точками. Таким образом, молекулы газа не столько движутся вперед, сколько «толкутся» на одном месте. Следовательно, в газах механизмом, обеспечивающим явление диффузии, является столкновение молекул.
Опыт показывает, что при диффузии через некоторую площадку 
переносится тем большая масса газа 
, чем больше размеры площадки , чем за больший промежуток времени 
наблюдается диффузия и чем скорее меняется в направлении, перпендикулярном к площадке , плотность диффундирующего газа 
(рис. 1.1):
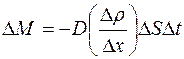. (1.1)
Величина 
характеризует изменение плотности газа на единице длины в направлении оси 
; она называется градиентом плотности. Коэффициент 
называется коэффициентом диффузии газа. Он зависит от сорта газа и условий, при которых газ находится.
|
|
|
В газах различают самодиффузию, взаимную (концентрационную) диффузию и термодиффузию.
Самодиффузия − это диффузия молекул газа в среде того же газа. С явлением самодиффузии мы имеем дело, например, когда газовая смесь состоит из двух изотопов одного и того же вещества. Изотопы незначительно отличаются друг от друга массой, но не отличаются никакими другими свойствами. Явление самодиффузии можно наблюдать также в смеси газов, где часть молекул заменена другими по химическому составу молекулами, но имеющими почти такие же размеры и массу (например,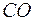 
и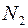 
).
Рассмотрим явление самодиффузии с точки зрения молекулярно-кинетической теории.
Рис. 1.1. Перенос молекул через площадку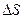 
.
Так как молекулы одного и того же газа одинаковы, то для изучения процесса самодиффузии пометим часть молекул.
Допустим, что концентрации меченых молекул по обе стороны от площадки (рис. 1.1) не одинаковы. Тогда меченые и немеченые молекулы, хаотически двигаясь, будут переходить через эту площадку в ту и другую сторону. Результирующий поток меченых молекул будет направлен оттуда, где их концентрация больше, туда, где она меньше. Тоже самое справедливо и для немеченых молекул, только их результирующий поток противоположен потоку меченых.
Мысленно выделим справа и слева от площадки на расстояниях от нее, равных средней длине свободного пробега 
, одинаковые кубические объемы 
и 
. Пусть боковые грани кубиков и параллельны площадке и равны ей по величине. Длину ребра кубиков обозначим через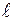 
; 
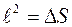. Обозначим число меченых молекул в кубике через 
. Ввиду полной беспорядочности движения молекул газа, можно считать, что 
этих молекул движется вдоль оси , из них 
− в положительном направлении (т.е. к площадке ), а − в отрицательном направлении оси . Так как площадка отстоит на расстоянии от кубика А, то все молекулы долетят до нее без столкновений и пролетят через . Время 
, за которое 
молекул пролетят через :
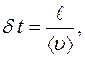
где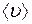 
− средняя арифметическая скорость молекул.
Таким образом, число меченых молекул 
, пролетающих через площадку за единицу времени слева направо, равно:
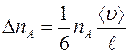. (1.2)
Обозначим через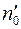 
число меченых молекул в единице объема в том месте, где находится кубик ; тогда 
и
|
|
|
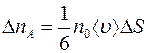(1.3)
Точно также получим, что число меченых молекул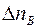 
, пролетающих через площадку в единицу времени справа налево, будет равно:
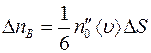, (1.4)
где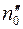 
– число меченых молекул в единице объема в том месте, где находится кубик .
Отсюда разность между числом меченых молекул, пролетающих через слева направо и справа налево за некоторый произвольный промежуток времени , равна:
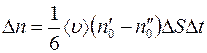. (1.5)
Массу , переносимую через за время мечеными молекулами, получим, умножив число 
этих молекул на массу одной молекулы 
:
. (1.6)
Разность 
представляем в виде:
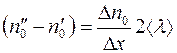. (1.7)
Тогда
, (1.8)
но 
и, следовательно,
. (1.9)
Сравнивая выражение (1.9) с формулой (1.1) получим:
. (1.10)
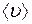Таким образом, коэффициент диффузии связан со средней длиной свободного пробега и средней скоростью движения молекул.
Средняя скорость движения молекул 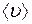пропорциональна 
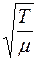, где 
– абсолютная температура, 
– молярная масса газа, а при постоянной плотности газа от его температуры не зависит. Отсюда следует, что для данного газа, при нагревании его при постоянном объеме, коэффициент диффузии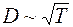 
.
Средняя длина свободного пробега обратно пропорциональна давлению газа и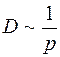 
. Здесь 
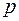– суммарное давление смеси газов.
В разреженных газах диффузия происходит быстрее, чем в газах при больших давлениях.
Подставляя в (10) выражение для : 
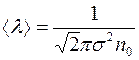, получим:
. (1.11)
Следовательно, коэффициент диффузии оказывается непосредственно связанным с эффективным диаметром молекул 
.
Величина коэффициента самодиффузии для того или иного газа при данной температуре и давлении не зависит ни от того, какую часть молекул мы пометили, ни от того, метили ли мы молекулы вообще. Этот коэффициент является характеристикой теплового движения молекул.
Отношение 
называется диффузионным потоком, а величина 
– удельным диффузионным потоком.
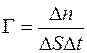. (1.12)
Согласно формулам (1.5) и (1.10),
. (1.13)
Соотношение (1.13) называется законом Фика.
Рассмотрим взаимную диффузию газов. Если в смеси двух различных газов 1 и 2, находящейся при постоянной температуре и постоянном давлении, компоненты смеси 1 и 2 распределены неравномерно, то начнется взаимная диффузия газов и в конце концов установится равномерное распределение молекул смеси по всему объему. Взаимная диффузия иначе называется концентрационной.
|
|
|
Если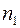 
– число молекул газа 1, а 
– число молекул газа 2 в единичном объеме смеси и если градиенты концентраций 
и 
направлены вдоль оси , то удельные диффузионные потоки 
и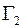 
молекул газов 1 и 2 выразятся следующими равенствами:
;
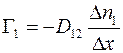(1.14)
,
где 
– коэффициент диффузии газа 1 в газ 2;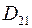 
– коэффициент диффузии газа 2 в газ 1.
Если температура и давление в смеси всюду постоянны, то общее число молекул в единичном объеме также всюду постоянно, т.е.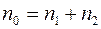 
. Следовательно
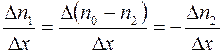. (1.15)
При этих условиях удельные диффузионные потоки молекул газа 1 и газа 2 также должны быть равными по величине, но противоположными по направлениям:
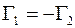. (1.16)
Из соотношений (1.14) – (1.16) следует, что
. (1.17)
При взаимной диффузии газов существенно одинаковые или разные молекулы сталкиваются друг с другом, перед тем как пройти через сечение , через которое осуществляется перенос массы газа. Диффузионный поток и коэффициент диффузии (1.17) обусловлены столкновениями разнородных молекул и не зависят от столкновений одинаковых молекул. Учет этого обстоятельства, основанный на понятии длины свободного пробега очень сложен. Приходится пользоваться двумя средними длинами свободного пробега (для газов 1 и 2), а между тем результаты плохо согласуются с экспериментом. Лучшие результаты дает теория, в которой понятие длины свободного пробега не используется. Эта теория для коэффициента диффузии дает следующее соотношение:
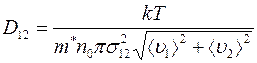, (1.18)
где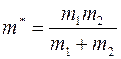 
; 
– масса молекулы 1-го газа, 
– масса молекулы 2-го газа;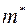 
называется приведенной массой молекул газов 1 и 2.
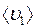и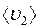 
– средние скорости молекул газов 1 и 2 соответственно; 
– эффективный диаметр столкновения разнородных молекул, который можно считать равным среднему диаметру молекул 1 и 2:
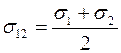
Отметим, что согласно выражению (1.18) коэффициент взаимной диффузии газов не зависит от концентраций компонент смес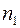и и . Этот вывод подтверждается опытом.
Диффузия может порождаться не только разницей концентраций компонент смеси двух газов, но и другими причинами. Одной из таких причин является неодинаковость температуры в разных частях объема смеси.
Заполним однородной смесью двух газов два сосуда, расположенных друг над другом и соединенных трубкой. Если верхний сосуд нагревать, а нижний охлаждать, то молекулы тяжелого газа обычно (но не всегда) диффундируют в направлении потока теплоты, а молекулы легкого газа – в обратном направлении. В результате произойдет частичное разделение компонент первоначально однородной смеси. Это явление называется тепловой (термической) диффузией.
|
|
|
Возникшее разделение компонент смеси приведет к взаимной диффузии, стремящейся устранить неоднородность концентраций различных газов смеси. Следовательно, эти два эффекта – термодиффузия и взаимная диффузия – действуют противоположным образом.
Если разность температур на концах сосудов, содержащих смесь газов, поддерживать постоянной, то установится стационарное состояние, при котором перенос молекул путем взаимной диффузии уравновешивается переносом их путем термодиффузии.
По своей природе термодиффузия отличается от самодиффузии и взаимной диффузии, которые обуславливались самим фактом столкновения молекул между собой. Термодиффузия обуславливается не самим фактом столкновения молекул, а зависимостью частоты столкновений между молекулами от их скорости. Коэффициент термодиффузии зависит от взаимодействия между разнородными молекулами. Если представить силы отталкивания между молекулами в ви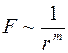де 
, где 
– расстояние между молекулами, то расчет показывает, что при 
термодиффузия отсутствует. При 
термодиффузия происходит так, что более горячие области обогащаются более легкой компонентой смеси, а при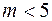 
– более тяжелой. Следовательно, измеряя коэффициент термодиффузии, можно получить информацию о природе межмолекулярных сил.
Термодиффузия получила важное применение для разделения изотопов. Ввиду близости масс изотопов обогащение состава смеси одним из изотопов при разумных градиентах температур невелико. Для значительного разделения изотопов используется многоступенчатый процесс, при котором на каждом последующем этапе обогащения в качестве исходной смеси берется смесь, обогащенная на предыдущем этапе.
Полная теория термодиффузии является очень сложной и обсуждается в специализированной литературе по диффузии.
Методика эксперимента
Для определения коэффициента взаимной диффузии воздуха и водяного пара рассмотрим частично заполненную водой узкую трубку постоянного сечения S (капилляр), открытую с одного конца. Ось OX направим вдоль оси капилляра. На границе с водой (x=0) парциальное давление водяного пара pп в трубке равняется давлению насыщенного пара pн при температуре опыта. Давление водяного пара в капилляре меняется вдоль оси OX от значения pн до давления p1 около открытого конца капилляра. Давление p1 определяется влажностью воздуха в лаборатории. Таким образом, если предположить, что на расстоянии dx вдоль оси трубки давление водяного пара меняется на dpп, то градиент парциального давления пара равен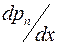 
, и в трубке возникает диффузионный поток пара 
, направленный вверх.
Масса пара, которая переносится через площадь поперечного сечения капилляра за одну секунду, согласно формулам (1.9) и (1.10), равна:
. (1.19).
Плотность пара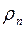 
можно выразить через его парциальное давление, используя уравнение состояния идеального газа, следующим образом:
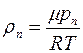, (1.20)
здесь – молярная масса воды, 
– универсальная газовая постоянная.
Подставляя (1.20) в формулу (1.19), получим6
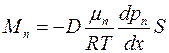. (1.21)
С другой стороны, массу пара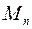 
можно выразить через скорость понижения жидкости в капилляре:
, (1.22)
где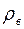 
– плотность воды, а 
– понижение уровня жидкости в капилляре за время 
.
Подставляя соотношение (1.22) в уравнение (1.21), получим
.
Интегрируя последнее равенство, получим:
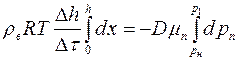
или
,
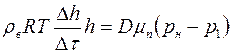откуда найдём коэффициент взаимной диффузии :
, (1.23)
где 
– расстояние от поверхности воды до верхнего края капилляра. Формулу (1.23) можно использовать для экспериментального определения коэффициента взаимной диффузии воздуха и водяного пара.
|
|
|
