 |
Квантовая яма, квантовый барьер. Уровни размерного квантования.
|
|
|
|
Квантовые ямы. Этим термином обозначаются системы, в которых имеется размерное квантование движения носителей заряда в одном направлении ( квантовая структура, в которой движение электрона ограничено в одном направлении ).
Квантовая яма - это мезоскопический объект, характеризующийся потенциальной ямой для подвижных носителей заряда – электронов и дырок, которая ограничивает подвижность частиц с трех до двух измерений, тем самым заставляя их двигаться в плоском слое. Квантово-размерные эффекты проявляют себя когда длина ямы становится сравнима с длиной волны де Бройля частиц (обычно электронов или дырок), и приводят к появлению энергетических минизон.
Энергию дна каждой из минизон можно приблизительно оценить с помощью выражения: 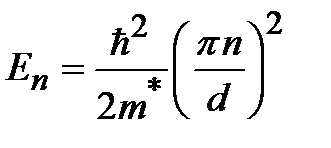 , где
, где 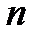 - номер минизоны,
- номер минизоны,  - эффективная масса соответствующей квазичастицы, - ширина квантовой ямы.
- эффективная масса соответствующей квазичастицы, - ширина квантовой ямы.
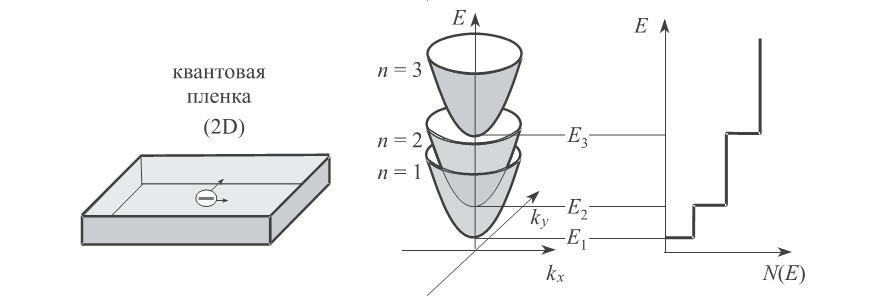
Рисунок 3. Квантовая яма (квантовая плёнка): дисперсионная зависимость и плотность состояний 
Основные физические явления в квантовых ямах: размерное квантование электронного спектра, квантовый эффект Холла (целочисленный и дробный), при специальном приготовлении очень высокая подвижность электронов. Основные методы получения квантовых ям на гетероструктурах: металлоорганическая газовая эпитаксия и молекулярно-пучковая эпитаксия (эпитаксия — метод выращивания кристаллов на поверхности подложки).
Структуры с туннельно-прозрачными барьерами (системы квантовых ям и сверхрешетки). Основные физические явления в таких системах: резонансное туннелирование; формирование минизонного спектра в сверхрешетках ‑ периодических системах, содержащих много квантовых ям, разделенных туннельно-прозрачными барьерами; нелинейные электрические и оптические явления в сверхрешетках. Методы выращивания этих структур те же, что и для квантовых ям.
|
|
|

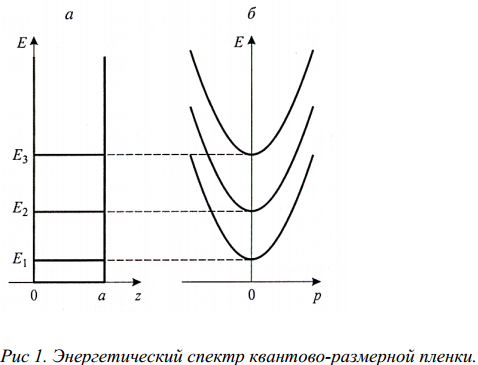
Рассмотрим основную идею размерного квантования на примере электронов, находящихся в очень тонкой металлической или полупроводниковой пленке толщиной а. То обстоятельство, что в обычных условиях носители сосредоточены в пленке и не выходят из нее в окружающую среду, означает, что материал пленки (металл или полупроводник) представляет собой потенциальную яму для электронов глубиной, равной работе выхода W, и шириной а. Согласно законам квантовой механики, энергия электронов в такой яме квантуется, т.е. может принимать лишь некоторые дискретные значения Еn, где n имеет целочисленные значения 1,2,3,…. Эти дискретные значения называют уровнями размерного квантования. Типичные значения работы выхода в большинстве твердых тел имеют величину W = 4-5 эВ, на несколько порядков превышающую характерную тепловую энергию носителей kТ, равную при комнатной температуре 0.026 эВ. Поэтому потенциальную яму можно считать бесконечно глубокой (рис.1 а). Если пленка занимает область 0<z<а, то в этом случае энергетические уровни квантовых состояний выглядят следующим образом:
 (1)
(1)
где m- эффективная масса электрона. Другим необходимым условием, позволяющим считать яму бесконечно глубокой, является малость значений Еn, по сравнению с ее действительной глубиной W. Это условие, которое для нижних уровней можно записать в виде  , при
, при 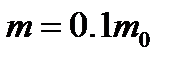 соответствует толщинам пленки порядка нескольких межатомных расстояний. Во всех реальных структурах это условие соблюдается.
соответствует толщинам пленки порядка нескольких межатомных расстояний. Во всех реальных структурах это условие соблюдается.
Для свободной частицы с эффективной массой, движение которой в кристалле в направлении ограничено непроницаемыми барьерами (т.е. барьерами с бесконечной потенциальной энергией), разрешенные значения волновых векторов блоховских волн имеют вид:
|
|
|
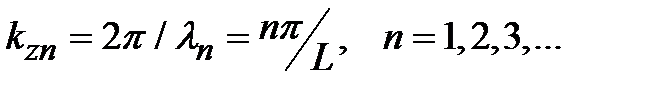 (1)
(1)
а энергия основного состояния по сравнению с состоянием без ограничения возрастает на величину
 (2)
(2)
Это увеличение энергии называется энергией размерного квантования частицы. Энергия размерного квантования является следствием принципа неопределенности в квантовой механике. Соответствующее увеличение кинетической энергии частицы дается тогда выражением (2). Поэтому данный эффект часто называют квантовым размерным эффектом.
Кроме увеличения минимальной энергии частицы квантовый размерный эффект приводит также к квантованию энергий ее возбужденных состояний. Так для бесконечного одномерного потенциала «прямоугольной ямы» энергии возбужденных состояний выражаются как 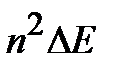 где
где  .
.
|
|
|


