Резонансное туннелирование. Резонансно-туннельный диод.
Когда область, в которую или из которой может происходить туннельный переход электрона, является квантово-размерной (квантовая плоскость, квантовая линия, квантовая точка), то наблюдается еще один интересный эффект – " резонансное туннелирование ". Чтобы объяснить его физическую сущность, рассмотрим снова двойной туннельный барьер (ДТБ), в котором промежуточный слой между двумя туннельными переходами является квантовой плоскостью. На рис. 3.8 слева показаны соответствующие энергетические диаграммы. Вдоль вертикали отложена энергия электронов, вдоль горизонтали – координата. Цифрами 1 и 5 на последней обозначены внешние области, к которым прикладывается напряжение: 1 – катод, 5 – анод;  и
и 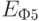 – энергетические уровни Ферми в них. Цифрами 2 и 4 обозначены туннельные барьеры, цифрой 3 – квантово-размерная область.
– энергетические уровни Ферми в них. Цифрами 2 и 4 обозначены туннельные барьеры, цифрой 3 – квантово-размерная область.
Как мы уже отмечали выше, в такой области значения энергии электрона квантованы. Через 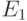 и
и 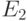 обозначены разрешенные в этой области энергетические уровни. В диапазоне энергий, который здесь рассматривается, в этих областях нет разрешенных энергетических уровней для электронов.
обозначены разрешенные в этой области энергетические уровни. В диапазоне энергий, который здесь рассматривается, в этих областях нет разрешенных энергетических уровней для электронов.
Обозначим разности между разрешенными в квантово-размерной области энергетическими уровнями 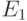 и
и 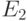 и энергетическим уровнем Ферми
и энергетическим уровнем Ферми  через
через

Напомним, что при туннельном переходе энергия электрона не изменяется. Примем во внимание также то, что электрическое напряжение 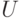 , приложенное между анодом и катодом, падает в основном на туннельных барьерах 2 и 4 и распределяется между ними примерно поровну. Потенциальная энергия электронов в области анода 5 уменьшается на величину
, приложенное между анодом и катодом, падает в основном на туннельных барьерах 2 и 4 и распределяется между ними примерно поровну. Потенциальная энергия электронов в области анода 5 уменьшается на величину 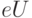 , вследствие чего все энергетические уровни смещаются вниз. В квантово-размерной области 3 потенциальная энергия электронов уменьшается на величину
, вследствие чего все энергетические уровни смещаются вниз. В квантово-размерной области 3 потенциальная энергия электронов уменьшается на величину  , и на такую же величину смещаются вниз разрешенные энергетические уровни
, и на такую же величину смещаются вниз разрешенные энергетические уровни 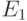 и
и 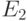 .
.
Верхняя энергетическая диаграмма (рис. 3.8.а) соответствует случаю, когда  . Для большинства электронов из области 1, которые находятся вблизи уровня Ферми
. Для большинства электронов из области 1, которые находятся вблизи уровня Ферми  , в области 3 не находится разрешенного энергетического уровня. И потому их туннельный переход сквозь барьер 2 не происходит. Пройти сквозь этот барьер из области 1 могут лишь электроны с энергией на
, в области 3 не находится разрешенного энергетического уровня. И потому их туннельный переход сквозь барьер 2 не происходит. Пройти сквозь этот барьер из области 1 могут лишь электроны с энергией на  выше уровня Ферми, а таких электронов мало. Туннельный ток незначителен.
выше уровня Ферми, а таких электронов мало. Туннельный ток незначителен.
Когда же напряжение между анодом 5 и катодом 1 возрастает до величины, при которой  , тогда уже значительная часть электронов с энергиями близ уровня Ферми
, тогда уже значительная часть электронов с энергиями близ уровня Ферми  имеет возможность пройти сквозь туннельный барьер 2. И электрический ток сквозь структуру резко возрастает, достигая максимума при
имеет возможность пройти сквозь туннельный барьер 2. И электрический ток сквозь структуру резко возрастает, достигая максимума при 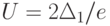 . Типичная вольтамперная характеристика структуры показана на рис. 3.8.г. Когда напряжение превышает указанную величину, то для большинства электронов из области 1 снова не находится разрешенного энергетического уровня в области 3, и они не могут пройти в эту область. Туннельный ток сквозь структуру уменьшается (рис. 3.8.в). И лишь когда напряжение начинает приближаться к величине
. Типичная вольтамперная характеристика структуры показана на рис. 3.8.г. Когда напряжение превышает указанную величину, то для большинства электронов из области 1 снова не находится разрешенного энергетического уровня в области 3, и они не могут пройти в эту область. Туннельный ток сквозь структуру уменьшается (рис. 3.8.в). И лишь когда напряжение начинает приближаться к величине 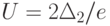 , у некоторых электронов из области 1 появляется возможность перейти на разрешенный энергетический уровень
, у некоторых электронов из области 1 появляется возможность перейти на разрешенный энергетический уровень 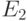 . И тогда туннельный ток сквозь структуру снова начинает расти.
. И тогда туннельный ток сквозь структуру снова начинает расти.
(примечение: я ничего не понимаю)
Описанное явление резкого возрастания электрического тока сквозь туннельный переход, когда энергетические уровни электронов с обеих сторон от перехода уравниваются, называют " резонансным туннелированием " (англ. resonant tunneling).
Решение квантовомеханической задачи прохождения электронов с энергией  сквозь два барьера высотой
сквозь два барьера высотой 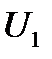 и
и 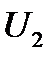 , разделенных расстоянием
, разделенных расстоянием 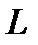 , шириной
, шириной 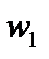 и
и  , показанную на рис. 1, позволяет найти коэффициент прохождения
, показанную на рис. 1, позволяет найти коэффициент прохождения 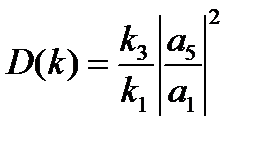 .
.
Соответствующие уровни энергии 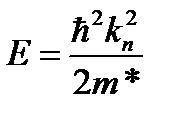 называются резонансными уровнями квантовой ямы, разделяющей барьеры.
называются резонансными уровнями квантовой ямы, разделяющей барьеры.
Соотношение для уровней изолированной ямы, когда система резонансных уровней практически не зависит от толщины барьера: 
Воспользуйтесь поиском по сайту:


 и
и 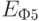 – энергетические уровни Ферми в них. Цифрами 2 и 4 обозначены туннельные барьеры, цифрой 3 – квантово-размерная область.
– энергетические уровни Ферми в них. Цифрами 2 и 4 обозначены туннельные барьеры, цифрой 3 – квантово-размерная область.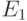 и
и 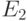 обозначены разрешенные в этой области энергетические уровни. В диапазоне энергий, который здесь рассматривается, в этих областях нет разрешенных энергетических уровней для электронов.
обозначены разрешенные в этой области энергетические уровни. В диапазоне энергий, который здесь рассматривается, в этих областях нет разрешенных энергетических уровней для электронов.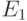 и
и 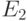 и энергетическим уровнем Ферми
и энергетическим уровнем Ферми  через
через
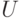 , приложенное между анодом и катодом, падает в основном на туннельных барьерах 2 и 4 и распределяется между ними примерно поровну. Потенциальная энергия электронов в области анода 5 уменьшается на величину
, приложенное между анодом и катодом, падает в основном на туннельных барьерах 2 и 4 и распределяется между ними примерно поровну. Потенциальная энергия электронов в области анода 5 уменьшается на величину 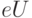 , вследствие чего все энергетические уровни смещаются вниз. В квантово-размерной области 3 потенциальная энергия электронов уменьшается на величину
, вследствие чего все энергетические уровни смещаются вниз. В квантово-размерной области 3 потенциальная энергия электронов уменьшается на величину  , и на такую же величину смещаются вниз разрешенные энергетические уровни
, и на такую же величину смещаются вниз разрешенные энергетические уровни 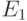 и
и 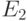 .
. . Для большинства электронов из области 1, которые находятся вблизи уровня Ферми
. Для большинства электронов из области 1, которые находятся вблизи уровня Ферми  , в области 3 не находится разрешенного энергетического уровня. И потому их туннельный переход сквозь барьер 2 не происходит. Пройти сквозь этот барьер из области 1 могут лишь электроны с энергией на
, в области 3 не находится разрешенного энергетического уровня. И потому их туннельный переход сквозь барьер 2 не происходит. Пройти сквозь этот барьер из области 1 могут лишь электроны с энергией на  выше уровня Ферми, а таких электронов мало. Туннельный ток незначителен.
выше уровня Ферми, а таких электронов мало. Туннельный ток незначителен. , тогда уже значительная часть электронов с энергиями близ уровня Ферми
, тогда уже значительная часть электронов с энергиями близ уровня Ферми  имеет возможность пройти сквозь туннельный барьер 2. И электрический ток сквозь структуру резко возрастает, достигая максимума при
имеет возможность пройти сквозь туннельный барьер 2. И электрический ток сквозь структуру резко возрастает, достигая максимума при 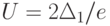 . Типичная вольтамперная характеристика структуры показана на рис. 3.8.г. Когда напряжение превышает указанную величину, то для большинства электронов из области 1 снова не находится разрешенного энергетического уровня в области 3, и они не могут пройти в эту область. Туннельный ток сквозь структуру уменьшается (рис. 3.8.в). И лишь когда напряжение начинает приближаться к величине
. Типичная вольтамперная характеристика структуры показана на рис. 3.8.г. Когда напряжение превышает указанную величину, то для большинства электронов из области 1 снова не находится разрешенного энергетического уровня в области 3, и они не могут пройти в эту область. Туннельный ток сквозь структуру уменьшается (рис. 3.8.в). И лишь когда напряжение начинает приближаться к величине 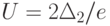 , у некоторых электронов из области 1 появляется возможность перейти на разрешенный энергетический уровень
, у некоторых электронов из области 1 появляется возможность перейти на разрешенный энергетический уровень 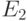 . И тогда туннельный ток сквозь структуру снова начинает расти.
. И тогда туннельный ток сквозь структуру снова начинает расти. сквозь два барьера высотой
сквозь два барьера высотой 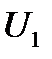 и
и 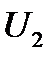 , разделенных расстоянием
, разделенных расстоянием 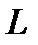 , шириной
, шириной 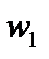 и
и  , показанную на рис. 1, позволяет найти коэффициент прохождения
, показанную на рис. 1, позволяет найти коэффициент прохождения 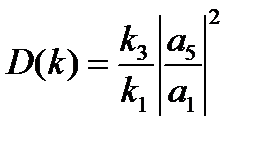 .
.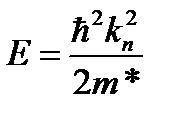 называются резонансными уровнями квантовой ямы, разделяющей барьеры.
называются резонансными уровнями квантовой ямы, разделяющей барьеры.


