 |
Свойства двумерного электронного газа
|
|
|
|
Обычно в объемном полупроводнике энергия электронов непрерывна, ее можно сравнить с энергией свободного электрона с волновым вектором k, но с эффективной массой m*:

Если мы ограничим трехмерный электронный газ в одном из направлений (обычно это принимают за направление z), то в этом случае движение в плоскости, перпендикулярной оси z остается свободным, и энергия электрона может принимать любые значения, а вот вдоль оси z энергия электрона может иметь лишь некие фиксированные значения En. Тогда полная энергия будет иметь вид:
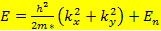 , где n = 0, 1, 2…,
, где n = 0, 1, 2…,
Номер n называется номером подзоны размерного квантования. Если электроны находятся только в самой нижней (нулевой) подзоне (т. е. энергия вдоль оси z для всех двумерных электронов равна 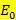 ), то говорят о двумерном электронном газе.
), то говорят о двумерном электронном газе.
Если заполнено несколько подзон, то о квазидвумерном.
Также необходимо сказать о концентрации двумерного электронного газа: В отличие от трехмерного случая, концентрация определяется как число носителей заряда, приходящихся на единицу объема. Она имеет размерность 1/ 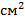
В обычном эффекте Холла в двумерном электронном газе формула для холловского сопротивления будет иметь вид 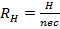 , где n-уже двумерная концентрация.
, где n-уже двумерная концентрация.
Согласно законам квантовой механики, частицы, совершающие периодическое движение, могут обладать лишь дискретными значениями. Поэтому у заряженных частиц в магнитном поле появляются уровни энергии, называемые уровнями Ландау.
На каждом уровне Ландау может находиться (т.е. электроны будут иметь одну и ту же энергию) лишь определенное число электронов (на единицу площади образца). Это число называется кратностью вырождения, оно не зависит от номера уровня Ландау, от эффективной массы электрона, а определяется лишь мировыми константами и величиной магнитного поля. Эта величина равна  , получить которую можно из простых соображений, рассматривая электрон как классическую частицу, двигающуюся по окружности.
, получить которую можно из простых соображений, рассматривая электрон как классическую частицу, двигающуюся по окружности.
|
|
|
Отношение  , где n — концентрация двумерного газа, называется фактором заполнения, оно показывает, сколько уровней Ландау заполнено электронами при данной концентрации в заданном магнитном поле. Целый фактор заполнения означает, что какое-то число уровней Ландау полностью заполнено, а следующие (вышележащие) уровни пусты.
, где n — концентрация двумерного газа, называется фактором заполнения, оно показывает, сколько уровней Ландау заполнено электронами при данной концентрации в заданном магнитном поле. Целый фактор заполнения означает, что какое-то число уровней Ландау полностью заполнено, а следующие (вышележащие) уровни пусты.
КВАНТОВЫЙ ЭФФЕКТ ХОЛЛА.
В двумерном электронном слое зависимости  от Н и n перестают быть плавными. Возникают особые значения сопротивлений, не изменяющиеся при изменении Н и n в довольно широком диапазоне. При этом значения RH в этих областях выражаются лишь фундаментальными постоянными и целым числом i:
от Н и n перестают быть плавными. Возникают особые значения сопротивлений, не изменяющиеся при изменении Н и n в довольно широком диапазоне. При этом значения RH в этих областях выражаются лишь фундаментальными постоянными и целым числом i: 
Продольное же сопротивление 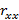 (отношение падения напряжения вдоль направления тока к величине этого тока) в этих условиях обращается в нуль.
(отношение падения напряжения вдоль направления тока к величине этого тока) в этих условиях обращается в нуль.
При рассеянии изменяется направление скорости электрона, т. е. изменяется его вклад в ток.
Если на уровне Ландау есть свободные места (т. е. уровень Ландау заполнен частично), то такое рассеяние возможно в пределах одного энергетического уровня без существенного изменения энергии электрона. Другое дело, если уровень Ландау заполнен полностью. В этом случае все места на нем заняты, и электрон не может изменить своего положения относительно других электронов. Единственная возможность изменить импульс в этом случае — это перейти на незаполненный уровень Ландау. Это связано с существенным изменением энергии.
Если температура Т достаточно низкая, то вероятность такого перехода мала — она пропорциональна  , где
, где  — расстояние по энергии между уровнями Ландау, k — постоянная Больцмана.
— расстояние по энергии между уровнями Ландау, k — постоянная Больцмана.
|
|
|
Таким образом, при T = 0 и при целом факторе заполнения ν продольное сопротивление обращается в нуль. Это означает, что ток течет только вдоль линий постоянного потенциала — эквипотенциалей. При этих условиях выполняет следующее соотношение между концентрацией и магнитным полем 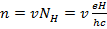 . Тогда холловское сопротивление в двумерном электронном газе будет выглядеть следующим образом:
. Тогда холловское сопротивление в двумерном электронном газе будет выглядеть следующим образом: 
Таким образом, мы получили, что, когда при целых факторах заполнения продольное сопротивление обращается в нуль, а  определяется лишь отношением фундаментальных физических постоянных и целым числом (собственно фактором заполнения).
определяется лишь отношением фундаментальных физических постоянных и целым числом (собственно фактором заполнения).
|
|
|


