Смешанные стратегии: определение, геометрическая интерпретация.

Свойства седловых точек действительной функции двух векторных аргументов.

1) Свойство равнозначности: если a_i1j1 и a_i2j2 (i₁,i₂ , j₁,j₂ ) – седловые точки, то a_i1j1 = a_i2j2

2) Свойство взаимозаменяемости: если a_i1j1 и a_i2j2 (i₁,i₂ , j₁,j₂ ) – седловые точки, то a_i1j2 и a_i2j1 – также седловые точки.

Критерий пессимизма-оптимизма Гурвица оптимальности чистых стратегий относительно выигрышей.

Критерий пессимизма-оптимизма Гурвица относительно выигрышей с показателями оптимизма lÎ[0,1] – взвешенное среднее минимального и максимального выигрышей игрока А при выбранной им стратегии А_i с весами 1 − l и l.

Данный критерий является как бы промежуточным между критериями крайнего пессимизма и крайнего оптимизма и представляет собой частный случай обобщенного критерия Гурвица относительно выигрышей.

Показателем эффективности стратегии A_i по рассматриваемому критерию является величина:

Оптимальной же стратегией по этому критерию считается стратегия A_i0 с максимальным показателем эффективности

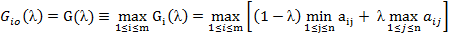
Вообще показатели пессимизма и оптимизма в этом критерии равны соответственно λ_p =1- λ и λ₀ = λ. При λ=0 мы получаем критерий Вальда, а при λ=1 – максимаксный критерий. Чем ближе к нулю показатель оптимизма λ, тем ближе к единице показатель пессимизма 1- λ, и тем меньше оптимизма и больше пессимизма. И наоборот, чем ближе λ к единице, тем больше оптимизма и меньше пессимизма.

Задача теории игр в экономике.

Во многих задачах финансово-экономической сферы возникает необходимость принятия решения. Проблема принятия решения осложняется тем, что ее приходится решать в условиях неопределенности.

В условиях полной определенности теоретические и практические выводы носят однозначный характер и, таким образом, представляют четкое описание ситуации в рамках рассматриваемой задачи. В условиях же недостаточной информированности или полной неопределенности результаты анализа уже не обладают такой четкостью и однозначностью.

Попытка количественного анализа финансово-экономических ситуаций и принятия на их основе решения привела к созданию специальных экономико-математических методов обоснования выбора решений в условиях рыночной неопределенности. Эти методы позволяют находить количественные характеристики экономических процессов, что влечет за собой возможность наиболее полного сравнения исследуемых явлений.

При выборе решения в условиях неопределенности всегда присутствует фактор действия наудачу без обоснованной уверенности в успехе. Он неизбежно присутствует в различных хозяйственных операциях (коммерческий риск), в выполнении предприятием определенного заказа (производственный риск), в выполнении фирмой финансовых обязательств перед инвестором (кредитный риск), в решении купить акции или другие ценные бумаги (инвестиционный риск), в решениях положить деньги в банк (финансовый риск). Математические методы обоснования решений дают возможность анализа вариантов решения с целью уменьшения риска, которое иногда достигается за счет получения дополнительной информации. Математизация содержательных финансово-экономических задач о принятии решениях в условиях неопределенности приводит к соответствующим экономико-математическим моделям и методам, теоретический аспект которых составляет теорию игр. Таким образом, задачами теории игр в экономике являются задачи о выборе решений в условиях экономической неопределенности.

Смешанные стратегии: определение, геометрическая интерпретация.

Смешанная стратегия игрока - стратегия игрока, состоящая в случайном выборе им 1 из своих чистых стратегий с определенной вероятностью;

Смешанная стратегия – линейная комбинация чистых стратегий с коэффициентами, равными вероятностям чистых стратегий, поэтому смешанную стратегию, например, игрока А, имеющего m чистых стратегий, можно представить m -мерным вектором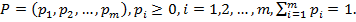

Правая часть равенства является выпуклой комбинацией орт А₁,...,А _m и потому мн-во S_A всех смешанных стратегий геометрически представляет собой фундаментальный (m -1)-мерный симплекс с m вершинами в точках А₁,...,А _m, пред­ставляющих чистые стратегии (выпуклая оболочка, натянутая на чистые стратегии).

Например, при m = 1 игрок А обладает одной чистой страте­гией A₁ и потому смешанная стратегия совпадает с чистой. Таким образом, мн-во смешанных стратегий состоит из единст­венного элемента А₁: S_A= 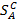={А₁} - и представляет собой 0-мерный симплекс, состоящий из единственной точки - верши­ны А₁. (Рис. 1)

При m = 2 игрок А имеет 2 чистые стратегии: 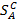={А₁, А₂}, а мн-во S_A смешанных стратегий есть 1-мерный симплекс с двумя вершинами А₁ и А₂, представляющий собой отрезок с концами А₁, и А₂. (Рис. 2)

При m = 3 у игрока А 3 чистые стратегии: 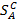={А₁, А₂, А₃}; мн-во S_A смешанных стратегий является 2-мерным симплек­сом с вершинами А₁, А₂, А₃, представляющим собой плоский правильный треугольник А₁ А₂ А₃. (Рис. 3)

p₂

При m = 4 множество смешанных стратегий S_A есть 3-мерный симплекс с четырьмя вершинами А₁ А₂, А₃, А₄, представляю­щий собой правильный тетраэдр. (Рис. 4)

Аналогичная геометрическая интерпретация имеет место и для игрока В, мн-во чистых стратегий которого ={B₁, …, B_n}представляет собой множество п вершин B₁, …, B _n (n -1)-мерного симплекса смешанных стратегий.

1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: