 |
Смешанные стратегии. Геометрическая интерпретация множества смешанных стратегий. (20 баллов).
|
|
|
|
Смешанная стратегия, это чередуемые случайным образом чистые стратегии, с определенными вероятностями (частотами).
Множество SA смешанных стратегий геометрически представляет собой (m-1)-мерный симплекс c m вершинами А1…Аm представляющих собой чистые стратегии
m=1
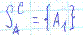
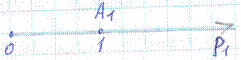
m=2
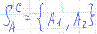
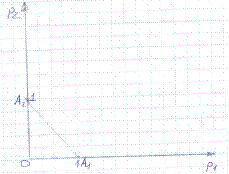
m=3
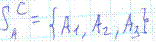
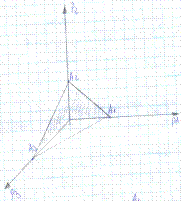
m=4
28.Теорема о сведении решения матричной игры к решению пары двойственных друг другу стандартных задач линейного программирования.
Решение матричной игры m 
n с матрицей игры A эквивалентно решению пары двойственных друг другу стандартных задач линейного программирования:
1. н-ти min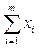 
при огран-иях xi≥0, i=1,…,m, 
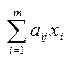≥1, j=1,…,n;
2. н-ти max 
при огран-иях yj≥0, j=1,…,n; 
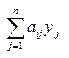≤1, i=1,…,m,
где элементы матрицы A aij>0, i=1,…,m, j=1,…,n. (3)
Точнее говоря, если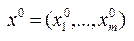 
- оптимальное решения задачи 1, а 
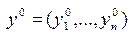- оптимальное решение задачи 2, то
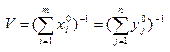(4) - цена игры с матрицей A,
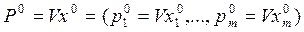(5) - оптимальная стратегия игрока А,
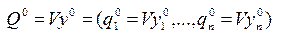(6) - оптимальная стратегия игрока B.
Верно и обратное утверждение. Если P0 и Q0 – оптимальные стратегии соответственно игроков А и B,а V – цена игры, то
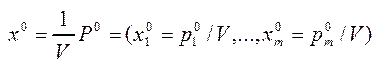(7) - оптимальное решение задачи 1, а 
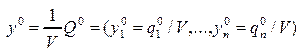(8) - оптимальное решение задачи 2.
Доказательство. Во-первых, необходимо доказать, что задачи 1 и 2 имеют хотя бы по одному допустимому решению.
На основании неравенств 3 можно утверждать, что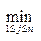 
aij>0, i=1,…,m. Учитывая это, обозначим через 
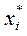, i=1,…,m, произвольные числа, удовлетворяющие неравенствам 
, i=1,…,m. (9)
Из этих неравенств в силу неравенства 3 получим 
, i=1,…,m, j=1,…,n, и потому 
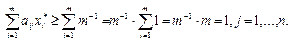
Таким образом, вектор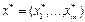 
, удовлетворяющий условию 9, положителен и удовлетворяет ограничениям задачи 1, т. е. является допустимым решение этой задачи.
Допустимым решением задачи 2 является нулевой вектор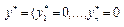 
, поскольку он неотрицателен и удовлетворяет ограничениям задачи 2.
|
|
|
В задаче 1 целевая функция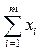 
на допустимом множестве ограничена снизу 
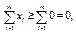а в задаче 2 
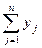на допустимом множестве ограничена сверху, поскольку 
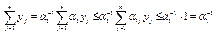, где 
.
Таким образом, из непустоты допустимых множеств решений и ограничения с соответствующей стороны целевых функций следует существование для каждой задачи хотя бы одного оптимального решения.
Пусть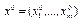 
и 
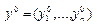- оптимальны решения соответственно задач 1 и 2.
Решение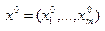 
неотрицательно и не может быть нулевым, поскольку это противоречило бы ограничениям задачи 1. Поэтому хотя бы одна из координат вектора 
положительна и, следовательно,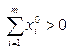 
. В таком случае согласно критерию оптимальности решений взаимно двойственных задач линейного программирования 
.
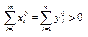Учитывая это неравенство, а также 4, 5 и 6, получим
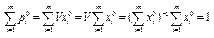, i=1,…,m, 
,
, о=1,…,m,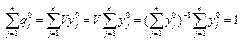 
,
т.е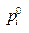 
, i=1,…,m, и 
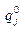, j=1,…,n, являются вероятностями 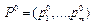и 
и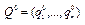 
- смешанные стратегии соответственно игроков А и В. Теперь покажем, что эти смешанные стратегии являются оптимальными. Используя определения 
и 
и 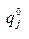ограничения 1 и 2, получим следующие неравенства 
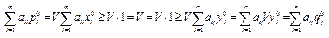, которые, используя формулы 
, (10)
где координаты чистой стратегии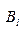 
игрока В представлены с помощью символа Кронекера в виде 
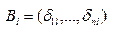, l=1,…,n; 
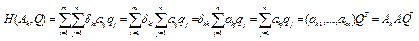, (11)
где координаты чистой стратегии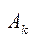 
игрока А представлены в виде 
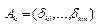, k=1,…,m, можно переписать в виде
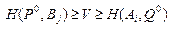, i=1,…,m, j=1,…,n. (11)
Это двойное неравенство является критерием того, что V будет ценой игры, а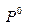 
и 
- оптимальными стратегиями игроков.
Теперь докажем обратную часть теоремы. Пусть V - цена игры, а 
и 
- оптимальные стратегии игроков. Тогда верно следующее неравенство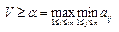 
, откуда в силу 3 получаем V>0. В этом случае можно определить векторы 
и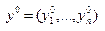 
по формулам 7 и 8 и получить
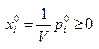, i=1,…,m, (12)
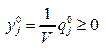, j=1,…,n. (13)
По формулам 10 и 7 и неравенству 11 получим
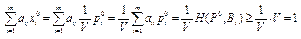, (14)
где j=1,…,n,
по формулам 10, 8 и 11 получим
, (15)
где i=1,…,m.
Неравенства 12 и 14 означают, что вектор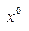 
, определяемый 7, является допустимым решением задачи 1, аналогично 13 и 15 для 
. При этом значения целевых функций из 1 и 2 на соответствующих допустимых векторах 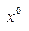и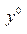 
равны 1/V. Следовательно, по достаточной части критерия оптимальности допустимых решений взаимно двойственных задач линейного программирования решения 
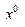и 
являются оптимальными.
|
|
|
Теорема доказана.
|
|
|
