 |
Критерий Лапласа оптимальности чистых стратегий относительно выигрышей.
|
|
|
|
Критерий Лапласа оптимальности относительно выигрышей – Критерий Байеса относительно выигрышей с равновероятными состояниями природы, по которому оптимальной считается стратегия Aio с максимальным показателем эффективности по этому критерию, то есть 
, где 
– взвешенно среднее выигрышей aij игрока А при выборе им стратегии Ai и при состоянии природы Пj с весовыми коэффициентами qj, представляющими собой вероятности состояний природы Пj. При Лапласе ситуация, когда игрок А лишен возможности определить состояния природы, то он вынужден оценивать их субъективно. Один из способов предположить q=1/n, j=1…n, тогда показатель эффективности чистых стратегий по критерию Лапласа относительно выигрышей называется среднее арифметическое io строки матрицы 
. Аio оптимальная, если . Оптимальная среди чистых стратегий по критерию Лапласа является оптимальной по тому же критерию среди смешанных стратегий.
Теорема о соотношении между нижней и верхней ценами игры в смешанных и чистых стратегиях.
Теорема. Нижняя цена игры α и верхняя цена игры β в чистых стратегиях, нижняя цена игры 
и верхняя цена игры 
в смешанных стратегиях удовлетворяют следующим неравенствам: 
Начнем доказательство с неравенства 
. По определению нижней цены игры в смешанных стратегиях 
. Здесь правая часть не зависит от Р и потому это неравенство остается верным и для Р=Аi, i=1…m. Так как полученное равенство будет справедливым в частности для того номера i, который максмизирует показатель эффективности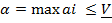 
, Доказано.
Докажем второе неравенство 
. Для любых Р принадлежащих Sa и Q принадлежащих Sb имеем: 
Так как утверждение справедливо для любых Р принадлежащих принадлежащих Sa и Q принадлежащих Sb, то 
|
|
|
Докажем третью часть 
. 
. Это также верн и для чистых стратегий Q=Bj, j=1,…,n игрока В 
. Следовательно, 
ч.т.д.
Функция выигрыша в смешанных стратегиях: запись в координатной и матричной формах.
Определим функцию выигрыша игрока А в смешанных стратегиях как функцию Н, заданную на декартовом произведении SA x SB множеств смешанных стратегий, ставящую в соответствие каждой ситуации (P,Q) 
SA x SB в смешанных стратегиях средний выигрыш игрока А в этой ситуации, определяемый выражением 
. Таким образом,H(P,Q) = , (P,Q) SA x SB, где P=(p1,…..,pm), Q=(q1,….,qn) -координатная форма задания функции выигрыша в смешанных стратегиях.H(P,Q) = PAQT – матричная форма функции выигрыша, где P=(p1,…,pm) – вектор-строка размера 1хm,А= 
– матрица игры(выигрышей игрока А в чистых стратегиях) размера m x n, QT = 
Основные понятия и определения теории игр. Классификация игр.
Теория игр – теоретическая основа математических моделей, принятие оптимальных решений в конфликтной ситуации рыночных отношений.
Неопределенность – действия сторон, направленных на уменьшение эффективности другой стороной. Риск – вероятность неблагоприятного исхода.
Конфиктная ситуация – столкновение интересов, не менее 2х сторон каждая из которых для достижения своей цели имеет возможность действовать различными способами в зависимости от действий противоборствующих сторон.
Характеризуется: а)наличие заинтересованных сторон – игроков, б)существование возможных действий у каждой стороны – стратегий, в) интересами сторон, удовлетворяющих различные эконом, соц, полит потребности. Стратегия: А-игрок А, m>=1-стратегий, => 
, А-игрок А, т>=1-стратегий 
Игра – математическая модель конкретной ситуация. Конфликт первичен.
Коалиции - объединение игроков.(по причинам- действия, интересов, и действ и инт; временный: пост и временные; числу участ: парные и множеств)
|
|
|
Правила игры – система условий с целью формализации (записи на мат. язык некоторых утверждений).а) Стратегии чистые – детерминированные, смешанные – смесь разных стратегий. Б)объем инфы, к-й каждый из игроков может получить о действиях игрока. с) исход игры в результате совокупности стратегий игроков.
В условиях конфликтных ситуаций каждый игрок определяет стратегию, в результате образуется набор ситуаций – исход игры. Исход – набор всех ситуаций. Запрещенные – недопустимые по правилам игры, если так, то игра не состоится.
Функция выигрыша игрока А в чистых стратегиях Fa-степень удовлетворенности интересов игрока А. 
, x э Х, аналогично 
Функция выигрыша игрока В в чистых стратегиях Fв - степень удовлетворенности интересов игрока В
Классификация игр: 1)от воз-сти образования коалиций а)коалиционные – для макс. Коалиционного выигрыша, в) бескоалиционные – индивидуальный выигрыш; 2) по числу множественные – более 2х игроков, парные – 2 игрока. В парных играх игроки преследует противоположные цели – антагонистические (нулевая сумма выигрыша), игры с природой – один из игроков неосознанно –природа. В) мощность множества стратеги – а)конечные игры – если множество стратегий конечные, б) бесконечные – множество большее, чем четное.
|
|
|
