Выигрыш-функции игроков в антагонистической игре: области определения, области значений.

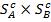Степень удовлетворения интересов игрока А характеризуется функцией выигрыша игрока А , определенной на мн-ве Х= всех ситуаций и ставящей в соответствие каждой ситуации x 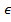X некоторое число F_A (x) 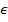R, называемое выигрышем игрока А. (т.е. обл. определения это Х, обл. значения- R- мн-во действ. чисел).

Аналогично, для игрока В функция выигрыша F_B:Y 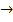R определена на мн-ве Y= 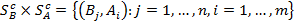ситуаций y=(B_j,A_i) и каждой из них ставит в соответствие число F_B(y) 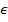R, называемое выигрышем игрока В. (т.е. обл. определения это Y, обл. значения- R-мн-во действ. чисел).

В антагонистической игре выполняется: F_A(x)=-F_B(y).

56.=45

57. Определение выигрыш-функции в смешанных стратегиях: координатные и векторно-матричные формулы ее представления. (26 баллов) (=14)

58. Редуцирование игр, привести пример. (24 балла) (=81)

59. Понятие седловых точек действительной функции двух векторных аргументов. (20 баллов) (=95)

60. Показателем неэффективности стратегии A_i по критерию Байеса относительно рисков является средний риск:

этот показатель является взвешенным средним рисков i-й строки матрицы рисков с весами q_j, j = 1,…, n.

Оптимальной среди чистых стратегий по критерию Байеса относительно рисков является стратегия A_i0, показатель неэффективности которой минимален, то есть минимален средний риск.

В качестве показателя неэффективности смешанной стратегии 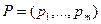по критерию Байеса относительно рисков.

Оптимальной среди всех смешанных (в том числе и чистых) стратегий по критерию Байеса относительно рисков будем считать стратегию Р⁰, показатель неэффективности которой минимален.

61. Теорема. (Критерии оптимальных стратегий).

Пусть V-цена игры, H(P,Q) – выигрыш-функция, S_A и S_B – множества смешанных стратегий соответственно игроков А и В.

1. Для того чтобы стратегия Р^О игрока А была оптимальной, необходимо и достаточно, чтобы выполнялось неравенство:

H(P^О,Q)≥V

Для любого Q ϵ S_B, т.е. выбор игроком А оптимальной стратегии Р^О гарантирует ему выигрыш H(P^О,Q), не меньший цены игры V, при любой стратегии Q игрока В.

2. Для того чтобы стратегия Q^O игрока В была оптимальной, необходимо и достаточно, чтобы выполнялось неравенство

H(P^О,Q)≤V

Для любого Р ϵ S_А , т.е. выбор игроком В оптимальной стратегии Q^О гарантирует ему проигрыш H(P,Q^О), не больший цены игры V, при любой стратегии Р игрока А.

Данная теорема остаётся справедливой, если в её формулировке множество смешанных стратегий S_A и S_B заменить соответственно на множество чистых стратегий S^С_A и S^С_B.

Доказательство:

Утверждение 1:

Необходимость:

Пусть Р⁰ – оптимальная стратегия игрока А. тогда по теореме фон Неймана показатель эффективности стратегии Р⁰ равен цене игры V:

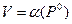(1)

Рассматривая как показатель эффективности стратегии Р⁰ относительно множества S _B смешанных стратегий игрока В, будем иметь по определению:

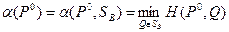(2)

Из равенств (1) и (2) получаем неравенство H(P^О,Q)≥V

Достаточность:

Пусть для некоторой стратегии Р0 игрока А выполняется неравенство H(P^О,Q)≥V. Для доказательство оптимальности стратегии Р0 достаточность показать справедливость равенства

Так как неравенство выполняется для любой стратегии 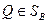игрока В, то

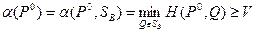(3)

Но цена игры V равна нижней цене игры V, по определению которой

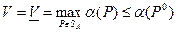(4)

Совокупность (3) и (4) эквивалентна равенству . Достаточность доказана

Утверждение 2:

АНАЛОГИЧНЫЕ РАССЖУДЕНИЯ.

62. Для того, чтобы существовала цена игры в чистых стратегиях, то есть для того, чтобы нижняя цена игры равнялась верхней цене игры необходимо и достаточно, чтобы у матрицы существовала седловая точка.

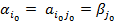Седловая точка, это ситуация, при которой удовлетворяются интересы каждого из игроков А и В, то есть если выполняются неравенства или , где 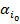- нижняя цена игры(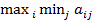), а 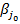- верхняя цена игры(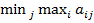). Таким образом элемент 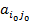является минимальным в 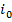-ой строке и максимальным в 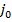-ом столбце. При этом оптимальными чистыми стратегиями для игроков А и В будут стратегии обеспечивающие выигрыш 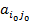игроку А и проигрыш 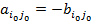игроку В.

63. Пусть имеем 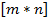– игру с матрицей выигрышей А игрока А. Ситуация (A _k, B _l), сложившаяся в результате выбора игроками А и В соответственно стратегий A _k и B _l, 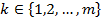, , называется удовлетворительной для игрока А, если

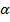_{il 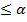kl}, i =1,2,…, m

Ситуация (A _k, B _l) будет удовлетворительной для игрока А тогда, и только тогда, когда его выигрыш 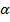_kl совпадает с показателем неэффективности _l стратегии B _l игрока В:

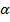_kl = _l

т.е. будет максимальной в l -м столбце матрицы А.

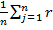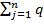64. Критерий Байеса относительно рисков при равновероятных состояниях природы, q₁ =…= q_n =1/n, превращается в критерий Лапласа относительно рисков. Тогда величина _ij, получающаяся из _i = q₁r_i1 + q₂r_i2 + …+q_nr_in = _jr_ij, i=1,…,m при q_j=1/n, j=1,2,…n, или более простая величина 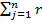_ij представляет собой показатель неэффективности стратегии А_i по критерию Лапласа относительно рисков. Следовательно, оптимальной среди чистых стратегий по критерию Лапласа относительно рисков является стратегия A_{ij ,} показатель неэффективности 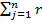_ioj который минимален.

Подставляя в (P) = 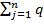_jr(P,П_j) значения q_j=1/n, j=1,…, n, получим показатель неэффективности смешанной стратегии Р по критерию Лапласа относительно рисков, вместо которого можно рассматривать более простую величину (P) = 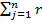(P,П_j). Стратегия Р, для которой показатель 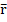(P) принимает минимальное значение, является оптимальной среди всех стратегий множества S_A.

65.=39

⇐ Предыдущая1234567

Поделиться:

Воспользуйтесь поиском по сайту: