Непосредственные дедуктивные умозаключения

В зависимости от числа посылок, из которых можно сделать тот или иной вывод, дедуктивные умозаключения подразделяются на непосредственные и опосредованные.

Непосредственное умозаключение - такое, которое делается из одной посылки.

Опосредованные умозаключения - такие, которые делаются из двух и более посылок.

Как возможно умозаключение через преобразование суждений? Дело в том, что нам уже известно отношение S суждения к Р суждению. И мы выводим новое знание о других отношениях этих элементов суждения - P к S, S к не-P, Р к не-S и не-P к S.

Правило непосредственного умозаключения: термин, не распределенный в посылке, не может быть распределен в заключении. Первым делом при изучении непосредственных умозаключений рассматривают умозаключения путём преобразования суждений - превращение, обращение и противопоставление предикату. Эти операции мы уже изучали в предыдущей лекции, поэтому переходим к следующему виду непосредственных умозаключений.

В "логическом квадрате" имеют место такие важнейшие отношения между суждениями, как 1) логическое подчинение, 2) субконтрарность (частичная совместимость), 3) противоположность (контрарность), 4) противоречие (контрадикторность).

Непосредственные умозаключения возможны в "логическом квадрате", потому что между суждениями, находящимися в этих отношениях существуют определенные зависимости по истинности и ложности. Поскольку каждое суждение - A, E, I, O - может находиться в трех отношениях с другими, из него можно сделать три вывода.

Например: Если истинно А, "Все рецидивисты - преступники", то отсюда следует, что 1) тем более истинно частноутвердительное суждение I: "Некоторые рецидивисты - преступники" (отношение подчинения); 2) что ложно Е: "Ни один рецидивист - не преступник" (отношение противоположности); и 3) что ложно О: "Некоторые рецидивисты - не преступники".Другой пример: Если ложно А, что "Все философы - материалисты" (ведь есть и идеалисты), то какие выводы можно сделать отсюда? Истинно О: "Некоторые философы - не материалисты" (отношение противоречия). Е будет неопределенным - "Ни один философ не материалист", в данном же случае это ложно, (отношение противоположности). I также будет неопределенно - "Некоторые философы - материалисты" (отношение подчинения), но в данном случае мы по своему опыту знаем, что оно истинно.

Таким образом, среди умозаключений по логическому квадрату выделяют следующие подвиды:

Умозаключение противоречия, которое основывается на логическом законе исключенного третьего, согласно которому если утверждение чего-либо истинно, то отрицание ложно и наоборот.Умозаключение противоречия позволяет установить отношения между суждениями типа А и О, Е и I, это и есть противоречащие суждения.Предположим, необходимо установить истинность Е. Это возможно сделать, если нам удастся установить ложность I. Если же нам необходимо установить истинность О, то при невозможности сделать именно это - надо установить ложность А.Умозаключение противоположности происходит на базе закона противоречия. Заключением такого умозаключения является ложное суждение. В подобных заключениях вывод делается либо о ложности общего суждения, либо о ложности единичного суждения. Истинного заключения здесь не сделать, ибо, как мы знаем, противоположные суждения могут быть одновременно ложными. Например: Из истинного суждения "Ни один человек не рыба" устанавливается ложность суждения "Все люди - рыбы".

Умозаключение субконтрарности дает возможность получить истинные частноутвердительные или частноотрицательные суждения. Например: Из истинного суждения: "Некоторые философы были материалистами" можно получить истинное суждение в виде заключения - "Некоторые философы не были материалистами". Однако здесь более значимым является знание о том, что одно из таких суждений (I или О) является ложным. Тогда с необходимостью следует, что другое – истинно, ибо одновременно ложными они быть не могут.

Умозаключение подчинения позволяет получать истинные частноутвердительные или частноотрицательные суждения. Вместе с тем умозаключения подчинения дают возможность сделать вывод о ложности общеутвердительных или общеотрицательных суждений. Например: Если ложно I "Некоторые люди являются растениями", то ложно и А "Все люди являются растениями".

Непосредственные умозаключения могут быть получены (не только из атрибутивных суждений) также из простых суждений с отношениями реляционных суждений. Логическим основанием здесь служит характер отношения R между предметами X и Y. Например: Если известно, что "Женщины равны в правах с мужчинами", то можно заключить, что "Мужчины равны в правах с женщинами". Если известно, что "Конституционные законы выше всех остальных законов страны", то следует отсюда, что "Остальные законы не выше (ниже) конституционных".

Контрапозиция простая - условное умозаключение, логическая форма которого такова:

.

Если завтра будет солнечно, то мы пойдем копать картошку.

Если мы не пошли копать картошку, то был дождь.

Контрапозиция сложная - .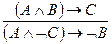

Если завтра будет солнечно и у нас будут силы, то мы пойдем валить лес.

Если сегодня солнечно и мы не валим лес, то у нас нет сил.

Импотация - .

Экспортация - .

Есть также 4 умозаключения модальности, под которыми имеют в виду отношения между суждениями, характеризуемыми некоторыми логическими модальностями. Например, если неверно, что 6 × 3 = 23, то нет такого положения дел в котором 6 × 3 = 23.

Подытоживая сказанное, подчеркнем, что благодаря непосредственным умозаключениям из уже известного знания извлекается дополнительная и самая разнообразная информация.

Главное, чтобы в каждом отдельном случае соблюдались специфические правила или принципы таких умозаключений, чтобы избежать ошибок в рассуждении.