 |
4 Дәріс. Қозғалтқыштардың теориясы. Жұмыс барысының теориясы және энергетикалық қондырғылардың есебі
|
|
|
|
4 Дә ріс. Қ озғ алтқ ыштардың теориясы. Жұ мыс барысының теориясы жә не энергетикалық қ ондырғ ылардың есебі
4. 1 Іштен жанатын піспекті қ озғ алтқ ыштың термодинамикалық барыстары
Термодинамика ғ ылымы – жылу энергиясының механикалық энергияғ а айналу қ ұ былысын зерттейтін ғ ылым. Іштен жанатын піспекті қ озғ алтқ ыштарда жү ретін қ ұ былыстардың барлығ ы да осы термодинамикалық қ ұ былыстар заң ына бағ ынады. Бірақ термодинамикалық қ ұ былыстар идеалдық газдардың идеалдық таза барыстарына негізделген, ал іштен жанатын піспекті қ озғ алтқ ыштардағ ы барыстар табиғ и нағ ыз газдардың аралас қ ұ былыстары арқ ылы жү ретін барыстар.
Жылу энергиясын механикалық энергияғ а алмастыру кезіндегі негізгі жұ мысшы мү ше, ол ә ртү рлі газдар болып табылады. Олардың басқ а заттардан ерекшелігіне бос кең істікті тез толтырып, қ ысымғ а байланысты кө лемін жә не температурасын ө згерте алатындығ ын жатқ ызуғ а болады. Сондық танда газдар сырттан жылуды тез қ абылдап немесе сыртқ а жылуды тез бере алады, яғ ни осындай жылу алмасуының салдарынан механикалық жұ мыс пайда болады.
Осындай қ олданылатын идеалдық газдардың жағ дайы газ кү йінің теориялық тең деуімен ө рнектеледі, яғ ни:
pV = GRT, (8)
мү ндағ ы: p – газ қ ысымы, H/м2; V – газ кө лемі, м3; Τ – газдың абсолюттік температурасы, °К; G – газ массасы, кг; R – газ тұ рақ тысы, Дж/(кг·град. ). Бұ л газ қ асиетіне байланысты, мысалы ауа ү шін R=287 Дж/(кг·град. ). Осы келтірілген газ кү йінің тең деуіне жү гінсек, мынандай қ ортынды жасауғ а болады: белгілі бір мө лшердегі газдың кез-келген бір кө рсеткіші ө згерсе, онда оның басқ а кө рсеткіштері де міндетті тү рде ө згереді. Мысалы кез келген бір газды қ ыздырып температурасын кө терсек, оның міндетті тү рде кө лемі немесе қ ысымы ө згереді. Іштен жанатын қ озғ алтқ ыштардың жұ мыс барысы газдардың осы қ асиетіне негізделген.
|
|
|
Идеалды газдардағ ы осы ө згерістер тө рт тү рлі жағ дайда (6 сурет) ө туі мү мкін:
Егер газ кө лемі тұ рақ ты болса, яғ ни V=const, онда ондай барысты изохоралық барыс деп атаймыз. Бұ л кезде газ қ ысымының ө згерісі ордината осіне параллель болады, ал басқ а екі кө рсеткіштері (р, Т) бір-біріне пропорционал ө згереді, яғ ни
(р2/р1) = (Т2/Т1), (9)
мұ ндағ ы р1 мен T1 – барыс алдындағ ы, ал р2 мен Т2 барыс соң ындағ ы газ кысымы мен температурасы.
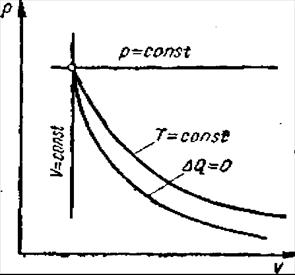
Сурет 6 – Теориялық термодинамикалық барыстар
Газ кысымы тұ рақ ты кездегі, яғ ни p = const кезіндегі барысты изобаралық барыс деп атайды. Бұ л кезде газ кө лемі мен температурасы бір біріне пропорционал ө згереді (Гей-Люссак заң ы), яғ ни
(V2/V1) = (T2/T1). (10)
Мұ нда да барыстың алды мен соң ғ ы кү йіндегі газ кө рсеткіштері берілген.
Меншікті қ ысым мен тығ ыздық тың арасында мынадай тә уелділік бар
ρ ν =1 или ρ =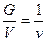 
, (11)
|
|
|
мұ ндағ ы ρ – бір кубтық метр газдың салмағ ы, кг/м3.
(10) тең деуге ν орнына ρ қ оятын болсақ
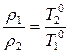. (12)
Τ =const кезіндегі барысты изотермиялық барыс деп атайды, ал бұ л кездегі газ кө лемі (V) мен қ ысымы (р) бір біріне кері пропорционал ө згереді (Бойль-Мариотта заң ы), яғ ни
(V2/V1) = (p1/p2). (13)
Егер барыс сыртпен жылу алмаспай жү ретін болса, яғ ни Δ Q=0 болса, онда мұ ндай барысты адиабаттық барыс деп атайды. Бұ л кездегі газ кү йінің ө згерісі адиабаттық барыстың кө рсеткішіне тә уелді ө згереді, яғ ни
(V2 / V1)k = (р1 / р2), (14)
немесе
(V2/V1)k-1 =T2/T1), (15)
мұ ндағ ы k - адиабаттық барыстың кө рсеткіші. Ол тү рлі газдар ү шін ә ртү рлі болады, ал ауа ү шін k = 1, 41 егер Τ = 288°К болса. Себебі температура кө терілген сайын бұ л кө рсеткіш аздап тө мендейді.
Жоғ арыда қ аралғ ан теориялық термодинамикалық барыстар нағ ыз осы айтылғ ан тү рлерінде табиғ атта кездеспейді. Олардың тек ө згеше аралас тү рлері болады. Ондай барысты политроптық барыс деп атайды, яғ ни бұ л аталган барысы жү ргенде жоғ арыда келтірілген жағ дайлар сақ талмайды. Мысалы кө лем, қ ысым, температура тұ рақ ты болмайды, ал сыртпен міндетті тү рде жылу алмасуы болады.
Политроптық барыс адиабаттық барысқ а ұ қ сас жү реді, ал оның кө рсеткіші адиабаттық кө рсеткіштен ө згеше болады. Политроптық барыстың жү ру заң дылығ ы мына адиабаттық барыстың жү ру заң дылығ ына ұ қ сас формуламен ө рнектеледі, яғ ни
( V2 / V1 )n = (р1 / p2), (16)
|
|
|
немесе
(V2/V1)n+1 = (T2/T1), (17)
мұ ндағ ы n - политроптық барыстың кө рсеткіші.
Термодинамикалық заң дылық тарғ а сү йене отырып, қ ысу кезіндегі политроптық барыстың кө рсеткіші n адиабаттык барыстың кө рсеткішінен аз болып, бірақ бірден артық болса, яғ ни k> n> 1, 0 онда жылу сыртка шығ арылады, ал n> k болса, онда барысқ а сырттан жылу беріледі. Ұ лғ аю барысы кезінде осығ ан керісінше болады, яғ ни k > n> 1, 0 болғ анда газғ а сырттан жылу беріледі де n> k болғ анда сыртка жылу шыгарады.
Клайперон-Менделеев тең деуі: «Газдың қ ысымы мен температурасы ө згерген кезде оның меншікті кө лемі температурағ а тура пропорцинал жә не қ ысымғ а кері пропорционал ө згереді», яғ ни
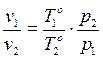(18)
немесе
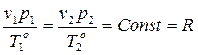, (19)
мұ ндағ ы R – газ тұ рақ тысы, Дж/(моль·град).
Авогадро заң ы: «Температурасы мен қ ысымы бірдей болғ ан кезде тең кө лемдер ә ртү рлі газдардың бірдей мө лшердегі молекулаларын сидырады». Сондық тан екі газдың молекулярлық салмақ тары m1 жә не m2 олардың тығ ыздық тарына ρ 1 жә не ρ 2 тура пропорционал жә не меншікті кө лемдеріне ν 1 жә не ν 2 кері пропорционал, яғ ни
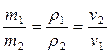, (20)
осыдан
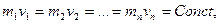(21)
яғ ни барлық газдардың 1 молінің кө лемдері бірдей температура мен бірдей қ ысымда бірдей болады. Килограмм-моль – сан мө лшермен алғ андағ ы заттың молекулярлық салмағ ына тең килограмм саны.
|
|
|
Газдың меншікті кө лемінің молекулярлық салмағ ына кө бейтіндісі (mν ) моль кө лемі деп аталады.
Мысалы, оттегінің бір молінің кө лемі (m=32 кг/моль), кө лемдік массасы ρ =1, 31 кг/м3 болғ ан кезінде (қ ысымы 0, 1 МПа жә не температурасы 150С кезінде) тө мендегідей болады
Vмоль=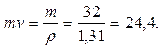 
Барлық газдардың бір молінің кө лемі тұ рақ ты мө лшерде 24, 4 м3/моль тең болады.
Газдың бір молінің салмағ ы Gмоль молекулярлық салмағ ына тең болады
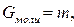кг/моль.
Газдың моль саны М оның ауырлығ ының G молекулярлық салмағ ы m қ атынасына тең болады, яғ ни
М =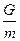 
. (22)
Газдың меншікті кө лемі ν бір мольдің кө лемі Vмоль бө лінген оның салмағ ына m тең болады, яғ ни
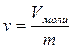, м3/кг. (23)
Іштен жанатын піспекті қ озғ алтқ ышдтардағ ы жү ретін нағ ыз барыстар жоғ арыдағ ы барыстардан ө згеше болады. Сондық танда бұ л барыстардың циклын ү ш тү рге бө луге болады: теориялық яғ ни цикл идеалдық барыстардан тұ рады; есептік барыстар, яғ ни қ ысу мен ұ лғ аю барыстары политроптық барыс болады; нақ ты цикл, яғ ни бұ л қ озғ алтқ ыш цилиндрінің ішінде жү ретін барыстардың индикаторлық циклы.
|
|
|
