Алгоритмы и модели информационного поиска

Классические модели информационного поиска рассматривают документы как множества представляющих эти документы ключевых слов, в дальнейшем называемых термами (словоформами). Терм – это обычно слово, семантика которого помогает описать основное содержание документа.

Формально описание любой модели информационного поиска состоит из четырех частей [17; 33]:

- D – множества используемых типов представлений документов;

- Q – множества используемых типов описаний информационных потребностей пользователя, т. е. запросов [4; 13];

- F – общего каркаса, в рамках которого происходит моделирование описаний документов и запросов, а также описание взаимосвязей между ними;

- R (q, d_i) – функции ранжирования, которая паре «I -й документ(d_i) – запрос(q)» сопоставляет некоторое вещественное число.

Модели информационного поиска делятся на три класса:

- теоретико-множественные модели, использующие теорию множеств. Классический пример модели этого класса – булева модель, в рамках которой документы и запросы представляются в виде множеств термов;

- вероятностные модели. Каркасом таких моделей выступает теория вероятностей, а в качестве оценки релевантности документа запросу пользователя берется вероятность того, что пользователь признает документ истинно релевантным;

- алгебраические модели. В рамках этих моделей документы и запросы описываются в виде векторов в многомерном пространстве. В основе таких моделей лежат алгебраические методы [97].

Следует отметить, что наиболее популярными являются алгебраические модели, поскольку их практическая эффективность обычно оказывается выше других моделей. Предлагаемые в последнее время новые модели информационного поиска зачастую являются гибридными и обладают свойствами моделей разных классов [97].

Необходимо отметить, что практически все алгоритмы поиска информации в Интернете используют теорию графов. И это не случайно, так как Сеть можно представить как граф огромных размеров, где страницы являются узлами, а ссылки на другие страницы – дугами. При этом для каждой страницы ссылка, выходящая из нее (исходящая дуга), называется Forward, или Outcoming Link (Outedge, Outcoming Arc), а ссылка, указывающая на эту страницу (входящая дуга), – Backlink (Inedge). Обозначим факт наличия ссылки со страницы u на страницу v следующим образом: 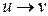. Заметим, что все исходящие ссылки можно легко извлечь из страницы и почти всегда их количество не очень велико, так как оно определяется только хозяином страницы, тогда как для нахождения входящих дуг необходима информация о структуре интернет-сайта, а их количество может оказаться очень большим, хотя обычно оно невелико. Наличие ссылки со страницы u на страницу v в общем случае трактуется как факт оказания предпочтения странице v автором страницы u. Конечно, не все ссылки соответствуют данному утверждению, например навигационные, которые созданы для удобства перемещения по разным страницам сайта. Практически всегда результатом работы алгоритма ранжирования является присвоение каждой странице из рассматриваемого набора некоторого веса, обычно неотрицательного вещественного, и последующее упорядочивание набора страниц. Проранжированная таким образом информация предоставляется ЛПР.

Рассмотрим алгоритмы и модели, используемые на всех этапах поиска многоязычной информации.

Алгоритм PageRing

Существуют алгоритмы, которые вычисляют веса сразу для всех страниц, проиндексированных поисковой системой. Для этого им необходимо иметь доступ ко всей базе данных поисковой системы, где хранится структура ссылок. Простейшей эвристикой такого рода был подсчет количества входящих ссылок (In-degree). Несколько лет назад таким образом поступали многие поисковые системы [95]. Однако эта модель слишком примитивна, поскольку она не учитывает свойства тех страниц, с которых идут ссылки, тогда как ссылки со специализированных сайтов нередко важнее ссылок с домашних страниц пользователей Интернета. Поэтому в 1998 г. С. Брин и Л. Пейдж разработали алгоритм PageRank [95], основанный на идее распространения ранга по ссылкам со страницу.

Авторы этого алгоритма предлагают модель блуждающего пользователя (Random Surfer Model), который, находясь на странице, случайным образом выбирает на ней ссылку и идет по ней или же оказывается на любой странице в зависимости от некоторого заранее заданного распределения, при этом частота посещения страницы пользователем пропорциональна рангу. Ранг страницы А вычисляется по следующей рекурсивной формуле:

PR (A) = (1 – d) + d (PR (T 1)/ C (T 1) +... + PR (Tn)/ C (Tn)), (3.1)

где PR (A) – это вес PageRank страницы A (тот вес, который нужно вычислить); D – коэффициент затухания, который обычно устанавливают равным 0,85; PR (T 1) – вес PageRank страницы, указывающей на страницу A; C (T 1) – число ссылок с этой страницы; PR (Tn)/ C (Tn) означает, что это делается для каждой страницы, указывающей на страницу A.

Однако у алгоритма PageRank есть серьезный недостаток – проведение поиска информации крайне затруднено необходимостью иметь граф, построенный на основе всего пространства Интернета или, по крайней мере, значительной его части. Даже такая крупная поисковая система, как Goggle, при реализации данного алгоритма не в состоянии охватить весь Интернет, в связи с чем ее весовые коэффициенты не учитывают все входящие ссылки. Кроме того, часть информации, относящаяся к определению ранга страницы по ее весу, вычисленному по алгоритму PageRank, является конфиденциальной и ее можно получить только экспериментально [88; 101].