Алгоритм Клейнберга и его модификации

 

Алгоритм PageRank был доработан Дж. Клейнбергом, который предложил ранжировать не все страницы сразу, а только относящиеся к конкретному запросу [92]. Алгоритм Клейнберга работает по следующей схеме:

– обычной поисковой системе посылается запрос и из ответа извлекается k первых результатов (у Клейнберга k = 200). Полученный таким образом набор ссылок (страниц), отвечающих заданному поиску, называется RootSet;

– к страницам из RootSet добавляются их ближайшие соседи, т. е. те страницы, на которые ссылаются страницы из RootSet, и страницы, которые сами имеют ссылки на страницы RootSet. Для поиска последних также используется поисковая система, причем берется не более d входящих ссылок на одну страницу (в алгоритме Клейнберга d = 50). Так строится BaseSet – набор ссылок с выходом на одну страницу, отвечающий определенному поиску (рис. 3.1);

– далее используется только BaseSet, точнее граф, который он естественным образом порождает, а не весь Интернет. При этом из графа выбрасываются все внутридоменные ссылки, т. е. те ссылки, которые соединяют страницы в пределах одного сайта. Это простейшая эвристика для подавления навигацонных ссылок.

 

 

Рис. 3.1. Построение набора ссылок BaseSet

 

Еще более важная идея алгоритма Клейнберга состоит в том, что веб-страницы разделяются им на две группы: страницы как посредники, или набор ссылок, и страницы как первоисточники собственно информации, и для каждой страницы рассчитываются не один, а два ранга. Такой подход обусловлен наличием в Интернете большого числа сообществ, т. е. наборов страниц близкой тематики, которые весьма сильно связаны друг с другом ссылками (рис. 3.2).

 

 

Рис. 3.2. Пример сообщества (слева – посредники,

справа – первоисточники)

Ранг страницы-посредника тем выше, чем выше ранги страниц-пер-воисточников, на которые она ссылается, а ранг страницы-первоисточника аналогичным образом зависит от посреднических рангов страниц, ссылаю-щихся на нее.

Благодаря возможности проводить эксперименты без больших затрат вычислительных ресурсов многие исследователи независимо друг от друга предпринимали попытки дальнейшего развивития идей Клейнберга. Рассмотрим наиболее успешные из этих попыток.

Система CLEVER. Усовершенствованием своего алгоритма занимался сам Дж. Клейнберг совместно с группой исследователей [32; 95]. Разработанная ими система CLEVER отличается от исходного алгоритма тем, что каждая дуга в графе, порожденном набором ссылок BaseSet, имеет некоторый положительный вес, который затем используется при расчете рангов. Для определения веса ссылки были использованы следующие эвристики:

- вес ссылки повышается, если текст, окружающий определение этой ссылки (Anchor Text), содержит термы запроса, например слова из запроса в заголовке страницы;

- внутридоменные ссылки не удаляются, как в алгоритме Клейнберга, им просто присваиваются малые веса.

Кроме того, когда в одном домене наблюдается несколько страниц с высокими весами, их веса следует уменьшить, чтобы предотвратить доминирование одного сайта.

Еще одна идея, позднее разработанная одним из участников проекта CLEVER, состоит в том, чтобы разбивать большие подборки ссылок, которые посвящены различным темам, на части (pagelet), ранг для каждой из которых рассчитывается отдельно.

Эвристики Бхарата–Хенцингера. Дж. Клейнбергом был описан еще один модифицированный алгоритм – алгоритм сортировки страниц HITS (Hyperlink Indused Topic Distillation). И почти сразу после появления этого алгоритма К. Бхарат и М. Хенцингер выявили несколько причин его неудовлетворительной работы [96].

Во-первых, часто возникает ситуация, когда много страниц одного сайта ссылаются на один документ на другом сайте, например на своего спонсора. Возможна и другая ситуация, когда на одной странице встречается множество ссылок на разные страницы другого сайта. Однако такая конструкция обычно противоречит идее о том, что ссылка выражает предпочтения автора, так как вес такого предпочтения увеличивается в n раз.

Во-вторых, алгоритм HITS рассчитан на использование ссылок, созданных человеком, а не машиной.

В-третьих, отмечается появление в BaseSet совсем не релевантных запросу документов и, как следствие, неоправданное расширение области поиска. Но это свойство алгоритма было описано и самим Клейнбергом.

Для разрешения этих проблем были предложены следующие способы:

- если n страниц одного сайта ссылаются на документ u на другом сайте, то каждой из ссылок, которая участвует в этом, присваивается вес, равный 1/ n. Этот вес используется при вычислении ранга первоисточника страницы u. Аналогичная схема применяется в случае, когда со страницы u есть много ссылок на разные страницы другого сайта;

- еще один способ – удалять из BaseSet те страницы, которые не релеванты запросу. Для определения степени релевантности используется векторная модель. После того как все страницы были сравнены с запросом, выбирается некоторый порог, и все узлы, степень схожести с запросом у которых меньше этого порога, удаляются. В [96] предложено три разных порога: усреднение по всему BaseSet, усреднение по RootSet и одна десятая максимальной степени схожести;

- третий способ – использование схожести с запросом оставшихся страниц в качестве коэффициента при расчете рангов.

Алгоритм PHITS. Существуют и более принципиальные модификации алгоритма HITS. Исследователи Д. Кон и Х. Чанг предложили вероятностный подход и назвали его Probabilistic HITS (PHITS) [87]. PHITS имеет ясную вероятностную модель и построен на более адекватных реальности предположениях о распределении количества входящих ссылок. В этом алгоритме введены следующие обозначения: D – множество цитирующих документов; C – множество цитируемых документов (такое обозначение не значит, что эти два множества не пересекаются, более того, обычно C = D, хотя необходимо подчеркнуть, что их роли различны); Z – множество сообществ (или классов, категорий), к которым алгоритм попытается с некоторой вероятностью отнести каждую страницу. Д. Кон и Х. Чанг рассматривали порождающую модель, где множество генерируется с вероятностью P (d), сообщество x ассоциируется с этим множеством и вероятностью P (z | d), а множество генерируется с вероятностью P (c | x). Оценить построенную модель должна функция правдоподобия:

 

(3.2)

 

где – функция правдоподобия для отдельно взятой ссылки; M – матрица цитирования, т. е. матрица смежности в терминах теории графов, построенная по BaseSet. Задача состоит в том, чтобы подобрать такие P (x), P (c | x) и 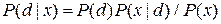, чтобы функция L (M) стала максимальной. Для этого используется итерационный алгоритм Expectation-Maximization, гарантирующий монотонное возрастание L (M). Найденные таким образом P (c | x) соответствуют рангам первоисточников, а P (d | x)– рангам посредников.

Алгоритм SALSA. Еще один вероятностный подход – SALSA – был предложен Р. Лемпелем и С. Мораном. Они разработали новую модель, лежащую в основе алгоритма Клейнберга, но в то же время являющуюся обобщением алгоритма обычного HITS. Р. Лемпель и С. Моран, подобно С. Брину и Л. Пейджу, тоже применили модель блуждающего пользователя, но сделали это несколько иначе, используя теорию марковских цепей. В алгоритме SALSA в BaseSet рассматриваются две цепи Маркова: одна – для обхода подборок ссылок, другая – для обхода первоисточников. Переход из одного состояния цепи в другое эквивалентен переходу не по одной ссылке (как в алгоритме PageRank), а по двум – прямой и обратной (и наоборот). Такая схема работает только для связного BaseSet, если же имеется несколько компонент связности, то ранги вычисляются для каждой из них отдельно, а затем ранг страницы умножается на относительный размер компоненты, к которой страница принадлежит. Рассчитанные таким образом ранги первоисточников пропорциональны количеству входящих (для посредников, соответственно, исходящих) дуг и потому исчезает потребность в трудоемком вычислении собственных векторов. Для улучшения работы алгоритма Р. Лемпель и С. Моран предлагали предварительно удалять часть ссылок и взвешивать остальные по тем или иным критериям.

Использование объектной модели документа. Нередко возникает ситуация, когда посредники удовлетворяют тематике запроса только некоторой своей частью, и такое положение вещей приводит к смещению тематики результатов алгоритма Клейнберга. В частности, протекционные ссылки обычно сосредоточены в некоторых местах страницы, а не разбросаны по ней хаотично.

Для разрешения этой проблемы С Чакрабарти предложил увеличить гранулярность, рассматривая вместо страницы дерево, построенное на основе объектной модели документа (Document Object Model) (DOM-дерево) (рис. 3.3).

 

 

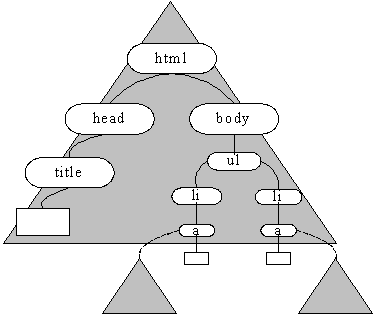
Рис. 3.3. Пример DOM-дерева

Для каждой страницы определяется граница, и поддеревья, корни которых лежат на ней, считаются неделимыми. Таким образом, один документ распадается на несколько маленьких документов. А граница, по которой происходит разбиение, определяется динамически, заново после каждой итерации. Алгоритм проведения границы основан на принципе минимальной длины описания (Minimal Description Length) относительно этой модели. Этот принцип заключается в совместной минимизации стоимости описания модели и описания реальных данных в ней. Кроме проблемы разбиения, С. Чакрабарти пришлось решать задачу пересчета рангов. Однако использовать алгоритм Клейнберга напрямую в данном случае некорректно, необходимо изменить процедуру расчета рангов посредников. Несмотря на то что теоретически сходимость такого процесса вычисления рангов не доказана, на практике он сходится достаточно быстро.

⇐ Предыдущая567891011121314Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: