Алгоритм, основанный на понятии порогового расстояния.

Пороговый алгоритм – один из самых несложных алгоритмов, базирующихся на понятии меры близости. Критерием отнесения объекта к классу здесь является пороговое расстояние Т: если объект находится в пределах порогового расстояния от точки-прототипа некоторого класса, то такой объект будет отнесен к данному классу. Если исследуемый объект находится на расстоянии, превышающем Т, он становится прототипом нового класса. Самая первая точка-прототип может выбираться произвольно. Результатом работы такого алгоритма будет разбиение объектов выборки 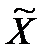 на классы, где в каждом классе расстояние между точкой-прототипом и любым другим элементом класса не превышает Т. Пороговое расстояние Т определим как половину расстояния между двумя наиболее удаленными друг от друга точками обучающей выборки.

Алгоритм пороговый

1. Выбрать точку-прототип первого класса (например, объект Х₁ из обучающей выборки). Количество классов K положить равным 1. Обозначить точку-прототип Z₁.

2. Определить наиболее удаленный от Z₁ объект Х_f по условию:

    ,

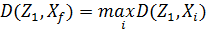где  - расстояние между Z₁ и X_i, вычисленное одним из возможных способов. Объявить Х_f прототипом второго класса. Обозначить Х_f как Z₂. Число классов К=К+1.

3. Определить пороговое расстояние .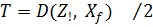

 Построить \ .

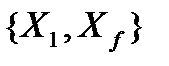4. Выбрать .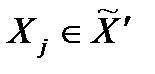

5. Вычислить расстояние от X_j до всех точек-прототипов: 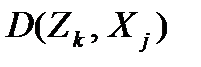для k=1, 2, …K.

6. Определить ближайшую к рассматриваемому объекту точку-прототип Z_p по условию

    .

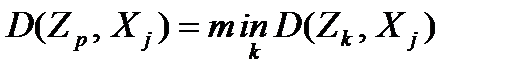7. Если 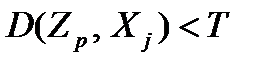, отнести объект X_j к классу p (Z_p является прототипом этого класса) и удалить его из 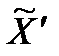. Иначе объявить X_j прототипом нового класса. Обозначить X_j как Z_К+1. Число классов К увеличить на 1: К=К+1. Удалить Xj из .

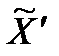8. Если 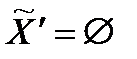 (то есть обучающее множество исчерпано), то КОНЕЦ. В противном случае перейти к шагу 4.

К достоинствам рассмотренного алгоритма следует отнести простоту реализации и небольшой объем вычислений. Очевидны также его недостатки: не предусмотрено уточнение разбиения. В результате расстояние от объекта до точки-прототипа класса может оказаться больше, чем расстояние от этого объекта до точки-прототипа другого класса. Результат, кроме того, сильно зависит от порядка рассмотрения объектов 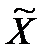, а также от способа вычисления порогового расстояния (можно использовать и другие формулы для подсчета Т). Из этого обсуждения следует, что полезно было бы использовать алгоритмы, допускающие многократную коррекцию формируемых классов, например, можно было бы менять пороговое расстояние Т и проводить многократное уточнение разбиения.

 

Алгоритм MAXMIN. Рассмотрим более эффективный по сравнению с предыдущим алгоритм, являющийся улучшением порогового алгоритма. Исходными данными для работы алгоритма будет, как и раньше, выборка 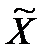. Объекты этой выборки следует разделить на классы, число и характеристики которых заранее неизвестны.

На первом этапе алгоритма все объекты разделяются по классам на основе критерия минимального расстояния от точек-прототипов этих классов (перваяточка-прототип может выбираться произвольно). Затем в каждом классе выбирается объект, наиболее удаленный от своего прототипа. Если он удален от своего прототипа на расстояние, превышающее пороговое, такой объект становится прототипом нового класса. Отметим, что в этом алгоритме пороговое расстояние не является фиксированным, а определяется на основе среднего расстояния между всеми точками-прототипами, то есть корректируется в процессе работы алгоритма. Если в ходе распределения объектов выборки 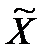по классам были созданы новые прототипы, процесс распределения повторяется. Таким образом, в алгоритме MAXMIN окончательным считается разбиение, для которого в каждом классе расстояние от точки-прототипа до всех объектов этого класса не превышает финального значения порога Т.

Для вычисления Т - порогового расстояния между К точками-прототипами воспользуемся следующей формулой. Для произвольного числа классов К пороговое расстояние считается как половина среднего расстояния между точками-прототипами, то есть

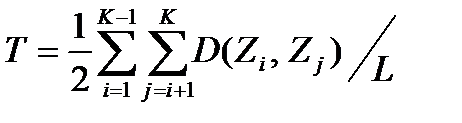, где .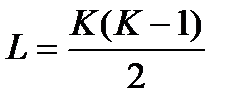

 

Алгоритм MAXMIN.

1. Выбирается первоначальная точка-прототип (например, Х₁); она становится точкой-прототипом первого класса и обозначается далее Z₁. Количество классов полагаем равным 1: К=1.

2. Определяется X_f – наиболее удаленный от Z₁ объект. X_f становится точкой-прототипом нового класса и обозначается далее Z_f. К=К+1.

3. Находим Т – пороговое расстояние.

4. Для всех объектов обучающего множества строится матрица расстояний до каждого из имеющихся прототипов: , .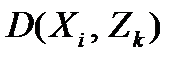

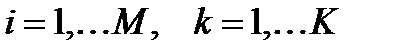5. Каждый объект относится к классу по критерию наибольшей близости к точке-прототипу: X_i отнесен к классу р, если .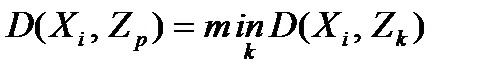

6. В каждом классе k определяется объект X_lk, наиболее удаленный от точки-прототипа: 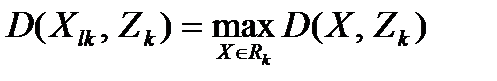, где 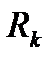- множество объектов класса k.

7. Для всех найденных объектов проверяется условие: .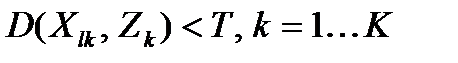

Если для некоторого 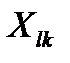это условие не выполнено, он становится точкой-прототипом нового класса, количество классов К=К+1.

 8. Если новых классов не создано, то КОНЕЦ. Иначе – перейти к шагу 9.

9. Вычисляется новое значение Т как среднее расстояние между прототипами.

10. Перейти к шагу 4.

 

     Алгоритм позволяет получить лучшее разбиение точек на классы, поскольку разбиение многократно уточняется. Это снижает чувствительность алгоритма к ошибкам в обучающем множестве, а также к выбору порядка рассмотрения объектов. Недостатком является необходимость многократно рассчитывать расстояния между точками.

Алгоритм К средних.

    Рассмотрим алгоритм, решающий задачу обучения «без учителя» при одном дополнительном условии: количество классов, к которым могут принадлежать элементы обучающей выборки, заранее известно (классов – К). В такой ситуации первоначально выбираются К точек-прототипов (например, первые К объектов обучающей выборки ). Затем все объекты обучающей выборки  распределяются по классам по критерию наименьшего расстояния от точек-прототипов этих классов. В каждом из сформированных классов определяется новая точка-прототип как " средняя" точка данного класса. Если точки-прототипы при этом изменяются, то распределение объектов по классам выполняется заново. Признаком окончания работы алгоритма здесь будет совпадение разбиений на классы на двух последовательных итерациях. В окончательном разбиении каждый объект из должен оказаться ближе к " центру", то есть к прототипу своего класса, чем к прототипу любого другого класса. Заметим также, что в алгоритме " К средних" точки-прототипы могут не совпадать ни с одним реальным объектом из , поскольку определяются как " средние" точки своих классов.

 

1. Обозначим номер итерации s=0. Выбираются К начальных точек-прототипов:

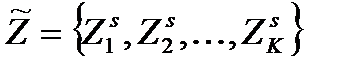 из .

    2. Выполняется итерация s=s+1.

3. Строится матрица расстояний. Каждый объект 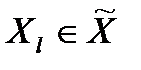относится к одному из классов  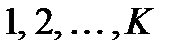по признаку ближайшего расстояния до точки-прототипа.

4. Для каждого из сформированных классов вычисляется новая точка-прототип. Для этого значение каждого признака для точки-прототипа класса k определяется как среднее арифметическое значений этого признака по всем объектам k-го класса, сформированного на текущей итерации s:

,

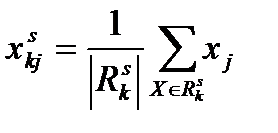где 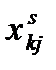- значение j-го признака для определяемой точки-прототипа класса k, 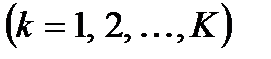, 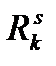- множество объектов, отнесенных к классу k на s-й итерации,  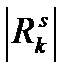- мощность этого множества. 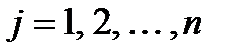, поскольку каждый объект обучающей выборки содержит n признаков.

5. Если для всех 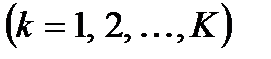верно, 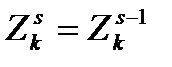, то КОНЕЦ,

иначе – переход к шагу 2.

 

Заметим, что в качестве точек-прототипов полезно брать не первые К объектов из , а максимально различные между собой объекты.

Алгоритмы, рассмотренные в этой главе, обладают одним общим свойством: с их помощью решается задача классификации для обучающей выборки , то есть строится разбиение примеров обучающей выборки на классы. Вспомним, что алгоритмы обобщения должны успешно решать и задачу распознавания, то есть распределения вновь предъявляемых примеров по классам. Последняя требует наличия четко сформулированного решающего правила, или алгоритма, позволяющего отнести новый объект Х к одному из классов.  

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: