Разделяющие решающие функции. Алгоритм построения линейной решающей функции.

Разделяющие решающие функции

Рассмотрим метод построения решающих функций как получение уравнения границ, разделяющих классы. Первоначально рассмотрим самый простой случай – случай двух классов. Тогда задача сводится к построению только одной решающей функции; такая функция должна принимать положительные значения для объектов одного класса и отрицательные – для другого класса. В случае, когда классов несколько, можно использовать различные стратегии.

Метод 1. Сначала какой-либо класс (обозначим его класс 1) считаем первым, а все остальные классы в совокупности – вторым. Найдем решающую функцию, отделяющую класс 1 от остальных. Аналогично построим функцию, отделяющую класс 2 от остальных и т. д. (рис. 4. 1). Всего построим К решающих функций. Решение о принадлежности объекта Х классу k принимается, если выполняется условие:

 для всех .

 

       x₂                                     

       -                            

       -                   

       -                                                             r   r

       -   r   r                                        r

       -        

       -   r         

       -                               r       

       -                         r r r        

       0  | | | | | | | | | |          

х₁                                           

Рис. 4. 1

В таком методе распознавания имеются неопределенные области, в которых объект не может быть отнесен ни к одному классу.

Метод 2. Находится решающая функция для разделения каждой пары классов. Количество решающих функций здесь будет равно количеству пар классов: .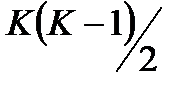

 

 

       x₂                                     

1 -3

       -                                  

       -                   

       -                                                             r   r

       -   r   r                                       r

       -        

2 -3

1-2

       -   r         

       -   1 - 2                                  r       

       -                         r r r        

       0  | | | | | | | | | |          

                                                                                                     х₁                                                       

Рис. 4. 2

Решение о принадлежности Х классу k принимается, если выполнено условие: 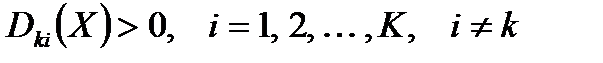. При таком подходе возможно наличие единственной области неопределенности (на рис. 4. 2 - в центре). Объекты, попадающие в эту зону, не могут быть отнесены ни к одному классу.

    Метод 3. Следующий подход основан на устранении областей неопределенности и является комбинацией методов 1 и 2 (рис. 4. 3).

 

 

 

       x₂                                     

       -                                  

       -                   

       -                                                             r   r

       -   r   r                                        r

       -        

       -   r         

       -                                     r       

       -                         r r r        

       0  | | | | | | | | | |          

                                                                                                     х₁                                                       

Рис. 4. 3

 

    Если можно построить линейные решающие функции, будем говорить, что классы линейно разделимы.

Рассмотрим алгоритм построения линейных решающих функций. Линейная функция имеет следующий вид: . Цель алгоритма – найти коэффициенты 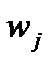 решающей функции  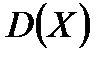методом последовательного уточнения. Рассмотрим случай двух классов (выше было показано, какими приемами можно свести к этому случаю вариант нескольких классов). Основой для вычисления коэффициентов  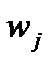является анализ обучающей выборки , где известна заранее принадлежность объектов классу 1 или классу 2. Далее эти два класса обозначим С₁ и С₂.

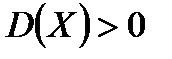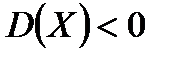Решающая функция считается построенной, если все объекты обучающей выборки распознаются этой функцией правильно, то есть , если , и, соответственно, , если 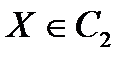. Коррекция коэффициентов решающей функции выполняется по следующему правилу: коэффициенты решающей функции увеличиваются при неправильном распознавании объекта из класса С1, уменьшаются при неправильном распознавании объекта из класса С2 и остаются без изменения, если распознавание идет правильно. Если на некотором шаге произойдет корректировка коэффициентов решающей функции, счетчик правильно распознанных объектов, обозначаемый далее как сч, сбрасывается в ноль, поскольку мы перешли к новой функции и теперь ее надо проверить на всех элементах обучающей выборки.

Алгоритм завершается, когда окажется, что построенная решающая функция D(Х) правильно распознает все объекты обучающего множества.

 

Алгоритм построения линейной решающей функции.

1. Получить обучающую выборку , элементы которой принадлежат непересекающимся классам С₁ или С₂.

2. Установить в ноль счетчик правильно распознанных объектов: сч=0.

3. Установить номер итерации равным нулю: к=0.

4. Задать начальные значения коэффициентов 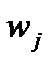в решающей функции (например, ). Получим решающую функцию .

5. Выбираем класс С₁ в качестве текущего класса.

6. Переход к новой итерации: к=к+1.

7. Выбрать очередной объект 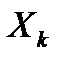текущего класса (класса С₁). Если класс С₁ исчерпан, объявить текущим классом класс С₂  выбрать первый объект этого класса.

8. Вычислить новые значения коэффициентов решающей функции на итерации к:

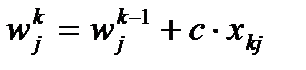, где с – множитель, определяемый из условия

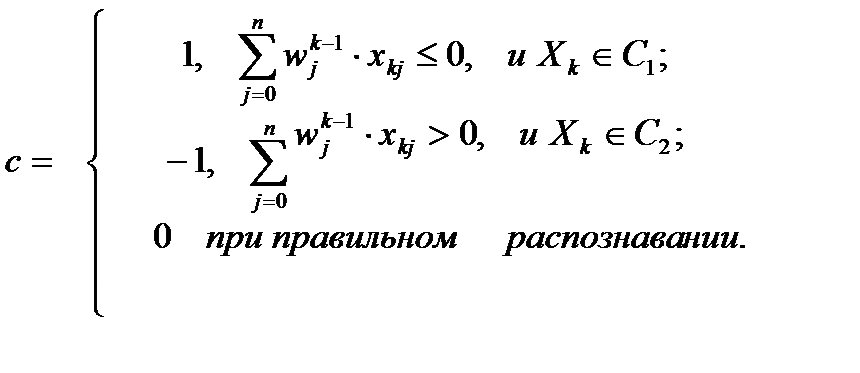
9. Если с=0, сч=сч+1 (увеличиваем на 1 число правильно распознанных объектов), иначе сч=0.

10. Если сч=М – общему числу объектов обучающей выборки , то КОНЕЦ, иначе перейти к шагу 6.

Приведенный алгоритм обеспечивает построение решающей функции во всех случаях, когда классы являются линейно разделимыми.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: