 |
Построение решающих функций методом потенциалов
|
|
|
|
Построение решающих функций методом потенциалов
Иногда точки обучающей выборки невозможно разделить, используя линейные функции. На рис. 4. 4 приведен пример такой обучающей выборки. В случае, если классы невозможно разделить линейно, используется метод потенциалов, предназначенный для построения нелинейных решающих функций.
Само название " метод потенциалов" связано со следующей интерпретацией. Предположим, что любой точке из обучающего множества соответствует некоторый объект, обладающий зарядом (наподобие электрического). Объекты разных классов имеют заряды разных знаков: положительные и отрицательные. В любой точке n-мерного пространства признаков такие заряды создадут некоторый потенциал, являющийся суммой потенциалов отдельных зарядов. Величина потенциала прямо пропорциональна величине заряда и обратно пропорциональна расстоянию до него.
x2
-
-
- r r r
- r r ª ª r - элементы первого класса
- ª ª ª - элементы второго класса -
- r r ª ª
- r r
- r r r
0 | | | | | | | | | |
х1
Рис. 4. 4
Известно, что линии, соединяющие точки с одинаковыми потенциалами, называются эквипотенциалями. В таких условиях каждый класс отделен от другого " потенциальной долиной", имеющей нулевой потенциал. Такая нулевая эквипотенциаль представляет собой границу между классами; ее уравнение и будет решающей функцией.
|
|
|
Функция, описывающая закон изменения потенциала, создаваемого зарядом, помещенным в точку Хс, может быть задана по-разному. Рассмотрим два варианта:
1) 
;
2) 
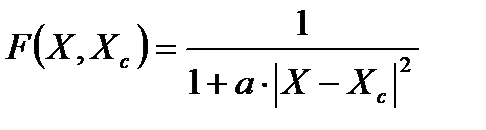, где а> 0 – константа (можно принять а=1).
Если рассматривать расстояние по Евклиду, вторая функция примет вид:
Здесь коэффициент а=1.
Рассмотрим алгоритм построения решающей функции как разделяющей границы 
, отделяющей области положительного и отрицательного потенциалов. При описании алгоритма используем обозначения, принятые в описании алгоритма построения линейной разделяющей функции. Легко заметить, что оба алгоритма имеют много общего.
Алгоритм построения нелинейной разделяющей функции
1. Получить обучающую выборку 
, элементы которой принадлежат классам С1 или С2.
2. Установить в ноль счетчик правильно распознанных объектов: сч=0.
3. Установить номер итерации равным нулю: к=0.
4. Начальное значение решающей функции 
.
5. Выбрать в качестве текущего класса класс С1.
6. Выполнение новой итерации: к=к+1. Если к > М, примем к=1.
7. Выбрать очередной объект Xk из текущего класса. Если текущий класс исчерпан, объявить текущим класс С2; выбрать из него первый объект.
8. Построить новую решающую функцию:
,
где множитель с выбирается из условий
9. Если с=0, то сч=сч+1, иначе сч=0.
10. Если сч=М, то КОНЕЦ иначе перейти к шагу 6.
Заметим, что при выполнении пункта 8 на первой итерации всегда получим значение множителя с=1, так как 
.
Лекция 13. Деревья решений
1. Понятие дерева решений.
2. Построение бинарного дерева: алгоритм ДРЕВ.
3. Алгоритм на основе метрики Хэмминга.
Дерево решений - это дерево, внутренние узлы которого представляют собой проверки для входных примеров из обучающего множества, а вершины-листы являются категориями, классами (примеров). Пример дерева решений приведен на рис. 3. 1. Дерево решений каждому входному примеру ставит в соответствие номер класса (или выходное значение) путем фильтрации этого примера через узлы проверки дерева сверху вниз. Результаты каждой проверки являются взаимоисключающими и исчерпывающими. Например, проверка T2 в дереве изображенном на рис. 4. 5 имеет три возможных исхода: самый левый относит входной пример к классу 3, средний перенаправляет входной пример вниз к проверке T4, а самый правый относит пример к классу 1. Мы будем следовать обычной договоренности об изображении узлов-листьев номерами классов.
|
|
|
Рис. 4. 5
Существует несколько характеристик, по которым деревья решений могли бы различаться:
1. Проверки могут быть многопризнаковыми (выполняется проверка нескольких признаков входного примера за раз) или одно-признаковыми (выполняется проверка только одного признака).
2. Проверки могут приводить к двум результатам или более чем к двум. (Если все проверки приводят к двум результатам, то мы получаем двоичное дерево решений).
3. Признаки (или атрибуты), которые используются в узлах дерева, могут быть качественными или количественными. Бинарные признаки могут рассматриваться как любые из них.
4. Классов может быть два или более. Если мы имеем два класса и объекты классификации представляют собой двоичные входные векторы, то дерево реализует булеву функцию и называется булевым деревом решений.
Удобно использовать дерево решений с пометками на ребрах. В нем вершины, не являющиеся концевыми, помечены именами атрибутов, ребра – допустимыми значениями соответствующего атрибута, и концевые вершины – именами классов. Процесс классификации заключается в прохождении пути из корня к листьям, следуя ребрам, соответствующим значениям атрибутов объекта.
Итак, дерево решений – это наглядная форма представления классификатора объектов. Основой для построения дерева решений является обучающее множество.
В таблице 2 приведен пример обучающего множества. Здесь каждый объект имеет четыре атрибута: класс, рост, цвет волос и цвет глаз.
|
|
|
Т а б л и ц а 2.
| Класс | Рост | Волосы | Глаза |
| – | низкий | светлые | карие |
| – | высокий | темные | карие |
| + | высокий | светлые | голубые |
| – | высокий | темные | голубые |
| – | низкий | темные | голубые |
| + | высокий | рыжие | голубые |
| – | высокий | светлые | карие |
| + | низкий | светлые | голубые |
Наблюдая примеры, приведенные в таблице, сформулируем закономерность их разделения на классы: все голубоглазые объекты с волосами, светлыми или рыжими, относятся к классу +; все темноволосые объекты, либо светловолосые, но с карими глазами, относятся к классу -. Заметим также, что признак Рост не влияет на выбор класса. Рассмотрим способы описания полученных решений в автоматизированной системе.
На рис. 4. 6 приведен пример дерева решений для обучающей выборки из таблицы 2.
Рис. 4. 6.
Еще один способ представления решающего правила - продукции.
Продукционные правила представляются в виде
если < посылка>, то < заключение>
В системах извлечения знаний в качестве посылки выступает описание объекта через его свойства, а заключением будет вывод о принадлежности объекта к определенному классу. Примером такого продукционного правила является
если pH < 6, то жидкость – кислота.
В экспертных системах часто используются правила, в которых посылкой является описание ситуации, а заключением – действия, которые необходимо предпринять в данной ситуации.
Основные достоинства, благодаря которым продукционные правила получили широкое распространение, заключаются в следующем:
1) продукционные правила легки для восприятия человеком;
2) отдельные продукционные правила могут быть независимо добавлены в базу знаний, исключены или изменены, при этом не требуется перепрограммирование всей системы. Как следствие этого, представление больших объемов знаний не вызывает затруднений;
3) с помощью продукционных правил выражаются как декларативные, так и процедурные знания.
Решающие деревья иногда более сложны для понимания человеком, чем продукционные правила, что является их недостатком. С другой стороны, любое решающее дерево может быть преобразовано в набор продукционных правил: каждому пути от корня дерева до концевой вершины соответствует одно продукционное правило. Его посылкой является конъюнкция условий атрибут–значение, соответствующих пройденным вершинам и ребрам дерева, а заключением – имя класса, соответствующего концевой вершине. Так, приведенное выше решающее дерево может быть записано в виде следующего набора продукционных правил:
|
|
|
если волосы=светлые & глаза=голубые то класс=“+”
если волосы=светлые & глаза=карие то класс=“–”
если волосы=темные то класс=“–”
если волосы=рыжие то класс=“+”.
Эти наиболее популярные модели описания класса объектов равносильны. Перейдем к рассмотрению конкретных алгоритмов, использующих такие модели.
|
|
|
