 |
Лекция 12. Решающие функции. Построение решающих функций по критерию минимального расстояния
|
|
|
|
Лекция 12. Решающие функции
1. Решающие функции.
2. Границы между классами.
3. Построение линейных РФ
4. Метод потенциалов.
5. Нелинейные РФ.
Прежде всего, необходимо дать понятие решающей функции. В системах распознавания по признакам, где любой объект распознавания представим как вектор 
, образованный значениями признаков 
, введем функцию 
от значений признаков. Пусть по значениям этой функции принимается решение об отнесении объекта к одному из известных классов (или о том, что объект не может быть отнесен ни к одному из классов). Назовем такую функцию решающей функцией.
Существуют различные способы построения решающих функций. Прежде всего решающая функция может строиться как выражение, значение которого отражает расстояние между классифицируемым объектом и классом (прототипом класса). Решающая функция может представлять собой также уравнения границ между классами. В этом случае вектор представим точкой в n-мерном пространстве признаков. При удачном выборе признаков для распознавания объекты, принадлежащие одному классу, группируются в некоторую область – кластер. Если эти области достаточно четко очерчены (классы четко разделимы), то можно построить гиперповерхности, разделяющие классы. В частном случае, когда, например, объект характеризуется только двумя признаками, моделью будет плоскость, на которой расположены точки, отображающие объекты распознавания. Разделяющие поверхности будут представлять собой кривые на плоскости. Для трехмерного случая (объект задается тремя признаками) границами между классами будут разделяющие поверхности. Задача поиска решающей функции есть задача отыскания уравнений таких поверхностей.
|
|
|
Чтобы распознать объект Х относительно классов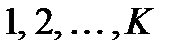 
на основе решающих функций необходимо или сравнивать расстояния между Х и прототипами заданных классов, или оценить положение Х относительно разделяющих классы гиперповерхностей.
Поскольку распознавание возможно только относительно известных классов, для решения такой задачи необходимо разбить на классы элементы обучающей выборки 
, например, с помощью одного из вышеизложенных алгоритмов, затем построить решающие функции для отнесения объекта к одному из классов. Следующий шаг – отнесение объекта Х к одному из классов на основе построенных решающих функций (непосредственно задача распознавания).
Построение решающих функций по критерию минимального расстояния
Простейшим способом распознавания некоторого объекта Х является сравнение расстояний между данным объектом и объектами-прототипами всех известных классов. Предъявляемый объект Х считается принадлежащим классу k, если выполняется условие 
, где 
- классы, 
- вектор, характеризующий объект-прототип класса i. В качестве объекта-прототипа класса можно использовать его " геометрический центр" (как в алгоритме К средних). Расстояние между предъявленным объектом Х и прототипом i-го класса Zi может быть найдено, например, как обычное евклидово расстояние:
.
Для упрощения вычислений вместо непосредственного расчета величины 
можно построить другие решающие функции, значения которых связаны определенным образом с расстоянием. Рассмотрим один из методов получения решающей функции.
Найдем квадрат расстояния между Х и прототипом Zi:
= 
= 
.
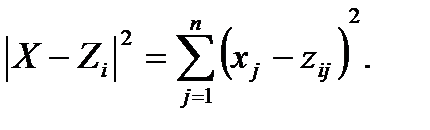В данном выражении Х – вектор–переменная, Zi – вектор–константа, ХТ - транспонированный вектор. Заметим, что произведение 
не связано с конкретным классом, и, следовательно, не внесет вклад в оценку близости двух объектов. Отбросим его, а оставшуюся часть формулы умножим на (–1). Результатом будет следующая решающая функция:
|
|
|
.
После умножения на (–1) была получена функция, принимающая максимальное значение при минимальном расстоянии от объекта Х до прототипа. Получен критерий распознавания: объект Х относим к классу k, если выполняется условие
.
Очевидно, потребуется построить К решающих функций, по одной для каждого класса. Заметим, что для К классов можно строить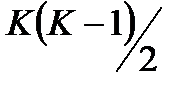 
решающих функций в случае, когда для каждой пары классов строится своя решающая функция. К достоинствам метода можно отнести также отсутствие областей неопределенности, то есть областей значений признаков, для которых объект не может быть отнесен ни к одному классу. Однако, метод хорош только если точки, соответствующие объектам класса, образуют выпуклые области.
|
|
|
