 |
Характеристики моделей процессов как объектов исследований
|
|
|
|
Подготовка любого нового производства начинается с проработки схемы, определяющей последовательность технологических операций и особенностей их протекания, что осуществляется в лабораторных условиях и позволяет в результате получить данные, которые будут характеризовать способ производства. На следующем этапе отработка параметров процесса – режимов, компоновки технологической установки, проверки отдельных конструктивно-технологических решений и т.д. осуществляется на экспериментальных образцах, являющихся моделями или прототипами будущих машин и аппаратов.
Большинство процессов пищевых производств и объектов пищевой промышленности характеризуется значительным числом взаимосвязанных факторов и случайными изменениями параметров во времени. Поэтому изучение и исследование процессов проводятся с целью:
- раскрытия сущности и закономерности процессов,
- определения оптимального режима работы объекта (аппарата или технологической машины),
- определения характеристик объекта.
Методика исследования процессов в оборудовании пищевых производств включает следующие виды работ [42]:
- изучение физических явлений в статике и в динамике;
- теоретическое и экспериментальное исследование процессов на моделях в лабораторных и производственных условиях;
- обобщение полученных данных на основе математического описания и анализа физической сущности процессов с использованием теории подобия физических явлений;
- представление результатов анализа в форме расчетных зависимостей для создания нового оборудования и определения его технико-экономических показателей.
Этап моделирования позволяет решить ряд вопросов о размерах установки, конструкции ее основных узлов, получить данные о стоимости, выходе продукции, удельных расходах сырья, удельной материалоемкости и энергоемкости.
|
|
|
Результаты исследований могут быть представлены в виде таблиц, графиков, уравнений или в численном виде, т.е. в виде математического описания процесса. Математическое описание обеспечивает предсказание хода процесса и его ожидаемых результатов. Оно используется для проверки теоретических положений. Без знания закономерностей, которым подчиняется тот или иной процесс и которые описываются расчетными формулами и получаемыми из них количественными оценками, нельзя создать современное технологическое оборудование и средства его автоматического управления и регулирования.
Для создания автоматизированного оборудования нужны данные о пределах изменения параметров процесса, т.е конечных и начальных состояниях, о закономерностях изменения этих параметров во времени, что обеспечивается уравнениями кинетики, и характере реакции на возмущающие воздействия, без чего нельзя разработать оптимальное управление.
Сущность математического описания процесса, системы или объекта заключается в получении математической модели или соответствия, связывающего характеристики входящего материала и выходящего продукта, 
, где 
- оператор, характеризующий математическую операцию преобразования входных функций 
в выходные функции 
.
Отсутствие модели и недостаточные знания динамических свойств объекта приводят к интуитивному (неоптимальному) управлению процессом и невозможности прогнозирования свойств получаемой продукции.
Математическая модель процесса является адекватной объекту, если она с приемлемой точностью отражает его поведение.
Основу классификации моделей составляют следующие признаки:
1. Число факторов, от которых зависит оператор системы и параметры процесса:
|
|
|
- если оператор или входные параметры не зависят от аргументов, то математическая модель называется статической. Этот вид моделей описывается алгебраическим уравнением 
;
- если входной параметр или оператор зависят от аргументов, то модель называется динамической;
- если входной параметр или оператор зависят только от одного аргумента, то модель называется моделью с сосредоточенными параметрами -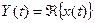 
. Этот класс моделей описывается обыкновенными дифференциальными уравнениями;
- если число независимых аргументов более одного (время и пространственные координаты), то такая модель называется моделью с распределенными параметрами - 
. Такая модель описывается дифференциальными уравнениями с частными производными.
Входные параметры процесса могут обладать свойством однородности. Параметр 
является однородным по аргументу 
, если изменение на произвольную величину 
не изменяет параметр, т.е. 
. Если аргументом, по которому однороден параметр или оператор является время, то параметр называется стационарным. Система, оператор которой стационарен, называется стационарной.
2. Природа исследуемого процесса или объекта. По данному признаку модели делятся на вероятностные и детерминированные. В вероятностных моделях учитывается случайная природа входных параметров или оператора. Примерами таких моделей являются модели смешивания сыпучих частиц различных видов. Эти модели могут быть регрессионными или корреляционными:
- если выходной параметр процесса представляет собой случайную величину, а фактор (входной параметр) является неслучайным, то математическая модель называется регрессионной, например, 
;
- если выходной и входной параметры представляют собой случайные величины с определенным законом распределения, то взаимосвязь между ними или математическая модель процесса называется корреляционной;
- в детерминированных моделях выходные параметры однозначно определяются факторами и оператором процесса.
3. Свойство линейности модели. Математическая модель называется линейной, если линеен оператор системы. Оператор называется линейным, если выполняется принцип суперпозиции (равенство) 
, где 
- приращение фактора.
|
|
|
Методы получения моделей процессов подразделяются на теоретические и экспериментальные [2].
Теоретический метод заключается в анализе физической сущности процесса с использованием общих законов физики или в составлении уравнений материального или энергетического баланса.
Экспериментальный метод математического описания процесса или объекта заключается в обработке экспериментальных данных.
Наиболее эффективным способом получения той или иной модели является сочетание теоретического и экспериментального методов, где теоретический анализ затрагивает в основном структурные свойства объекта и получение уравнений, а на долю экспериментального метода приходится количественный анализ по определению численных значений коэффициентов уравнений и проверка теоретических выводов.
Одним из основных средств экспериментального изучения объектов являются методы, использующие математическую статистику (дисперсионный анализ и др.). При экспериментальных исследованиях производственных процессов и объектов, находящихся в непрерывной эксплуатации, возникает ряд сложностей, обусловленных:
- большим числом взаимосвязей факторов;
- высоким уровнем помех, природа которых носит случайный характер;
- трудоемкостью обработки данных;
- нарушением нормального режима работы объекта.
Экспериментальные методы получения моделей могут быть пассивными и активными. При пассивном эксперименте информация о параметрах процесса получается путем регистрации и наблюдения без какого–либо воздействия на исследуемый объект со стороны наблюдателя. При активном эксперименте информацию о параметрах процесса получают путем направленного изменения входных факторов в соответствии с составленным планом эксперимента.
В реальных условиях эксплуатации объекта активный эксперимент не всегда возможен, поскольку может привести к браку продукции и дестабилизации технологического процесса.
Общим недостатком обоих методов получения информации о процессе или объекте является то, что получаемые с их помощью модели приемлемы лишь в диапазоне варьирования (изменения или существования) исследуемых факторов. Экстраполяция экспериментально построенной модели одного процесса на другой, даже полностью аналогичный, как правило, некорректна.
|
|
|
При получении статических моделей используются следующие методы:
- в пассивном эксперименте – регрессионный и корреляционный анализ, метод последовательного исключения функций;
- в активном эксперименте – факторные планы.
Для получения динамических моделей используются:
- в пассивном эксперименте – корреляционный, спектральный и динамический регрессионный анализ;
- в активном эксперименте – методы пробных возмущений.
Выбор метода получения модели определяется показателями процесса и объекта, задачами исследования и условиями применения метода.
|
|
|
