 |
Основные положения теории подобия. Метод анализа размерностей.
|
|
|
|
Из большого спектра инженерных задач по исследованию технологических процессов и аппаратов пищевых производств обширный класс составляют задачи, в которых требуется определить параметры той или иной операции процесса из составленных исследователем уравнений, описывающих данный процесс. При теоретических исследованиях, когда для нахождения количественных зависимостей используются общие законы физики, их приложение к исследуемым явлениям позволяет получать и общие связи между параметрами явления и применять их для решения широкого класса задач. Примером может служить дифференциальное уравнение второго порядка, описывающее явление теплопроводности 
. Это уравнение не содержит конкретных значений отдельных величин, а только характеризует общую связь между величинами и поэтому может быть использовано для описания свойств целого класса явлений теплопроводности. Отсюда следует, что любое дифференциальное уравнение является математической моделью явлений с одинаковой физикой протекающих процессов. При этом следует иметь в виду, что по форме уравнения могут быть идентичными, однако по физическому содержанию описывать совершенно другой класс явлений. Примером может служить дифференциальное уравнение нестационарного процесса переноса вещества 
, которое по форме одинаково с уравнением теплопроводности, но служит для описания другого класса явлений.
Из теории дифференциального исчисления известно, что интегрирование любого дифференциального уравнения дает бесчисленное множество различных решений [9]. Для получения частного решения необходимо задать определенные условия, которые должны однозначно определять единичное явление. Эти условия называются условиями однозначности и содержат все особенности данного конкретного явления.
|
|
|
Условия однозначности состоят из геометрических условий, характеризующих форму и размеры объекта, физических условий и граничных условий, характеризующих взаимодействие объекта с окружающей средой, а также временных условий для нестационарных процессов.
Таким образом, конкретное единичное явление полностью определяется дифференциальным уравнением с четырьмя условиями однозначности.
На практике очень часто встречаются ситуации, когда найти решение, которое удовлетворяло бы дифференциальному уравнению и условиям однозначности, невозможно. В этом случае целесообразно объединение экспериментального и математического методов в одну систему. Такое объединение может быть осуществлено на основе теории подобия, которая позволяет сделать определенные выводы из математической модели с условиями однозначности без интегрирования составленных уравнений и подводит теоретическую базу для получения экспериментальных данных и их обработки.
В теории подобия, кроме класса и единичного явления, используется понятие группы явлений, под которой понимается совокупность процессов, описываемых одинаковыми по форме и содержанию уравнениями и одинаковыми по форме и содержанию условиями однозначности. То есть различие между процессами будет состоять только в различии численных значений величин, входящих в условия однозначности. Группа явлений выделяется путем умножения каждой величины, входящей в условия однозначности, на постоянные численные множители.
Геометрическое подобие. Из рис. 1.3 видно, что известные геометрические условия могут быть записаны следующим образом: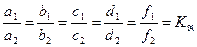 
, или в общем виде 
. То есть для двух геометрически подобных фигур отношение сходных линейных размеров есть величина постоянная. Эта величина обозначается 
и называется множителем масштабного преобразования.
|
|
|
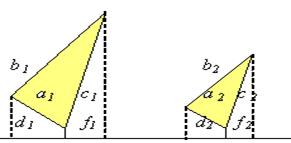
Рис. 1.3. Геометрическое подобие фигур
Площади поверхности фигур будут относиться друг к другу как квадраты их линейных размеров: 
или 
. Аналогично для объемов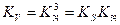 
.
Для геометрически подобных фигур имеется еще одно свойство, называемое инвариантностью подобия: отношение (инвариант подобия) между двумя любыми величинами, имеющими одинаковую размерность для одной системы, равно отношению соответствующих величин другой системы: 
.
Физическое подобие. Принципы подобия приложимы также к физическим явлениям. Константы подобия одинаковы для конечных и бесконечно малых величин, т.е. 
. После перехода к пределу 
.
Нахождение констант подобия рассмотрим на примере уравнения, выражающего условия теплообмена на границе двух сред 
.
Для сходственных точек двух подобных систем:
- первая система 
;
- вторая система 
.
Константы подобия:
, где 
- характерный размер системы.
Или 
и т.д., подставив эти выражения в уравнение для второй системы, получим 
.
Из условия тождественности уравнений следует, что 
, т.е выбор комплекса констант подобия ограничен условием, что любая их комбинация должна равняться единице.
Заменив значения констант подобия, можно получить безразмерные соотношения параметров, характеризующих процесс. В данном случае 
. Такие соотношения называются числами подобия. Полученное выше равенство называется числом Нуссельта и обозначается индексом 
.
Отношения двух однородных, т.е. имеющих одинаковое содержание и размерность, величин называется симплексом.
Для характеристики подобия используются константы и числа подобия. Константы сохраняют числовое значение только для двух подобных явлений, но остаются одинаковыми для всех сходственных точек изучаемых систем. Числа подобия сохраняют свое значение в сходственных точках всех подобных систем, но в различных точках данной системы могут иметь разные числовые значения.
Безразмерные числа подобия – это новые переменные, позволяющие уменьшить число величин под знаком функции. Количественная связь между числами подобия определяется экспериментальным путем. Направление хода эксперимента определяется с помощью теорий размерности и подобия. Теория размерности применяется при неизвестных связях между переменными, когда рассматриваются новые процессы, не имеющие аналитического описания.
|
|
|
После выбора существенных размерных величин, влияющих в наибольшей степени на исследуемый процесс, находят безразмерные комплексы и составляют уравнения подобия без составления дифференциальных уравнений и условий однозначности.
В основе теории подобия физических явлений лежат три теоремы подобия:
- первая теорема: у подобных явлений индикаторы подобия равны единице, т.е. у подобных явлений числа подобия численно равны. Первая теорема устанавливает связь между константами подобия и позволяет вывести уравнения для чисел подобия. Она указывает, что при выполнении опытов необходимо и достаточно измерять лишь те величины, которые входят в числа подобия изучаемого явления.
Пусть в двух подобных системах [42] происходит подобное движение тел. В соответствии со вторым законом Ньютона можно записать 
, т.е. для первой системы 
и аналогично для второй системы 
. Поскольку эти две системы отличаются друг от друга только масштабом, то 
; 
. Разделим уравнения движения одно на другое 
(1) или 
. Следовательно при подобии двух систем 
. Комплекс множителей данного преобразования 
называется индикатором подобия и для двух подобных явлений он равен единице. Из уравнений (1) следует, что 
и 
. Из этих записей следует вывод, что для двух подобных явлений данного класса сохраняется числовое равенство величин 
, что записывается как 
(неизменно) или 
(одно и то же). Этот комплекс величин носит название критерия Ньютона (
).
Таким образом, для ряда подобных процессов будет справедливо равенство 
. Если подобные процессы происходят в реальном образце и в его модели, то очевидно 
.
Правильность составления критериев проверяется подстановкой размерностей величин. В данном случае 
, т.е. размерности сокращаются. Критерии подобия являются безразмерными величинами. Отсюда следует, что необходимым условием получения какого-либо безразмерного критерия подобия является наличие исходного уравнения, описывающего исследуемый процесс, причем это уравнение может быть выражено в любой форме (алгебраической или дифференциальной).
|
|
|
- вторая теорема: если физическое явление описывается системой дифференциальных уравнений, то всегда существует возможность представления их в виде уравнений подобия. Из этой теоремы следует, что если результаты любого эксперимента обработать в числах подобия, то зависимость между ними надо выражать в виде уравнения подобия, которое представляет зависимость между величинами, характеризующими явление, в виде чисел подобия. Т.е. критерий подобия 
, содержащий определяемую величину, может быть выражен в виде функции других критериев, отражающих другие стороны исследуемого процесса. Вид этой функции заранее неизвестен и определяется при обработке экспериментальных данных. Результаты опытов обычно представляются в степенном виде 
, или в экспоненциальной форме 
, где 
- постоянные, определяемые при графической обработке опытных данных; 
- начальное значение критерия 
при 
; 
- время от начала процесса;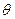 
- постоянная времени процесса, зависящая от условий его проведения.
Пример. Требуется найти вид функции 
, если есть основания считать, что зависимость между переменными является степенной, т.е. 
. Прологарифмируем данное уравнение, получим 
. Это уравнение представляет собой прямую вида 
., где 
представляет собой угловой коэффициент прямой, а величина 
определяет точку на оси ординат, через которую проходит логарифмическая прямая.
Пусть в результате проведения серии опытов получены следующие числовые значения: 
и 
. Построим прямую в логарифмических координатах и найдем неизвестные значения и 
.
Рис.1.4 График функции в логарифмических координатах
- третья теорема: подобны те явления, условия однозначности которых подобны и числа подобия численно одинаковы. Третья теорема исходит из предположения, что явления протекают в геометрически подобных системах. Если условия однозначности подобны и определяющие числа подобия равны, то отсюда вытекает равенство всех остальных определяемых чисел подобия, что имеет большое значение для обобщения результатов опыта.
Таким образом, теория подобия дает общие указания и устанавливает пути анализа уравнений, описывающих исследуемые явления.
Как подчеркивается в [42], многообразие критериев, с помощью которых могут быть описаны процессы пищевых производств затрудняет их классификацию. Для каждого из процессов разработана своя система критериев, с помощью которой составляются критериальные уравнения.
|
|
|
Существуют критерии геометрического, механического, диффузионного, термодинамического подобия и др.
Так, критерии геометрического подобия выступают в форме относительных размеров исследуемой системы, например, 
- относительная длина трубопровода, т.е. длина трубопровода, измеренная его диаметром, или 
- относительный шаг трубного пучка в цилиндрическом теплообменнике.
Гидромеханическое подобие характеризуется рядом критериев, полученных из критерия механического подобия Ньютона – это критерии Рейнольдса, Эйлера, Фруда, Галилея
Известно, что аналитическое решение системы дифференциальных уравнений, описывающих явление теплоотдачи, состоящей из отдельных дифференциальных уравнений теплообмена между твердым телом и средой, энергии потока движущейся жидкости или теплопроводности, движения вязкой жидкости и сплошности вместе с условиями однозначности наталкивается на значительные трудности из-за большого количества переменных. Эти трудности можно снять использованием теории подобия, позволяющей объединить размерные физические величины в безразмерные комплексы, рассматриваемые в качестве новых переменных. Такими комплексами для данной системы уравнений будут:
- число подобия гидродинамической гомохронности, характеризующее скорость изменения поля скоростей движущейся жидкости во времени, 
;
- число Фруда, определяющее отношение сил инерции и сил тяжести,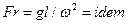 
. Этот критерий используется в расчетах мешалок, циклонов, центрифуг;
- число Эйлера, характеризующее соотношение между силами давления и силами инерции, 
. Этот критерий входит в уравнение для определения потерь напора в потоке жидкости и является мерой отношения перепада статического давления к его динамическому напору;
- число Рейнольдса, представляющее отношение сил инерции к силам вязкости и определяющее характер течения жидкости, 
.
Из уравнений энергии потока жидкости получаются следующие числа подобия:
- число Фурье, характеризующее связь между скоростью изменения температурного поля, физическими параметрами и размерами объекта, 
;
- число Пекле, являющееся числом подобия конвективного теплообмена, 
. Если в число Пекле вместо коэффициента теплопроводности 
подставить его значение 
и помножить числитель и знаменатель на избыточную температуру, то 
, где числитель характеризует теплоту, переносимую конвекцией, а знаменатель – теплоту, переносимую теплопроводностью.
Из уравнений теплообмена следуют числа подобия:
- число Нуссельта, характеризующее конвективный теплообмен между жидкостью и поверхностью твердого тела, 
, где - коэффициент теплоотдачи теплоносителя;
- число Био, 
, где - коэффициент теплоотдачи твердого тела.
Физические свойства жидкости определяются числом Прандтля, 
.
При исследовании теплообмена в свободном потоке жидкости используют число Фруда, исключая из него скорость 
, которую сложно определить, для чего умножают это число на квадрат числа Рейнольдса получая тем самым число Галилея, 
, характеризующее соотношение силы тяжести и силы молекулярного трения. Критерий Галилея характеризует случаи стекания жидкости по поверхности и встречается в уравнения теплоотдачи при конденсации пара.
Число Архимеда получают умножением числа Галилея на симплекс 
, где 
- плотности жидкости в двух точках, 
, определяющее условия свободного движения среды.
Для случая изменения плотности жидкости в разных ее точках вследствие различия температуры симплекс заменяют величиной 
, где 
- коэффициент объемного расширения среды. В этом случае число Архимеда превращается в число Грасгофа,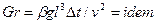 
, характеризующее соотношение подъемной силы и силы молекулярного трения.
Нетрудно видеть, что числа 
тождественны. Это различные виды одного и того же числа.
Уравнения подобия определяют зависимость между каким-либо числом подобия и другими определяющими числами подобия. Например, при тепловом расчете какого-либо аппарата искомыми величинами являются коэффициент теплоотдачи и гидравлическое сопротивление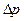 
. Конвективный теплообмен характеризуется пятью числами подобия: 
. Здесь число 
включает неизвестный коэффициент теплоотдачи , число 
- искомую величину гидравлического сопротивления при движении жидкости 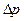. Эти два числа являются определяемыми, а остальные три – определяющими. Уравнения подобия в данном случае представляются в следующем виде:
Зависимость между числами подобия определяется экспериментальным путем. Эти исследования могут быть проведены на образце или на модели. Условия, которым должна удовлетворять модель и протекающий в ней процесс, определяются с помощью теории подобия. Поскольку подобные друг другу явления некоторой группы представляют одно и тоже явление в различных масштабах, то выводы можно распространить на все явления этой группы. Чтобы модель стала идентичной образцу, требуется выполнение следующих условий:
- процессы в натуре и в модели должны иметь одну и ту же природу и описываться одинаковыми аналитическими зависимостями;
- условия однозначности должны быть одинаковыми, кроме численных значений постоянных.
Условия однозначности требуют:
- геометрического подобия образца и модели;
- подобия условий движения продукта во входных сечениях образца и модели;
- подобия физических параметров в сходственных точках образца и модели;
- подобия температурных полей на границах среды.
Рассмотрим несколько примеров вычисления численного значения критериев
Пример: Требуется вычислить критерий Рейнольдса 
для случая движения раствора по трубам цилиндрического теплообменника, если диаметр трубы составляет 0,04м, скорость движения раствора 1,5 м/с, массовая концентрация раствора 15%, температура 1000С.
Относительная плотность раствора при данной концентрации и температуре будет равна 1,026, вязкость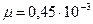 
н∙сек /м2
.
Пример: Требуется определить критерий Прандтля 
для сливок жирностью 10%, если удельный вес сливок 1,03 кг/дм3, удельная теплоемкость 
Дж/кг град, коэффициент вязкости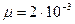 
н∙сек /м2, коэффициент теплопроводности 
Дж/м∙сек∙град.
.
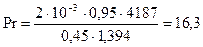Метод анализа размерностей. В случае, когда исследуемый процесс не имеет еще аналитического описания, критериальное уравнение может быть составлено с помощью метода анализа размерностей на основе использования теоремы, гласящей, что всякое уравнение, связывающее 
физических и геометрических величин, размерность которых выражена через основных единиц измерения, может быть преобразовано в уравнение подобия, связывающее 
критериев, где 
. Теорема определяет число критериев, входящих в критериальное уравнение.
Пример. Требуется исследовать процесс движения вязкой массы по трубопроводу дозатора установки для фасования продукта. Непосредственные наблюдения позволяют предположить, что необходимый перепад давления 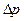зависит от скорости движения массы , ее вязкости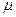 
, длины трубопровода , плотности массы 
, диаметра трубопровода 
, а также от ускорения силы тяжести 
, т.е. является функцией 
. Здесь 
.
1.Представим зависимость в степенном виде и запишем размерности величин
(1)
;
;
;
;
;
;
В размерность входит масса 
, длина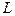 
, время 
. 
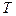и 
, т.е. критериальное уравнение должно содержать 4 критерия.
2. Заменим в уравнении (1) соответствующие величины их размерностями
или 
.
Преобразуя, получим 
. Приравняв показатели при одинаковых основаниях, получим систему уравнений
Подставим эти значения в уравнение (1)
. Объединяя отдельные величины по степеням, получим
или в обозначениях критериев 
.
Коэффициент и показатели степени 
находятся экспериментальным путем.
Условные обозначения
-выходной параметр процесса
- оператор, характеризующий математическую операцию преобразования входных функций в выходные
- входные факторы
- приращение фактора
- показатель эффективности процесса (операции)
- система критериев оптимальности
- возмущающие воздействия (случайные факторы)
- область допустимых решений
- число подобия гидродинамической гомохронности, характеризующее изменение поля скоростей движущейся жидкости во времени.
- число Фруда, характеризующее соотношение сил инерции и сил тяжести.
- число Эйлера, характеризующее сил давления и сил инерции.
Re - число Рейнольдса, характеризующее соотношение сил инерции и вязкости.
- число Фурье, характеризующее скорость изменения температурного поля.
- число Пекле, характеризующее конвективный теплообмен.
- число Нуссельта, характеризующее конвективный теплообмен между жидкостью и поверхностью твердого тела.
Pr – число Прандтля, характеризующее определенные свойства жидкости.
- число Био, характеризующее соотношения теплоотдачи сред.
- число Галилея, характеризующее соотношения сил тяжести и сил молекулярного трения.
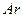- число Архимеда, характеризующее условия свободно движущейся среды.
- число Грасгофа, характеризующее соотношение подъемной силы и силы молекулярного трения.
- множитель масштабного преобразования геометрически подобных фигур.
Глоссарий
Технологический процесс -часть производственного процесса, содержащая действия по изменению и последующему определению состояния предмета производства.
Операция – всякая система действий, объединенных единым замыслом и направленная на достижение конкретной цели.
Математическая модель процесса - соотношение 
, связывающее в математической форме параметры входящего материала и выходящего продукта.
Статическая модель – модель, у которой оператор или входные параметры не зависят от аргументов.
Динамическая модель - модель, у которой оператор или входные параметры зависят от аргументов.
Модель с сосредоточенными параметрами – модель, у которой параметры процесса или оператор зависят только от одного аргумента.
Модель с распределенными параметрами -модель, у которой параметры процесса или оператор зависят от нескольких аргументов.
Однородность параметра – свойство, при котором входной параметр является по i-му аргументу, если изменение этого аргумента на произвольную величину не меняет данный параметр
Вероятностная модель – модель, у которой учитывается случайная природа входных факторов или оператора.
Линейная модель – модель, у которой линеен оператор системы и для которой выполняется принцип суперпозиции
Активный эксперимент – эксперимент, при котором информацию о параметрах процесса получают путем направленного изменения входных параметров в соответствии с планом эксперимента.
Область допустимых решений – совокупность ограничений, накладываемых на неизвестные величины.
Управление процессом – целенаправленное воздействие на параметры процесса.
Показатель эффективности – количественный критерий, позволяющий сравнивать различные решения и выбирать и них наиболее эффективное.
Прямая задача – задача исследования операций, определяющая показатель эффективности.
Обратная задача – задача определения условий, при которых показатель эффективности принимает экстремальное значение.
модель, у которой оператор или входные параметры не зависят от аргументов.
Многокритериальный процесс – процесс, характеризуемый несколькими показателями эффективности.
Числа подобия – безразмерные соотношения параметров, характеризующие процесс.
Уравнения подобия – уравнения, определяющие зависимость между одним числом подобия и другими определяющими числами подобия.
Условия однозначности – условия, определяющие особенности какого-либо единичного явления с позиций геометрических и физических параметров, взаимодействий с окружающей средой.
Симплекс – отношение двух однородных, имеющих одинаковое содержание и размерность величин.
Первая теорема подобия – теорема, устанавливающая связь между константами подобия и гласящая, что у подобных явлений числа подобия численно равны.
Вторая теорема подобия – теорема, гласящая, что физические явления, описываемые системой дифференциальных уравнений, можно представить в виде уравнений подобия.
Третья теорема подобия – теорема, гласящая, что подобны те явления, условия однозначности которых подобны и числа подобия численно равны
Критериальное уравнение – уравнение для параметров процесса на основе определяющих критериев, найденных экспериментальным путем.
Контрольные вопросы
1.Что понимают под технологическим процессом производства пищевой продукции?
2.Что понимается под математической моделью процесса?
3.По каким признакам классифицируются модели?
4.Какие существуют способы получения моделей?
5.В чем заключаются основные сложности реализации активного эксперимента в условиях реального производства?
6.Какими условиями определяется выбор того или иного метода получения модели процесса?
7.Что понимается под операцией и под термином «исследование операций»?
8.В чем состоит цель исследования операций?
9.Из каких основных этапов состоит процесс исследований операций?
10.На какие виды делятся задачи исследования операций?
11.Какие методы решения рекомендуются для многокритериальных задач?
12. Какие условия лежат в основе теории подобия?
13.Что понимается под числами и уравнениями подобия?
14. В чем заключается сущность теорем подобия?
15.Какими числами подобия описывается конвективный теплообмен?
16.В каких случаях рекомендуется применять метод анализа размерностей?
Тесты для самопроверки
1.Технологический процесс:
+а – является частью производственного процесса
б – включает в себя производственный процесс
в – является частью операции преобразования сырья в готовую продукцию
2.Проектирование технологического процесса в общем виде осуществляется в следующей последовательности:
+а - сырье - оборудование - режим обработки - анализ затрат - конечный вариант
б – анализ затрат – оборудование – режим обработки – сырье – конечный вариант
в – оборудование – режим обработки – сырье – анализ затрат – конечный вариант
г – режим обработки – оборудование – анализ затрат – сырье – конечный вариант.
3.Математическая модель является адекватной процессу, если:
а - погрешность между моделью и реальным процессом составляет не более 0,05
+б – отражает поведение процесса с приемлемой точностью
в – точно описывает только один основной параметр процесса.
4.Математическая модель процесса является статической, если:
+а – оператор и входные факторы не зависят от аргументов
б – оператор и входные факторы зависят от аргументов
в – входные факторы зависят только от одного аргумента
5.Модель процесса относится к регрессионной модели, если:
а – выходной параметр является неслучайной величиной, а входные факторы носят случайный характер
+б – выходной параметр представляет собой случайную величину, а входные факторы являются детерминированными
в – если выходной параметр и входные факторы являются случайными величинами.
6.При проведении пассивного эксперимента информацию о процессе:
+а – получают путем наблюдения за его ходом
б – путем наблюдения за ходом процесса при небольших воздействиях на исследуемый объект
в – при первоначальном воздействии на процесс без последующего вмешательства.
7.Оптимальность процесса обеспечивается:
а - при щадящих режимах эксплуатации
б – при достижении максимального выхода продукции
+в – в точках экстремальных значений заданной целевой функции, описывающей процесс.
8.Прямые задачи исследования операций отвечают на вопрос:
а – как выбрать решение, чтобы показатель эффективности процесса обратился в экстремум
+б – чему будет равен при данном решении выбранный показатель эффективности.
9.Теория подобия:
+а – позволяет получить выводы из математической модели с условиями однозначности без интегрирования уравнения
б – позволяет получить однозначное решение путем составления дифференциального уравнения, описывающего данный процесс
в – позволяет использовать для решения алгебраическое уравнение.
10. Геометрическое подобие означает, что для двух геометрически подобных фигур:
а –поверхности сходственных фигур относятся друг к другу как линейные размеры
+б – отношение сходственных линейных размеров есть величина постоянная
в – объемы геометрически подобных фигур относятся друг к другу как площади их поверхностей.
11.Инвариант подобия означает:
+а – отношение двух любых величин с одинаковой размерностью для одной системы равно отношению соответствующих величин др
|
|
|
