Основные принципы исследования процессов

При протекании процессов происходит взаимодействие тел, например, обрабатываемой среды и рабочего органа, компонентов между собой и др. Взаимодействия могут носить механический, тепловой или диффузионный характер. Взаимодействующие между собой тела образует систему. Системы делятся на однородные (с одинаковыми свойствами) и неоднородные. Предоставленные сами себе системы всегда стремятся к устойчивому состоянию, которое характеризуется наименьшим уровнем энергии на поддержание такого состояния. Системы, находящиеся в состоянии равновесия, называются равновесными системами. Примером равновесной системы может служить однородная жидкая среда, у которой давление и температура одинаковы во всех ее частях. Для вывода системы из состояния равновесия необходимо затратить определенную энергию.

Согласно принципу Ле-Шателье в системе, выведенной из состояния равновесия, происходят изменения, направления которых противоположны силам, выводящим систему из равновесия. Применение данного принципа позволяет выяснить реакцию системы на изменение, например, давления, температуры или концентрации.

Кинетика протекания многих процессов подтверждает, что скорость протекания процесса пропорциональна величине движущей силы процесса и обратно пропорциональна сопротивлению. Приведем для иллюстрации несколько примеров разнородных процессов, кинетические уравнения которых могут быть сведены к одному общему виду [42].

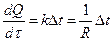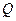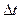Известное из термодинамики выражение для скорости передачи тепла имеет вид , где - количество тепла, - время, - движущая сила процесса перехода тепла, выражаемая в градусах (разность температур), 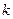- коэффициент теплопередачи, - сопротивление переходу тепла.

Для диффузионного процесса, описывающего переход массы можно записать уравнение , где - количество переданной массы вещества за время ; - коэффициент пропорциональности, характеризующий интенсивность передачи массы; - сопротивление передаче массы; 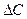- движущая сила процесса (разность концентраций веществ).

Аналогично для процесса фильтрации кинетическое уравнение будет иметь вид 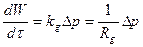, где - количество фильтрата за время ; 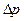- движущая сила процесса фильтрации (разность давлений); 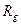- гидравлическое сопротивление фильтра и осадка, .- коэффициент пропорциональности, характеризующий проводимость фильтрующей среды.

Приведенные выше кинетические уравнения могут быть приведены к одному и тому же виду , где - оператор скорости процесса; - движущая сила процесса; 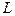- скалярная величина, характеризующая величину проводимости и обратно пропорциональная сопротивлению.

Использование аналитических методов при решении технологических, задач предполагает описание изучаемых процессов и систем определенными математическими соотношениями.

Изучение процессов должно проводиться не только в конечных состояниях в статике, но и во времени, т.е. в динамике. Совместное изучение статики (условий равновесия), кинетики (характера движущих сил) и динамики процессов (изменения параметров во времени) позволяет глубже установить взаимосвязи в ходе выполнения процесса и выбрать оптимальные параметры.

Реальные системы относятся к сложным многопараметрическим объектам с изменяемыми параметрами. Эти системы подвергаются различным внешним и внутренним возмущениям, поэтому их математическое описание представляет сложную задачу. Поэтому для формального описания используются более простые математические модели процессов. Любая математическая модель строится по некоторой общей схеме:

- технико-экономическая система представляется как совокупность более мелких подсистем и объектов;

- каждый объект характеризуется множеством наборов чисел, указывающих, например, на выпущенный объем продукции, потребленные ресурсы и т.п. Математические соотношения, описывающие это множество, называются локальными ограничениями, характерными только для данного процесса или объекта;

- соотношения, описывающие внешние связи, называются глобальными ограничениями;

- модель должна включать описание цели.

Все разнообразие задач, возникающих при управлении системой, в которой реализуются те или иные процессы, можно условно разбить на два класса:

- задачи планирования – составления плана функционирования объекта, содержащие идентификацию всех потоков продукции с учетом ограничений и цели. Данная модель должна быть простой. Этому требованию отвечают линейные детерминированные модели. Получаемые в этом случае результаты рассматриваются как ориентировочные и должны уточняться в процессе выполнения плана;

- задачи управления, заключающиеся в достижении целей всей системы.

Оптимальность плана означает минимизацию или максимизацию значений некоторой функции. Нахождение экстремума функции является классической задачей математического анализа, когда переменные могут изменяться во всем пространстве без каких-либо ограничений. Если функция непрерывно дифференцируема, то экстремальные значения будут в точках, в которых обращаются в нуль все частные производные функции. Однако на практике область переменных имеет ограничения в виде неравенств, например, ресурс -го сырья ограничен такой-то величиной и т.п., поэтому в отличие от классической задачи математического анализа речь идет об условном экстремуме функции, когда ее производные не обращаются в нуль.

В самых разных областях инженерной практики, в т.ч. при проведении исследований процессов пищевых производств, имеются задачи, обладающие рядом общих признаков, сходные по постановке и методам решения. Эти задачи объединяются под общим термином – задачи исследования операций. Например, типичная ситуация в общем случае может быть сформулирована так: организуются какие-то действия, которые можно выполнить различными способами, и надо выбрать определенное решение из ряда возможных вариантов. Исходя из такой формулировки, исследование операций будет представлять собой инструмент выявления, анализа и решения различных проблем в сложных системах [3,4,5].

Задачи исследования операций делятся на два вида: прямые и обратные. Прямые задачи отвечают на вопрос: что будет, если в заданных условиях принято какое-то решение , и чему будет равен при данном решении выбранный показатель эффективности процесса . Обратные задачи отвечают на вопрос: как выбрать решение , чтобы показатель эффективности обратился в экстремум.

В общем виде задача формулируется следующим образом: пусть имеется некий процесс, в котором реализуется некая операция 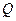, на исход которой можно влиять, выбирая тем или иным способом решение (здесь не число, а группа параметров). При известных условиях операции, т.е. не содержащих неопределенности, все факторы, от которых зависит исход, можно разделить на две группы:

- заданные факторы ;

- зависящие от субъекта элементы решения, образующие в совокупности решение .

Первая группа факторов содержит ограничения, которые определяют область возможных решений . Показатель эффективности зависит от обеих групп факторов, .

Обратная задача формулируется следующим образом: при заданных условиях надо найти такое решение , которое обращает показатель эффективности в максимум 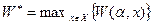. На практике задачи исследования операций, помимо двух групп факторов, содержат еще одну группу 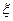- неизвестные или неконтролируемые факторы, т.е. . Наличие случайных факторов переводит задачу о выборе решения в условиях неопределенности и любое решение, принимаемое при этом, будет хуже решения, принятого при заранее известных условиях. В этом случае к точности решения нельзя предъявлять слишком высоких требований. Вместо одного единственного решения лучше выделить область решений 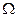, которые оказываются несущественно хуже других. В пределах этой области и должен проводиться выбор окончательного решения.