 |
Условия термодинамического равновесия при сушке.
|
|
|
|
Состояние системы «влажное тело – газ» является равновесным, если оно не изменяется во времени под действием как внутренних, так и внешних факторов.
Если влажное тело находится в равновесии с газом – смесью паров испаряемой жидкости и воздуха, то при этом происходят взаимообратные процессы испарения и конденсации, т.е. равновесие носит динамический характер. Чтобы не происходили процессы переноса жидкости или пара под действием механических причин, должно быть установлено механическое равновесие. Для этого необходимо равенство сил, действующих на границе раздела сред. Если границей раздела будет являться плоскость, то равенство сил сводится к равенству давлений по обе стороны границы. Если граница раздела будет представлять собой искривленную поверхность, то равенство давлений нарушится действием сил поверхностного натяжения.
Для устойчивого равновесия должно соблюдаться и тепловое равновесие. Кроме того, должно выполняться еще одно условие, запрещающее фазовые превращения жидкости в газ. Таким условием является равенство химических потенциалов  жидкой и газообразной фаз, т.е.
жидкой и газообразной фаз, т.е.  . Величина
. Величина  зависит от концентрации вещества в фазе.
зависит от концентрации вещества в фазе.
Таким образом, в устойчивом равновесном состоянии системы «влажное тело – смесь паров влаги с теплоносителем» должно выполняться механическое и тепловое равновесие и равенство химических потенциалов влажного тела и газа.
Исследование равновесного состояния влажного материала с газом является важным для определения движущей силы процесса сушки. Равновесное состояние системы характеризуется изотермами сорбции- десорбции, которые представляют собой зависимости равновесного влагосодержания материала от равновесной относительной влажности в процессе сорбции или десорбции при постоянной температуре.
|
|
|
Сорбцией называется процесс, при котором продуктом поглощаются из окружающей среды пары или газы. Процесс, обратный сорбции, называется десорбцией. Так как при сорбции и десорбции паров и газов происходит изменение качественных показателей пищевых продуктов, то необходимо устанавливать количество поглощаемых газов различными продуктами в зависимости от условий хранения, а также влияние поглощенного вещества на свойства того или иного продукта.
Увлажнение продукта происходит в том случае, если давление водяных паров в воздухе превышает давление водяных паров на поверхности продукта в результате испарения части из него свободной влаги.
Десорбция влаги продуктом происходит в том случае, когда давление водяных паров на поверхности продукта будет превосходить давление водяных паров в воздухе. Процессы сорбции или десорбции влаги продуктом идут до приобретения им равновесной влажности, когда давление водяного пара в воздухе и на поверхности продукта становится равным. В пористых телах полимолекулярная адсорбция осложняется капиллярной конденсацией. Вид изотерм сорбции зависит от радиуса пор  и давления или влажности воздуха. При этом сорбционная и десорбционная ветви изотермы не совпадают (Рис.6 6).
и давления или влажности воздуха. При этом сорбционная и десорбционная ветви изотермы не совпадают (Рис.6 6).
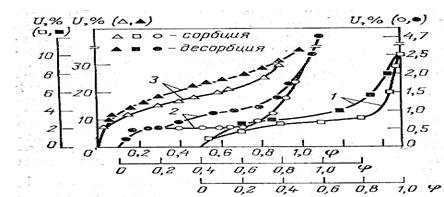
Рис. 6.6. Кривые сорбции и десорбции материала трех видов материалов
Поскольку в процессе сушки влажный материал стремится к фазовому равновесию, при котором наблюдается равенство химических потенциалов, то при достижении такого равновесия процесс сушки прекращается. Отсюда следует, что сушка относится к неравновесным процессам, обусловленным разностью химических потенциалов.
Многие процессы переноса описываются градиентным линейным законом (законы Фурье, Фика, Ньютона для жидкостей), гласящим, что плотность потока переноса  пропорциональна градиенту потенциала
пропорциональна градиенту потенциала  , т.е.
, т.е. 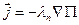 . Знак минус указывает на то, что плотность потока потенциала направлена в сторону убывания этого потенциала. Для процесса сушки можно записать
. Знак минус указывает на то, что плотность потока потенциала направлена в сторону убывания этого потенциала. Для процесса сушки можно записать  , где
, где 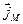 - плотность потока массы.
- плотность потока массы.
|
|
|
Закономерности сушки влажных материалов обуславливаются одновременным протеканием переноса теплоты и массы [24]:
- теплообмен между поверхностью материала и окружающей средой;
- испарение влаги с поверхности материала в окружающую среду (массоотдача);
- перемещение теплоты внутри материала (теплоперенос);
- перемещение влаги внутри материала (массоперенос).
При влажности высушиваемых материалов более 30% поверхность тела покрыта сплошной пленкой влаги. Влагой заполнены все микрокапилляры  и большинство макрокапилляров
и большинство макрокапилляров  . Влага испаряется с поверхности пленки, перемещается через пограничный слой к окружающей газовой среде под действием диффузии и отводится от поверхности тела в результате конвективной диффузии. Основное сопротивление на пути массопереноса влаги от пленки к среде оказывает ламинарный пограничный слой. Скорость диффузии газа через этот слой определяет интенсивность испарения влаги с поверхности тела.
. Влага испаряется с поверхности пленки, перемещается через пограничный слой к окружающей газовой среде под действием диффузии и отводится от поверхности тела в результате конвективной диффузии. Основное сопротивление на пути массопереноса влаги от пленки к среде оказывает ламинарный пограничный слой. Скорость диффузии газа через этот слой определяет интенсивность испарения влаги с поверхности тела.
При влажности материала больше гигроскопической пар, образующийся у поверхности, является насыщенным, а температура поверхности тела в случае конвективной сушки равна температуре мокрого термометра. Скорость сушки остается примерно постоянной. После исчезновения сплошной пленки влага начинает испаряться с концевых участков капилляров. Интенсивность сушки при этом увеличивается. При достижении материалом влажности меньше гигроскопической интенсивность сушки резко падает, а температура поверхности тела постепенно увеличивается. Поверхность испарения начинает перемещаться вглубь тела.
Тепло для испарения влаги передается от теплоносителя к поверхности тела и затем в результате теплопроводности проникает вглубь. Количественным показателем, характеризующим перенос влаги и тепла, являются числа Био:
-  - для массообмена;
- для массообмена;
-  - для теплообмена.
- для теплообмена.
При больших значениях числа 
 условия массообмена определяются в основном свойствами материала, а влияние внешних факторов на процесс сушки незначительно. К таким материалам относятся материалы с ультрамикропорами, влага в которых перемещается в результате твердотельной диффузии, поэтому коэффициенты диффузии очень малы и составляют от
условия массообмена определяются в основном свойствами материала, а влияние внешних факторов на процесс сушки незначительно. К таким материалам относятся материалы с ультрамикропорами, влага в которых перемещается в результате твердотельной диффузии, поэтому коэффициенты диффузии очень малы и составляют от  до
до 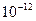 м2/с. С уменьшением числа
м2/с. С уменьшением числа 
 скорость сушки не зависит внутридиффузионного сопротивления материала, что позволяет интенсифицировать процесс сушки организацией соответствующей гидродинамической обстановки в аппарате. К таким материалам относятся сыпучие микропористые материалы со свободной или слабосвязанной влагой.
скорость сушки не зависит внутридиффузионного сопротивления материала, что позволяет интенсифицировать процесс сушки организацией соответствующей гидродинамической обстановки в аппарате. К таким материалам относятся сыпучие микропористые материалы со свободной или слабосвязанной влагой.
|
|
|
Блок-схема сушильной установки приведена на рис. 6.77

Рис. 6.6 Блок-схема сушильной установки
1 – воздухоподогреватель, 2 – сушильная камера
Здесь  - параметры воздуха на входе в подогреватель - влагосодержание, температура, энтальпия и относительная влажность соответственно,
- параметры воздуха на входе в подогреватель - влагосодержание, температура, энтальпия и относительная влажность соответственно,  - параметры воздуха на входе в сушильную камеру;
- параметры воздуха на входе в сушильную камеру;  - то же на выходе из сушильной камеры;
- то же на выходе из сушильной камеры;  - количество влаги в продукте. Расход тепла на 1 кг испаренной влаги
- количество влаги в продукте. Расход тепла на 1 кг испаренной влаги 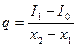 .
.
Расчет сушильных аппаратов при сушке материалов с известными свойствами основывается на составлении материального и теплового баланса и на условии, что время сушки, определяемое кинетикой процесса, не должно превышать фактическое время сушки, определяемое гидродинамикой аппарата.
Уравнение материального баланса можно составить для всех материальных потоков, проходящих через сушилку:
- по сухому материалу  ;
;
- по испаряемой влаге  ;
;
- по сушильному агенту  .
.
Например,  , где
, где  - конечное и начальное влагосодержание материала соответственно, или
- конечное и начальное влагосодержание материала соответственно, или 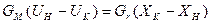 , где
, где 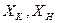 - конечное и начальное влагосодержание сушильного агента соответственно.
- конечное и начальное влагосодержание сушильного агента соответственно.
Тепловой баланс (рис. 6.8) для сушильной камеры записывается в виде 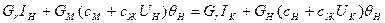 , где
, где  - начальная и конечная энтальпия сушильного агента;
- начальная и конечная энтальпия сушильного агента;  - начальная и конечная температура материала;
- начальная и конечная температура материала;  - теплоемкость материала и жидкости. При составлении теплового баланса принимают допущение, что процесс сушки близок к процессу при постоянном давлении, это позволяет считать, что количество тепла равно количеству энтальпии.
- теплоемкость материала и жидкости. При составлении теплового баланса принимают допущение, что процесс сушки близок к процессу при постоянном давлении, это позволяет считать, что количество тепла равно количеству энтальпии.
|
|
|
При тепловых расчетах реальных сушильных аппаратов учитываются потери тепла на перегрев образующегося пара, нагрев материала и транспортирующих элементов сушилки, потери в окружающую среду.

Рис. 6.8.Тепловой баланс сушилки
Перенос тепла в неподвижной среде и в пограничном слое обусловлен молекулярной теплопроводностью. Плотность потока тепла в соответствии с законом Фурье равна  , где
, где 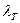 - молекулярная теплопроводность среды;
- молекулярная теплопроводность среды;  - температурный градиент. При конвективном переносе тепла плотность потока выразится как
- температурный градиент. При конвективном переносе тепла плотность потока выразится как  , где
, где  - соответственно скорость, плотность и теплоемкость газового потока.
- соответственно скорость, плотность и теплоемкость газового потока.
В пограничном слое доминирует молекулярный перенос, в глубине поверхности преобладает турбулентный и конвективный. Диффузионный и конвективный перенос тепла описывается уравнением конвективной теплопроводности [28]  , где
, где  - суммарная температуропроводность, обусловленная молекулярным и молярным переносом тепла.
- суммарная температуропроводность, обусловленная молекулярным и молярным переносом тепла.
Уравнение конвективной диффузии для пара имеет аналогичный вид  , где
, где  - суммарный коэффициент диффузии, обусловленный молекулярным и молярным переносом вещества;
- суммарный коэффициент диффузии, обусловленный молекулярным и молярным переносом вещества;  - концентрация влаги.
- концентрация влаги.
Процесс сушки при активных гидродинамических режимах характеризуется значительным числом параметров, изменяющихся по нелинейным законам, поэтому исследование закономерностей процесса целесообразно проводить на моделях. Структура модели определяется гидродинамическими параметрами и проявляется в характере распределения времени пребывания материала в аппарате. В зависимости от группы материала, как объекта сушки проводят моделирование гидродинамики, когда математическая модель совпадает с гидродинамической, или добавляют уравнение кинетики сушки, а в некоторых случаях и теплообмена.
При моделировании гидродинамики возможны два подхода: первый заключается в описании движения потока частиц материала с учетом их взаимодействия, второй – в аппроксимации типовыми моделями. Второй подход включает:
- выбор структуры потока;
- составление балансового уравнения относительно концентраций вещества в потоке;
- экспериментальная проверка параметров гидродинамической модели.
Распределение времени пребывания частиц материала в аппарате подчиняется статистическим законам распределения и находится по виду сигнала, проходящего через систему. Таким сигналом является подача индикатора на вход в виде импульса возмущения. В зависимости от вида функции распределения все многообразие моделей потоков, вне зависимости от типа сушилки можно представить в виде типовых моделей:
|
|
|
- идеального вытеснения,
- идеального смешения,
- диффузионной,
- ячеечной,
- комбинированной.
Для решения дифференциальных уравнений, описывающих гидродинамику, удобно использовать преобразование Лапласа [33]. Имея гидродинамическую модель аппарата можно получить функцию распределения по времени пребывания частиц в аппарате.
Известны дифференциальные и интегральные функции распределения, которым соответствуют  - кривые и
- кривые и  - кривые отклика на импульсное возмущение на входе в систему.
- кривые отклика на импульсное возмущение на входе в систему.
Пусть:
 - интегральная функция распределения, т.е. доля частиц, находящихся в аппарате в течение времени
- интегральная функция распределения, т.е. доля частиц, находящихся в аппарате в течение времени  или меньше
или меньше  ;
;
 - дифференциальная функция распределения, т.е. доля частиц, время пребывания которых в аппарате находится в интервале времени от
- дифференциальная функция распределения, т.е. доля частиц, время пребывания которых в аппарате находится в интервале времени от  до
до  .
.
Входным параметром является концентрация вещества на входе в аппарат  , выходным – концентрация на выходе
, выходным – концентрация на выходе  .
.
Если  , где
, где 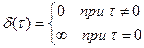 , то
, то  - функция веса.
- функция веса.
Если  - единичная функция, где
- единичная функция, где  , то
, то 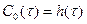 - переходная функция.
- переходная функция.
Если на входе в аппарат концентрация есть дельта-функция, то на выходе из аппарата концентрация равна дифференциальной функции распределения частиц по времени их пребывания в аппарате и зависимость  называется
называется  - кривой.
- кривой.
Если на входе в аппарат концентрация есть единичная функция, то на выходе концентрация равна интегральной функции распределения частиц во времени пребывания и зависимость  называется
называется  - кривой.
- кривой.
Передаточной функцией модели называется отношение преобразованного по Лапласу выхода к входу  . По передаточной функции можно написать дифференциальное уравнение модели и найти
. По передаточной функции можно написать дифференциальное уравнение модели и найти  . Кривая распределения
. Кривая распределения  характеризуется моментами. Обычно ограничиваются рассмотрением первого начального момента, соответствующего среднему времени пребывания материала в аппарате и второго центрального момента, соответствующего дисперсии распределения времени пребывания.
характеризуется моментами. Обычно ограничиваются рассмотрением первого начального момента, соответствующего среднему времени пребывания материала в аппарате и второго центрального момента, соответствующего дисперсии распределения времени пребывания.
Рассмотрим некоторые модели.
Модель идеального смешения. Сущность этой модели в том, что концентрация одинакова в любых точках аппарата. Модель описывается уравнением  , где
, где  - концентрация на входе и на выходе соответственно,
- концентрация на входе и на выходе соответственно,  - объемный расход потока, м3/с;
- объемный расход потока, м3/с;  - объем зоны идеального смешения, м3.
- объем зоны идеального смешения, м3.
Преобразование по Лапласу данного уравнения представляется следующим выражением 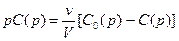 , отсюда передаточная функция
, отсюда передаточная функция 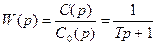 , где
, где  . Если
. Если  , то функция концентрации будет равна
, то функция концентрации будет равна  .
.
Ячеечная модель. Модель содержит  последовательно соединенных ячеек. Передаточная функция
последовательно соединенных ячеек. Передаточная функция  -ой ячейки
-ой ячейки  ,
,  .
.
Для одинаковых ячеек  , где
, где  .
.
Если  , то переходя от изображения к оригиналу, получим
, то переходя от изображения к оригиналу, получим  .
.
Модель идеального вытеснения. Согласно данной модели все частицы движутся с одинаковой скоростью. Уравнение модели идеального вытеснения выглядит следующим образом  , где
, где  скорость потока, м/с;
скорость потока, м/с;  - координата. В этом случае
- координата. В этом случае  .
.
Передаточная функция модели идеального вытеснения  , где
, где 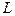 - размер аппарата, м;
- размер аппарата, м;  - время запаздывания, с. Любой сигнал на входе через время, равное
- время запаздывания, с. Любой сигнал на входе через время, равное 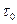 точно повторяется на выходе.
точно повторяется на выходе.
Однопараметрическая диффузионная модель. Согласно этой модели в объеме существуют два потока: основной, движущийся со скоростью  , и диффузионный поток
, и диффузионный поток 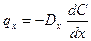 , где
, где  - количество вещества, проходящего через единицу поверхности в единицу времени, кг/(м2 ∙с);
- количество вещества, проходящего через единицу поверхности в единицу времени, кг/(м2 ∙с);  - коэффициент диффузии вдоль оси
- коэффициент диффузии вдоль оси  . Дифференциальное уравнение данной модели
. Дифференциальное уравнение данной модели  .
.
Для составления гидродинамических моделей используют массовые расходы, массовые концентрации, массу вещества в аппарате. Например, ячеечная модель может быть записана как  , где
, где 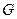 - массовый расход потока через аппарат, кг/с;
- массовый расход потока через аппарат, кг/с;  - масса
- масса  -й ячейки;
-й ячейки;  - массовая концентрация вещества в потоке, кг/кг.
- массовая концентрация вещества в потоке, кг/кг.
Неизвестные параметры модели определяют исходя из кривых отклика с использованием метода моментов, метода наименьших квадратов и др.
|
|
|


