Перенос теплоты и массы вещества в коллоидных капиллярно - пористых телах

 

Многие процессы пищевых производств, протекающие в технологическом оборудовании и связанные с тепловой обработкой материалов, сопровождаются одновременно процессами переноса массы вещества и теплообмена.

Влага, имеющая физико-механическую связь, удерживается в капиллярах и в зависимости от режима нагревания может перемещаться в виде жидкости или в виде пара. Внутри влажного материала влага перемещается в направлении потока теплоты. Это создает в высушиваемом материале градиент влагосодержания.

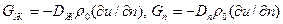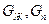Плотность потока жидкости и пара, проходящих через единицу поверхности, перпендикулярной направлению перемещения, в единицу времени, пропорционально градиенту влагосодержания коллоидного капиллярно-пористого тела равна , где - плотность потока жидкости и пара соответственно, кг/(м²∙с); 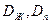- коэффициенты диффузии для жидкости и пара соответственно; 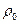- плотность абсолютно сухого материала, 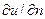- градиент влагосодержания. Знак минус указывает, что в направлении нормали влагосодержание уменьшается.

Общий поток влаги 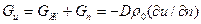, где 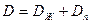. Данное соотношение является основным законом перемещения влаги в коллоидном капиллярно-пористом теле, как в виде пара, так и в виде жидкости при наличии градиента влагосодержания.

Коэффициент диффузии 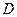включает четыре слагаемых, характеризующих перемещение определенного вида влаги , где:

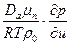- коэффициент диффузии, характеризующий перемещение адсорбционной влаги; 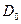- коэффициент диффузии, характеризующий перемещение осмотической влаги; 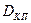- коэффициент диффузии, характеризующий перемещение капиллярной влаги в виде пара; - коэффициент диффузии, характеризующий перемещение капиллярной влаги в виде жидкости. Здесь 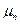- молекулярная масса пара, 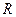- универсальная газовая постоянная, 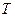- абсолютная температура, 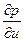- учитывает зависимость между давлением пара коллоидного тела и его влагосодержанием .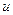

При наличии в коллоидном капиллярно-пористом теле перепада температур будет наблюдаться поток влаги, обусловленный температурным градиентом, плотность потока которого пропорциональна этому градиенту 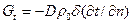, где 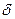- термоградиентный коэффициент, 1/град; 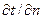- градиент температуры, град/м. Данное уравнение является выражением закона термовлагопроводности.

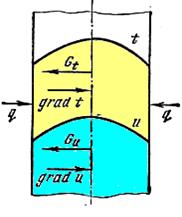
При наличии внутри влажного материала градиента влагосодержания и градиента температуры влага начнет перемещаться вследствие влагопроводности и термовлагопроводности. Например, при контактной сушке направления градиентов совпадают, поэтому термовлагопроводность усиливает общую влагопроводность и процесс сушки ускоряется (рис. 6.1)

Рис. 6.1 Схема направления градиентов температуры и влагосодержания при контактной сушке продукта

Из-за отдачи теплоты в окружающую среду поверхностные слои продукта охлаждаются и температура на поверхности становится ниже, чем внутри. Это распределение температуры вызывает температурный градиент, направленный от поверхности продукта к его середине и увеличивающий общую влагопроводность.

Общий поток влаги равен сумме потоков 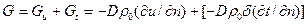- уравнение обобщенного закона перемещения влаги в коллоидных капиллярно-пористых телах.

При противоположных направлениях градиента влагосодержания и градиента температуры направление суммарного потока влаги зависит от соотношения сил влагопроводности 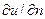и термовлагопроводности .

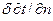Например, при конвективной сушке вследствие прогрева материала с поверхности и испарения влаги внутри высушиваемого материала возникнет градиент влагосодержания 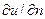, направленный от поверхности к середине материала, а вследствие термовлагопроводности – градиент термовлагосодержания 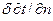, направленный от середины к поверхности материала (рис.6.2). В результате возникнут два противоположных направления потока влаги – за счет влагопроводности 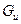к поверхности, и за счет термовлагопроводности 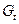- к середине.

Рис.6.2 Схема направлений градиентов влагосодержания и температуры при конвективной сушке материала

Суммарный поток влаги равен .

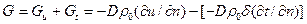При большей интенсивности влагопроводности по сравнению с термовлагопроводностью влага будет перемещаться от внутренних слоев материала к поверхностным, и термовлагопроводность будет препятствовать перемещению потока влаги.

При большей интенсивности термовлагопроводности влага будет перемещаться по направлению потока теплоты, т.е. в направлении увеличения влагосодержания – от поверхности материала вглубь, а влагопроводность будет снижать поток влаги. Например, данное явление наблюдается при инфракрасной сушке и в процессе выпечки хлебобулочных изделий: перемещение влаги в направлении потока теплоты постепенно увеличивает градиент влажности, отчего влагопроводность растет. Через некоторое время возникнет равенство, т.е. термовлагопроводность будет полностью уравновешена влагопроводностью. В этот момент влажность в центральных слоях продукта остается постоянной, а высушивание происходит за счет углубления зоны испарения

Поток влаги от термовлагопроводности будет переносить с собой и дополнительную теплоту в направлении основного теплового потока, поэтому основной закон теплопроводности для случая нагревания влажных материалов выражается уравнением 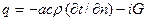, где 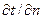- градиент температуры, 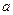- коэффициент температуропроводности, 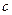- удельная теплоемкость, - плотность материала продукта, 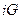- количество теплоты, переносимое влагой, - энтальпия жидкости, 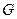- плотность потока влаги.

Из основного закона перемещения влаги и закона теплопроводности для влажных материалов получают систему уравнений, моделирующих перемещение теплоты и влаги во влажных материалах.

Дифференциальное уравнение переноса вещества выводится из основного уравнения переноса с использование закона сохранения массы к некоторому произвольно взятому объему, ограниченному замкнутой поверхностью.

С учетом зависимости от температуры и влажности коэффициентов диффузии 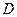, теплопроводности 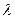, термоградиентного коэффициента 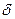получают систему нелинейных дифференциальных уравнений в частных производных. При допущении постоянства этих коэффициентов, используя закон переноса жидкости и преобразование Остроградского-Гаусса, можно получить дифференциальное уравнение переноса в следующем виде 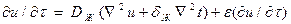, где - коэффициент, характеризующий долю влаги, перемещающейся в виде пара (критерий внутреннего испарения или фазового превращения). При отсутствии внутреннего испарения (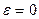) влага перемещается в виде жидкости, при 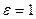изменение влагосодержания в продукте происходит только за счет испарения жидкости и конденсации пара при отсутствии переноса жидкости.

Дифференциальное уравнение переноса пара при 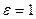имеет вид .

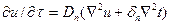Для зональной системы расчета тепломассопереноса дифференциальные уравнения переноса имеют вид

,

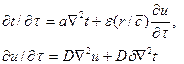где 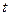- температура тела, 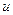- удельное влагосодержание, 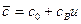- удельная теплоемкость влажного материала, 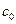- удельная теплоемкость сухого материала, 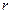- удельная теплота испарения, 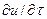- изменение влагосодержания в элементарном объеме в единицу времени вследствие испарения или конденсации внутри материала, 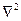- оператор Лапласа.

Эти два уравнения полностью описывают внутренний тепло- и массоперенос и их решение при условии постоянства массообменных характеристик позволят теоретически рассчитать поля температуры и влагосодержания влажного материала. Значения 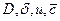определяются экспериментально.

Аналитическое решение данных уравнений для коллоидных капиллярно-пористых тел не всегда возможно. Однако при наличии условий однозначности можно получить числа и уравнения подобия, с помощью которых определить числовые характеристики процесса переноса.

Из дифференциальных уравнений и граничных условий, характеризующих балансы влаги и теплоты, выводится ряд чисел подобия, например:

- число Фурье 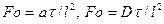, характеризующее гомохронность полей переноса теплоты и массы вещества;

- число Лыкова , характеризующее инерционность поля влажности по отношению к инерционности температурного поля;

- число Поснова , характеризующее относительный перепад удельного влагосодержания к перепаду температуры;

- число Нуссельта 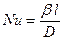, характеризующее интенсивность массоотдачи. Здесь величина является толщиной пограничного слоя жидкости;

- диффузионный критерий Пекле, являющийся мерой отношения количества вещества, перенесенного конвекцией, к количеству вещества, перенесенному молекулярной диффузией ;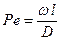

- диффузионный критерий Прандтля, характеризующий связь концентрационных и скоростных полей в потоке, 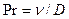, и др.

Коэффициенты тепло - и массопереноса при испарении жидкости со свободной поверхности в условиях естественной конвекции рассчитываются по формулам, полученным Нестеренко А.В.:

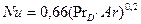при ,

при .

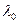В этих уравнениях коэффициент теплопроводности подсчитывается по формуле , где - коэффициент теплопроводности сухого газа, 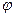- влажность газа.

При определении потоков теплоты и массы при внешнем тепло- и массообмене необходимо определять температуру поверхности, которая отлична от температуры в глубине жидкости, за исключением адиабатного процесса. Для неадиабатных условий температура поверхности с достаточным приближением равна:

- для условий свободной конвекции ,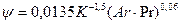

- для условий вынужденной конвекции ,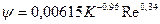

где 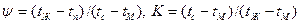, 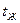- температура в толще воды, 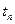- температура поверхности воды, - температура воздуха по мокрому термометру.

Уравнения подобия процессов тепло- и массообмена при испарении жидкости с поверхности капиллярно-пористого тела:

- для теплообмена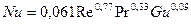

- для массообмена .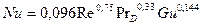

Интенсивность тепло- и массопереноса прямо пропорциональна температуре, скорости движения потока и обратно пропорциональна влажности паровоздушной среды.

Механизм переноса теплоты и влаги при испарении из влажного материала (процесс сушки) отличается от механизма переноса при испарении со свободной поверхности жидкости. Процесс сушки происходит при непрерывном углублении поверхности испарения и при постоянном увеличении толщины зоны испарения. При углублении поверхности испарения температура внутри материала ниже, чем на его внешней поверхности, в результате чего в зоне испарения создается температурный напор. С увеличением температурного напора по вектору потока теплоты (от поверхности внутрь тела) увеличивается коэффициент теплоотдачи. При углублении поверхности испарения коэффициент теплоотдачи больше чем при испарении с внешней поверхности.

При испарении влаги из высушиваемого материала с углублением поверхности испарения перенос пара идет через зону испарения. В микропорах молекулы пара и воздуха движутся независимо, т.е. перенос пара происходит эффузией.

Плотность эффузионного потока 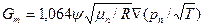, где 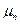- молекулярная масса пара, 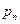- парциальное давление пара, 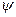- коэффициент молекулярного течения, пропорциональный среднему радиусу капилляра.

Плотность диффузионного потока вещества 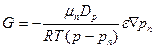, где 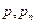- барометрическое и парциальное давления пара соответственно, - коэффициент пористости материала, - оператор Гамильтона.

Потенциалом диффузионного переноса является 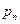, потенциалом эффузионного - 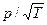. При капиллярах радиусом более 10^-5 см через зону испарения осуществляется смешанный диффузионно-эффузионный перенос.

Поскольку температура поверхности испарения меньше температуры на внешней поверхности материала, то в зоне испарения возникает градиент эффузионного переноса, что способствует интенсивному переносу пара через зону испарения.

Диффузионный перенос в микрокапиллярах осложняется явлением теплового скольжения. При значительной длине капилляра возникает перепад температуры и появляется циркуляция воздуха, направленная у стенок капилляра против потока теплоты, а по оси – по направлению потока. Поскольку у поверхности испарения внутри материала температура меньше, чем у внешней поверхности, то возникает движение газа к поверхности материала. Тепловое скольжение усиливает перенос пара через зону испарения.

Перенос теплоты и вещества с поверхности материала в окружающую среду осуществляется теплопроводностью и диффузией. При этом интенсивный эффузионный перенос пара в зоне испарения и тепловое скольжение создают градиент давления в данной зоне, что изменяет механизм переноса пара в пограничном слое. Пар на выходе из зоны испарения турбулизирует пограничный слой воздуха около поверхности материала, в результате чего повышается интенсивность массообмена.

Т.о., тепло - и массообмен между поверхностью влажного материала при его высушивании и окружающей средой рассматривается в виде сочетания тепло- и массопереноса в зоне испарения внутри материала и в пограничном слое воздуха.

Основными коэффициентами переноса являются коэффициенты теплопроводности, диффузии, температуропроводности и термовлагопроводности.

В сухом состоянии теплообмен происходит без массообмена и рассчитанные коэффициенты теплопроводности практически совпадают с действительными.

В сухом капиллярно-пористом теле передача теплоты осуществляется теплопроводностью через твердый скелет тела и конвекцией и излучением между стенками пор. Эти виды теплопереноса определяются эквивалентным коэффициентом теплопроводности 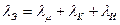. Плотность теплового потока в этом случае равна 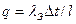, где - размер поры, 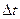- перепад температуры в порах тела.

Во влажных телах теплообмен всегда сопровождается массообменом. При этом возникает градиент переноса вещества, зависящий от температуры, поэтому экспериментальные значения коэффициента теплопроводности соответствуют эквивалентным, а не истинным значениям. Разница равна дополнительному потоку теплоты, вызванному переносом вещества и отнесенному к единичному градиенту температуры (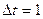), т.е. .

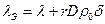Коэффициент температуропроводности равен , где 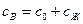- удельная теплоемкость влажного тела.

 

⇐ Предыдущая16171819202122232425Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: