Методы и задачи оптимизации процессов

Сущность математического описания процесса, технической системы или отдельного объекта заключается в получении математической модели связывающей входные факторы и выходные параметры, например, характеристики сырья и выходящего продукта, , где - оператор, характеризующий математическую операцию преобразования входных функций в выходные функции .

Оптимальность процесса означает минимизацию или максимизацию значений некоторой функции, адекватно описывающей данный процесс. Нахождение экстремума функции является классической задачей математического анализа, когда переменные могут изменяться во всем пространстве без каких-либо ограничений. Если функция непрерывно дифференцируема, то экстремальные значения будут в точках, в которых обращаются в нуль все частные производные функции.

Отыскание оптимума функции относится к задачам выпуклого программирования.

Функция , определенная на выпуклом множестве -мерного пространства, называется выпуклой на этом множестве, если для любых точек и любого числа (рис. 7.1)

Рис. 7.1.График функции одной переменной, выпуклой на всей числовой прямой

Рассмотрим постановку задачи выпуклого программирования. Пусть задана система ограничений какого-либо процесса (например, по скоростному режиму рабочих органов, по температурно-влажностным условиям и т.п.) и функция .

Задача выпуклого программирования состоит в отыскании такого решения системы ограничений, при котором целевая функция достигнет экстремального (минимального для выпуклой и максимального для вогнутой функции) значения. Если целевая функция является строго выпуклой (строго вогнутой) и если область решений системы ограничений не пуста и ограничена, то задача выпуклого программирования всегда имеет единственное решение [38].

Пример: Требуется найти минимум функции при следующих ограничениях: .

Построим область допустимых решений данной задачи:

- первое неравенство представляет собой окружность с центром в начале координат и радиусом . Очевидно, область решений данного неравенства лежит внутри окружности и на ней самой;

- область решений неравенства представляет собой полуплоскость, лежащей над этой прямой, включая и саму прямую;

- область решений неравенства представляет собой полуплоскость, лежащей под этой прямой, включая и саму прямую;

Можно видеть, что с учетом не отрицательности переменных областью допустимых решений данной задачи является замкнутый сектор, ограниченный прямыми и начальной окружностью (Рис. 7.2).

Построим линию уровня функции и определим направление ее убывания. Все линии уровня имеют уравнение , т.е. . При получаем линию уровня , представляющую собой окружность с центром в точке и радиусом .

Можно видеть, что в любой точке этой линии уровня при перемещении от центра окружности функция , а при перемещении к центру – убывает. Минимум достигается в точке , т.е. .

Рис. 7.2. Отыскание минимума функции

Для приближенного решения задач выпуклого программирования может быть использован метод кусочно-линейной аппроксимации. Идея метода состоит в том, что все из , где - целевая функция, и все (ограничения) заменяются ломаными линиями из прямолинейных отрезков.. При этом исходная задача выпуклого программирования заменяется новой задачей линейного программирования. Новая задача обычно решается симплексным методом.

Из градиентных методов в исследованиях процессов используется метод спуска. Общая схема решения задач этим методом состоит в построении последовательности 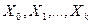решений системы ограничений данной задачи по следующему правилу: в качестве выбирается произвольная точка области решений, затем каждая последующая точка получается из предыдущей по формуле , где - некоторое направление (вектор), 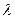- число (длина вектора). Направление и величина 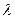выбираются так, чтобы обеспечить сходимость последовательности к оптимальному решению . Определить является ли направление приемлемым для продвижения к оптимуму можно по производной по направлению , если производная меньше нуля, то по данному направлению мы приближаемся к оптимуму.

Подробные сведения о методах оптимизации приведены в [39,40,41].