Оптимизация состава сыпучих смесей

При исследовании влияния на свойства продукта основных компонентов смеси задача получения модели при 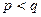сводится к известному факторному планированию эксперимента.

Если требуется получение регрессионной модели, когда одновременно варьируются доли всех компонентов смеси, матрицу эксперимента видоизменяют для выполнения условия, .

Геометрическое место точек, удовлетворяющее данному условию, представляет собой 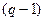- мерный правильный симплекс (при = 3 это треугольник, при = 4 – тетраэдр).

Каждой точке симплекса соответствует смесь определенного состава, наоборот, любому набору долей компонентов соответствует определенная точка симплекса.

При построении диаграмм «состав-свойство» исследуется факторное пространство в виде симплексов, поэтому координаты компонентов определяют не в обычной системе координат, а в симплексной системе, в которой доли каждого компонента откладываются вдоль ребер симплекса (рис. 7.3).

Перемещению точки вдоль оси 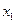от центра координат, в которой содержание компонента 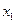равно нулю, к точке 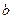, где доля 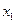= 1, соответствует перемещению точки вдоль ребра симплекса от точки 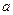, где 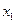= 0, к точк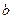е , где 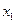= 1. Аналогично определяется содержание компонентов и .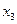

 

 

Рис. 7.3 Схема расположения точек на симплексе трехкомпонентной смеси

а – модель второго порядка, б – неполный полином третьей степени, в – полином третьей степени, г – неполный полином четвертой степени

 

Для определения долевого участия компонентов, соответствующих какой-либо точке смеси, достаточно провести через эту точку прямую параллельную ребру 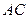и взять отрезок, соответствующий содержанию в смеси компонента , затем провести через эту же точку прямую параллельную , и взять отрезок, соответствующий доле 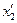. Далее провести прямую, параллельную и соответствующий отрезок покажет содержание в смеси компонента 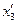(рис. 7.4).

Из рисунка 7.4 можно видеть, что вершины правильного симплекса соответствуют чистым компонентам, а остальные экспериментальные точки равномерно распределены внутри симплекса и на его ребрах.

 

 

 

Рис. 7.4 Схема перехода от прямоугольной системы (а) к симплексной системе координат (б)

 

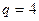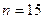Общее число экспериментальных точек симплексной решетки в зависимости от компонентов и степени полинома равно . Например, для полинома второй степени при при и при 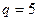, для полинома третьей степени соответственно равно 7; 14; 25.

Поскольку при условии 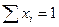доля одного из компонентов смеси однозначно определяется через доли всех остальных компонентов, т.е. не может изменяться независимо, то для описания взаимосвязи «состав-свойство» вместо полных полиномов вида 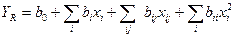используются так называемые приведенные (канонические) полиномы, вид которых зависит от числа компонентов смеси и степени полинома. Так, для случая трех компонентов приведенный полином имеет вид

и коэффициенты регрессии равны.

Матрица данной модели имеет вид (табл.7.1)

Таблица 7.1

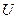
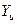
	½ ½	½ 1/2	½ 1/2	Y1 Y2 Y3 Y12 Y13 Y23

 

Расположение точек на симплексе трехкомпонентной смеси для модели в виде полинома второго порядка приведено на рис. 7.3.

Для компонентной смеси 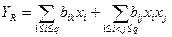, где .

Функция, зависящая от состава компонентной смеси и расположения точек в факторном пространстве, равна 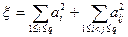, где .

Аналогично по соответствующим формулам определяются коэффициенты для полиномов других степеней и компонентных смесей.

Поскольку симплекс-решетчатые планы являются насыщенными, т.е. число опытов равно числу определяемых коэффициентов в полиноме, то степеней свободы для проверки адекватности модели не остается, поэтому для проверки адекватности проводятся дополнительные опыты в некоторых контрольных точках. Эти точки выбирают так, чтобы их можно было бы использовать при необходимости для построения полинома более высокой степени. Адекватность модели проверяется в каждой контрольной точке по 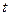-критерию

Расчетное значение 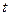- критерия равно , где 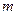- число опытов в контрольной точке, 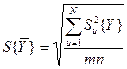- среднеквадратическая ошибка опыта. Расчетное значение критерия сравнивается с табличным. При гипотеза об адекватности модели не отвергается, 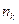.- число контрольных точек в симплексе.

Пример: Пусть требуется определить взаимосвязь между составом смеси и некоторым выходным параметром продукта, например, питательной ценностью и т.п. Для этого проводился активный эксперимент по симплекс-решетчатой матрице с участием трех компонентов. Матрица включает семь опытов, каждый из которых повторялся дважды.

Имеется: 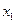- доля первого компонента, - доля второго компонента, 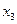- доля третьего компонента

Матрица планирования (табл. 7.2)

Таблица 7.2

№ опыта	Состав смеси	Выходной параметр	№ параметра
х1	х2	х3	Y1u	Y2u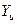
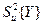
1 2 3 4 5 6 7 8 9	1 0 0 0,5 0,5 0 0,333 0,150 0,300	0 1 0 0,5 0 0,5 0,333 0,595 0,490	0 0 1 0 0,5 0,5 0,333 0,255 0,210	197,8 173,0 175,5 181,5 179,0 180,5 185,6 178,7 172,3	193,8 176,7 179,0 185,4 200,1 168,5 185,3 148,4 173,6	195,8 174,8 177,2 183,4 189,5 174,5 185,4 163,5 172,9	8,0 6,8 6,1 7,6 222,6 72,0 0,04 459,0 0,8	Y1 Y2 Y3 Y12 Y13 Y23 Y123=Y7 Y8 Y9

Значения коэффициентов полинома

Имеем .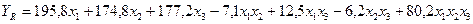

Подставив в полученную модель значения уровней факторов для опытов 7б 8 и 9, получим (табл. 7.3)

Таблица 7.3

U	YRu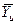
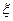
7 8 9	185,5 179,3 183,2	185,4 163,5 172,9	0,1 15,8 10,3	0,99 0,77 0,76	0,01 2,52 1,64

Однородность дисперсий для всех девяти опытов по критерию Кохрена 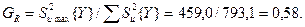Табличное значение критерия равно 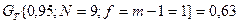. Поскольку 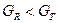, то дисперсии однородны.

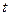Дисперсия воспроизводимости равна .Ошибка опытов . Расчетное значение -критерия 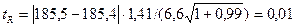. Табличное значение . Так как , то полученное уравнение адекватно опытным данным и может быть использовано для расчета выходного параметра продукта, получаемого из смеси компонентов.

На рис. 7.5 приведена диаграмма состояния «состав-свойство». На которой изображено семейство изолиний, показывающих характер изменения выходного параметра в зависимости от состава смеси. Можно видеть, что параметр увеличивается с увеличением доли первого и третьего компонента и с уменьшением второго. По данной диаграмме можно предсказать состав смеси, из которой можно выработать продукт с заданными свойствами.

Рис. 6.3 Диаграмма «Состав-свойство»

 

Для определения оптимального состава смеси по критерию стоимости и др. используются методы линейного или нелинейного программирования [39].

 

Условные обозначения

- целевая функция

- ограничения целевой функции

- направление (вектор) движения при поиске оптимума методом спуска

- число компонентов смеси

- дисперсия воспроизводимости

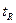- расчетное значение критерия Стьюдента

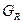- расчетное значение критерия Кохрена

 

Глоссарий

Выпуклая функция - функция , определенная на выпуклом множестве -мерного пространства, называется выпуклой на этом множестве, если для любых точек и любого числа

Метод кусочно-линейной аппроксимации - метод решения задач выпуклого программирования, суть которого состоит в том, что все из , где - целевая функция, и все (ограничения) заменяются ломаными линиями из прямолинейных отрезков.

Метод спуска – метод оптимизации, заключающийся в построении последовательности 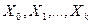решений системы ограничений, когда в качестве выбирается произвольная точка области решений, затем каждая последующая точка получается из предыдущей по формуле , где - некоторое направление (вектор), 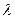- число (длина вектора).

Симплекс - геометрическое место точек, удовлетворяющее условию , представляющее собой в зависимости от числа параметров правильную геометрическую фигуру (при = 3 - треугольник, при = 4 – тетраэдр и т.д.).

 

Контрольные вопросы

1.Что означает понятие «оптимальность процесса»?

2.Какие функции относятся к выпуклым функциям?

3.В чем состоит задача выпуклого программирования?

4.В чем заключается сущность метода кусочно-линейной аппроксимации?

5.Какова общая схема поиска оптимума методом крутого спуска?

6.Что понимается под симплексом?

7.Каким образом определяют симплексным методом долевое участие компонентов в смеси?

8.Что изображается на диаграмме «состав-свойство», построенной симплексным методом?

 

Литература

1.Панфилов В.А. Технологические линии пищевых производств. – М: Колос,1993.

2.Авроров В.А., Жистин Е.А., Моряхина Н.В. Основы проведения научных исследований. В 2-х кн. – Пенза: ПГТА, 2009. 476с.

3.Вентцель Е.С. Элементы теории игр. – М: Физматгиз, 1969.

4.Кремер Н.Ш. Исследование операций в экономике. Учебное пособие. – М: ЮНИТИ, 2005.

5.Черчмен У. и др. Введение в исследование операций. – М: Наука, 1969.

6.Справочник металлиста. Под ред. Богуславского Б.Л. т.5, - М: Машиностроение, 1978. -673с.

7.Первозванский А.А. Математические модели в управлении производством. – М: Наука, 1975. – 615с.

8.Козлова О.В. Автоматизированная система управления. Т.1,2, - М: Мысль, 1972. - 454 с.

9.Пискунов Н.С. Дифференциальное и интегральное исчисления. В 2-х т. – М: Наука, 1976, -1312с.

10.Соколов А.Я. Основы расчета и конструирования машин и аппаратов пищевых производств. – М: Машиностроение, 1969. 639с.

11.Кретов И.Т. и др. Технологическое оборудование предприятий пищеконцентратной промышленности. – Воронеж: Изд. Воронеж. ун-та, 1996. -448с.

12.Аминов М.С. и др. Технологическое оборудование консервных заводов. – М: Пищ. пром-ть, 1986. -319с.

13.Лисовенко А.Т. Технологическое оборудование хлебозаводов и пути его совершенствования. – М: Легпищепром, 1982. – 208с.

14.Вайткус В.В. Гомогенизация молока. – М: Пищ. пром-ть, 1967. - 216c.

15.Андреев В.Г. и др. Лабораторный практикум по технологическому оборудованию пищевых производств. – М: МТИПП, 1990. -79с.

16. Гатилин Н.Ф. Проектирование хлебозаводов. – М: Пищ. пром-ть, 1975. 374с.

17.Остриков А.Н. и др. Практикум по курсу технологическое оборудование. – Воронеж, ВГТА, 1999. -424с.

18.Авроров В.А., Авроров Г.В., Сарафанкина Е.А. Моделирование операций обработки сырья и получения полуфабрикатов для мучных кондитерских изделий. Монография. – Пенза: ПГТА, 2010. -196с.

19. Валентас К.Дж., Ротштейн Э., Сингх Р.П. Пищевая инженерия. Справочник с примерами расчетов. – С.Пб: Профессия, 2004.

20.Азаров Б.М. и др. Технологическое оборудование пищевых производств. – М: Агропромиздат, 1988. – 463с.

21.Липатников В.Е., Казаков К.М. Физическая и коллоидная химия. – М: Высшая школа, 1975.- 200с.

22. Система научного инженерного обеспечения пищевых и перерабатывающих отраслей АПК России./А.Н.Богатырев и др. – М: Пищевая промышленность,. 1995.-528с.

23. Фейнман Р. И др. Фейнмановские лекции по физике. т.7. Физика сплошных сред. – М: Мир, 1977. -288с.

24. Сажин Б.С. Основы техники сушки. – М: Химия. -320с.

25.Барановский Н.В. и др. Пластинчатые и спиральные теплообменники. – М: Машиностроение, 1973.-288с.

26.Флауменбаум Б.Л. Теоретические основы стерилизации консервов. – Киев: Высшая школа, 1981. -196с.

27.Гребенюк С.Н. Технологическое оборудование сахарных заводов. – М: Легпищепром, 1983. -342с.

28.Лыков А.В. Теория теплопроводности. – М: Высшая школа, 1967. -599с.

29.Лебедев П.Д. теплообменные, сушильные и холодильные установки. – М: Энергия, 1972. -320с.

30.Курочкин А.А. и др. Машины и аппараты для переработки молока. – Пенза: ПГТА, 2008. – 295с.

31.Малкин А.Я., Исаев А.И. Реология: концепции, методы, приложения. – С-Пб: Профессия, 2007.

32.Новичихин В.А. Прикладная теория свободного движения тела. – Горький: Волго-Вятское кн. изд., 1973.

33.Г.Корн, Т.Корн. Справочник по математике для научных работников и инженеров. Изд. 5-е. – М: Наука, 1984. – 831с.

34.Федоренко Б.Н. Научное обеспечение процессов мембранного ферментов. Автореферат дисс. д.т.н. – М: 2002.

35.Фатыхов Ю.А., Канопка Л. Экструзионные технологии пищевых производств. – Вильнюс: Техника, 2007. – 88с.

36.Остриков А.Н. и др. Экструзия в пищевой технологии. – СПб: ГИОРД, 2004. – 288с.

37.Соколов А.Я. Прессы пищевых и кормовых производств. – М: Машиностроение, 1973. -288с.

38.Кремер Н.Ш. Исследование операций в экономике. – М: ЮНИТИ, 2005. -407с.

39.Акулич И.Л. Математическое программирование в примерах и задачах. – М: Высшая школа,1986.

40.Моудер Дж, Элмаграби С. Исследование операций. В 2-х кн. – М: Мир, 1981.

41.Кофман А. Методы и модели исследования операций. – М: Мир, 1966.

42.Стабников В.Н. и др. Процессы и аппараты пищевых производств. – М: 1966, -с.635.

43.Эберт Г. Краткий справочник по физике. – М: Физматгиз, 1963. -с. 552.

44.Авроров В.А. Устройство распределения волокнистых материалов по емкостям. Авт. св. №

 

 

⇐ Предыдущая19202122232425262728

Поделиться:

Воспользуйтесь поиском по сайту: