Расчетная работа 2: Применение математического ожидания и стандартного отклонения для целей оценки предпринимательского риска

 

Методические пояснения:

Математическое ожидание и стандартное отклонение наиболее часто на практике применяют в том случае, когда сравниваются варианты инвестирования, для которых известны возможные значения прибыли (х₁ … х_n) а также вероятности (р₁ … р_n) получения данной прибыли соответственно. Однако следует помнить, что реальное применение этого метода оценки рисков для предпринимательской деятельности гораздо шире. Главное в данном случае, чтоб по каждому из вариантов можно было определить сравниваемый параметр и вероятность проявления его конкретного значения.

Дня каждого варианта вычисляются математическое ожидание 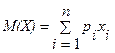, которое характеризует среднюю величину исхода рассматриваемого рискового события и стандартное отклонение 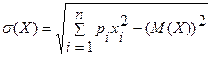, которое в данном случае является формализованным показателем оценки риска.

На практике при применении методов математического ожидания и стандартного отклонения следует помнить, что стандартное отклонение является мерой риска, многими воспринимается как аксиома. Но этот показатель не всегда точно отражает действительность. Ожидаемые доходы, как правило, оцениваются с помощью прошлых доходов. При значительном изменении со временем активов предприятия прогнозы, полученные на основании данных прошлых лет, будут совершенно бесполезными при оценке риска. Так же инвесторы при принятии решений ориентируются на ожидаемую доходность инвестиций. При хороших перспективах роста предприятия можно ожидать и высоких доходов. Но высокий доход связан с высоким риском. Поэтому следует обратить особое внимание на такие факторы, как общее состояние экономики, отрасль экономики и показатели конкретного предприятия.

Пример:

В таблице указаны вероятности получения прибыли для двух вариантов инвестирования. Сравним эти варианты:

 

	Распределение вероятности
Прибыль, млн. руб.	-2	-1
Вариант 1	0,1	0,1	0,3	0,2	0,3
Вариант 2	0,1	0,2	0,1	0,2	0,2	0,2

 

Заполним расчетную таблицу:

- числа из 1-й, 2-й и 3-й строк исходной таблицы запишем в 1-м, 2-м и 5-м столбцах новой таблицы соответственно;

- 3-й (6-й) столбец равен произведению 1-го и 2-го (5-го) столбцов;

- числа 3-го (6-го) столбца умножаем на числа 1-го столбца и результат пишем в 4-м (7-м) столбце;

- в последней строке указаны суммы элементов соответствующих столбцов.

 

Прибыль (x)	Вариант 1	Вариант 2
p	р×х	px2	p	р×х	px2
-2	0,1	-0,2	0,4	0,1	-0,2	0,4
-1	0,1	-0,1	0,1	0,2	-0,2	0,2
	0,3			0,1
	0,2	0,2	0,2	0,2	0,2	0,2
	0,3	0,6	1,2	0,2	0,4	0,8
				0,2	0,6	1,8
Сумма		0,5	1,9		0,8	3,4

 

Для 1-го варианта математическое ожидание М(Х) и стандартное отклонение σ(Х) равны:

М(Х) = 0,5;

σ(Х) = 1,28;

Для 2-го варианта математическое ожидание М(Х) и стандартное отклонение σ(Х) равны:

М(Х) = 0,8;

σ(Х) = 1,66;

Мы видим, что во 2-м варианте средняя ожидаемая прибыль выше, но и оценка риска во 2-м варианте больше. Инвестор, склонный к риску, предпочтет 2-й вариант. Более осторожный инвестор ограничится 1-м вариантом.

 

Задание для самостоятельного решения:

2.1. В таблице указаны вероятности получения прибыли для пяти вариантов инвестирования.

 

Условия для задания 2.1

	Распределение вероятности
Прибыль, млн. руб.	-2	-1
Вариант 1	0,4	0,2	0,1	0,2	0,1
Вариант 2	0,3	0,2	0,1	0,2	0,1	0,1
Вариант 3	0,4	0,2		0,1	0,2	0,1
Вариант 4		0,1	0,2	0,4	0,1	0,2
Вариант 5	0,1	0,2	0,1	0,3	0,2	0,1

 

Студентам необходимо провести сравнение предложенных вариантов инвестирования, используя показатели математического ожидания и стандартного отклонения. Результаты расчетов требуется представить графически и сопроводить их развернутыми выводами.

2.2. В таблице приведены вероятности производительности труда работников цеха. Применив показатели математического ожидания и стандартного отклонения студентам необходимо выявить наиболее работоспособного и «рискованного» работников.

 

Условия для задания 2.2

	Распределение вероятности
Выработка за смену (тыс. руб.)		0,5		1,5		2,5
Работник 1		0,12	0,35	0,28	0,15	0,07	0,03
Работник 2	0,02	0,31	0,23	0,21	0,17	0,06
Работник 3	0,01	0,27	0,26	0,19	0,11	0,08	0,08
Работник 4	0,01	0,14	0,07	0,33	0,23	0,16	0,06
Работник 5	0,02	0,25	0,19	0,15	0,21	0,17	0,01

 

По каждому из двух предложенных заданий от студентов требуется рассмотреть не менее двух вариантов для сравнения. По полученным результатам необходимо письменно сделать выводы и дать соответствующие пояснения.

 

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: