 |
Расчетная работа 3: Анализ результатов экспертных процедур в области оценки предпринимательских рисков
|
|
|
|
Методические пояснения:
По итогам проведения экспертной процедуры (опросов и анкетирования) целесообразно провести тестирование мнения группы экспертов и проверку их согласованности. Наиболее часто для этих целей используют коэффициент конкордации (от лат. concordare – привести в соответствие, упорядочить), величина которого позволяет судить о степени согласованности мнений экспертов и, как следствие, о достоверности их оценок.
Согласованность мнения экспертов можно оценивать по величине коэффициента конкордации Кендалла, который рассчитывается следующим образом:

где S – сумма квадратов отклонений всех оценок рангов каждого объекта экспертизы от среднего значения;
n – число экспертов;
m – число объектов экспертизы.
Средняя оценка результат экспертного мнения в данном случае рассчитывается по следующей формуле:
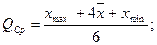
где xmax – максимальная оценка экспертов относительно объекта экспертизы;
xmin – минимальная оценка экспертов относительно объекта экспертизы;
 –средняя арифметическая оценки экспертов относительно объекта экспертизы.
–средняя арифметическая оценки экспертов относительно объекта экспертизы.
Так же коэффициент конкордации может быть определен по методу дисперсионных оценок мнений экспертов, для этого необходимо использовать следующее выражение:

где σ2ф – фактическая дисперсия суммарных (упорядоченных) оценок, данных экспертами;
σ2max – дисперсия суммарных (упорядоченных) оценок в случае, когда мнения экспертов полностью совпадают.
При этом дисперсия рассчитывается по стандартной модели:

В качестве x используется суммарная оценка объекта экспертизы, а среднее значение суммарной оценки экспертов здесь определяется следующим образом:
|
|
|

Коэффициент конкордации может изменяться в диапазоне 0 < W < 1, при этом если он равен 0, то наблюдается полная несогласованность экспертов, а если он равен 1, то считается, что эксперты проявили полное единодушие. В то случае если его значение находится в интервале 0 < W < 0,5, то результаты проведенного опроса рассматриваются как неудовлетворительные и их экспертную процедуру рекомендуется провести заново либо по иному блоку вопросов, либо с иным составом экспертов. При большом числе экспертов он может быть относительно выровнен путем исключения из результатов оценки мнений отдельных (обычно самых противоречивых) экспертов, но число таких исключений не должно превышать 5% от общего числа опрошенных экспертов.
Пример
Необходимо определить степень согласованности мнения четырех экспертов, чьи результаты ранжирования трех объектов экспертизы приведены в таблице.
| Номер объекта экспертизы | Оценка эксперта | Сумма рангов | Отклонение от среднего | Квадрат отклонения | W | |||
| 1-го | 2-го | 3-го | 4-го | |||||
| 0,50 | 0,75 | 0,50 | 0,75 | 2,50 | -0,45 | 0,2025 | 0,017 | |
| 0,25 | 0,50 | 0,75 | 0,75 | 2,25 | -0,20 | 0,04 | ||
| 0,50 | 0,25 | 0,25 | 0,50 | 1,50 | 0,55 | 0,3025 | ||
| Q = | 2,05 | S = | 0,545 |
1) рассчитаем сумму рангов по каждому объекту экспертизы:
1-ый: 0,5 + 0,75 +0,5 +0,75 = 2,50,
2-ой: 0,25 + 0,5 +0,75 + 0,75 = 2,25,
3-ий: 0,50 + 0,25 + 0,25 + 0,5 = 1,50;
2) определим среднюю оценку результата экспертного мнения:
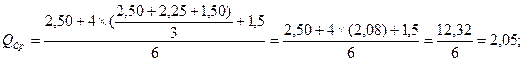
3) рассчитываем отклонение суммы рангов по каждому объекту экспертизы от средней:
1-ый: 2,05 – 2,50 = -0,45,
2-ой: 2,05 – 2,25 = -0,20,
3-ий: 2,05 – 1,50 = 0,55;
4) рассчитываем квадраты отклонений (0,2025, 0,04 и 0,3025 соответственно) и оцениваем сумму квадратов отклонений от среднего (S = 0,545).
5) определяем величину коэффициента конкордации Кендалла:

Очевидно, что мнение экспертов в данном случае является крайне слабо согласованным.
А какие результаты мы получим, применяя метод дисперсионных оценок мнений экспертов? Произведем соответствующие исчисления:
|
|
|
1) рассчитаем среднее значение суммарной оценки четырьмя экспертами трех объектов экспертизы:

2) определим фактическую дисперсию:
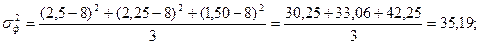
3) определим теоретическую дисперсию:
для этого необходимо предположить полную согласованность мнений экспертов, т.е. ситуацию в которой каждый из них первому виду риска (например) дал оценку в 0,25, второму – 0,5, третьему – 0,75. Тогда суммарная оценка первого риска будет составлять 1, второго – 2 и третьего – 3. Исходя из этого получим следующий результат:

4) определяем величину коэффициента конкордации по методу дисперсионных оценок мнений экспертов:

В данном случае мы получаем высокую согласованность мнения экспертов. Почему же получаются такие несоответствия если по конкордации экспертов если их оценивать разными методами? Дело в том, что первый метод применяется в том случае, когда эксперты определяют вероятность возникновения того или иного риска (т.е. в нашем случае это 25%, 50% и 75%), а второй метод применим только к тем ситуациям, когда эксперты определяют степень значимости риска по бально-рейтинговой системе, грубо говоря – расставляют их по местам в зависимости от их степени влияния. Так если в исходной таблице заменить вероятности на рейтинги (0,25 на 3, 0,5 на 2 и 0,75 на 1), то конкордация, рассчитанная вторым методом, будет оставлять 0,281, что так же, как и в первом случае, будет свидетельствовать о низкой согласованности экспертных мнений. Некоторая математическая погрешность между первым и вторым показателями будет возникать всегда и при любых исходных заданных условиях как следствие того, что в первом случае используются более точный данные, а во втором более обобщенные, но практически всегда результаты оценки будут находиться в одном интерпретационном интервале.
Задание для самостоятельного решения:
3. По нижеприведенным значениям оценки рисков экспертами необходимо определить согласованность их мнений методом Кендалла и методом дисперсионных оценок.
Условия для задания 3
| Номер оцениваемого риска | Оценка эксперта | ||||
| 1-го | 2-го | 3-го | 4-го | 5-го | |
| 0,25 | 0,25 | 0,5 | 0,5 | 0,75 | |
| 0,25 | 0,5 | 0,5 | 0,5 | 0,25 | |
| 0,5 | 0,5 | 0,75 | 0,5 | 0,5 | |
| 0,5 | 0,25 | 0,5 | 0,25 | 0,25 | |
| 0,75 | 0,5 | 0,75 | 0,25 | 0,5 | |
| 0,75 | 0,75 | 0,75 | 0,5 | 0,75 | |
| 0,5 | 0,25 | 0,25 | 0,5 | 0,75 | |
| 0,25 | 0,5 | 0,5 | 0,75 | 0,25 | |
| 0,75 | 0,5 | 0,75 | 0,75 | 0,5 | |
| 0,25 | 0,25 | 0,5 | 0,5 | 0,25 | |
| 0,5 | 0,5 | 0,25 | 0,25 | 0,5 | |
| 0,5 | 0,25 | 0,75 | 0,75 | 0,5 | |
| 0,5 | 0,75 | 0,25 | 0,25 | 0,25 | |
| 0,25 | 0,75 | 0,25 | 0,5 | 0,5 | |
| 0,75 | 0,5 | 0,75 | 0,75 | 0,75 |
|
|
|
Для выполнения данного задания студенту необходимо случайным образом выбрать не менее четырех рисков из представленных в таблице. Результаты оценки оформить письменно, сопроводив их развернутыми выводами.
|
|
|


