 |
Тема 1. Аналитическая геометрия на плоскости
|
|
|
|
Методические указания предназначены для студентов-заочников биологических специальностей.
При выполнении контрольных работ студент должен руководствоваться следующими указаниями:
1. Каждая работа должна выполняться в отдельной тетради (в клетку), на внешней обложке которой должны быть ясно написаны фамилия студента, его инициалы, полный шифр, специальность, номер контрольной работы.
2. Контрольные задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением каждой задачи надо полностью переписать ее условие. Решение задач следует излагать подробно.
3. На каждой странице тетради необходимо оставлять поля шириной 3 см. для замечаний преподавателя.
4. Контрольные работы должны выполняться самостоятельно. Если преподаватель установит несамостоятельное выполнение работы, то она не будет зачтена.
5. Получив прорецензированную работу (как зачтенную, так и незачтенную), студент должен исправить все отмеченные рецензентом ошибки и недочеты. В случае незачета по работе студент обязан в кратчайший срок выполнить все требования преподавателя, и представить работу на повторное рецензирование, приложив при этом первоначально выполненную работу.
6. Студент выполняет тот вариант контрольной работы, который совпадает с последней цифрой его учебного шифра (номер зачетки).
Таблица 1
| № варианта (последняя цифра зачётной книжки) | Номера задач для контрольной работы (если предпоследняя цифра зачётной книжки нечётная) (1,3,5,7,9) | |||||||
|
|
|
Таблица 2
| № варианта (последняя цифра зачётной книжки) | Номера задач для контрольной работы (если предпоследняя цифра зачётной книжки чётная) (0,2,4,6,8) | |||||||
Тема 1. Аналитическая геометрия на плоскости
Для решения задач по аналитической геометрии нам понадобятся следующие формулы:
1. Расстояние d между точками 
и 
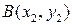на плоскости: 
(1)
2. Деление отрезка в данном отношении.
Даны точки и 
Координаты точки 
делящей отрезок АВ в отношении 
определяется по формулам: 
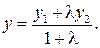
В частности, при делении отрезка пополам (
)
(2)
3. Все виды уравнений прямой.
а) уравнение прямой с угловым коэффициентом:
(3а),
где k – угловой коэффициент, b – отрезок на оси Оy, прямая не параллельна оси Оу.
б) уравнение прямой, проходящей через данную точку в данном направлении:
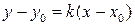(3б),
где k - угловой коэффициент, 
– координаты точки, лежащей на прямой, прямая не параллельна оси Оу.
в) уравнение прямой, проходящей через две данные точки:
= 
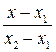(3в)
и 
– координаты данных точек, прямая не параллельна осям Ох и Оу;
г) уравнение прямой в отрезках:
(3г)
а – отрезок на Ох, b – отрезок на Оу, прямая не проходит через начало координат;
д) уравнение прямой, параллельной оси Оу:
х = а (3д)
где а – отрезок на Ох;
е) уравнение прямой, параллельной оси Оу:
|
|
|
у = b (3е),
где b – отрезок на Оу;
ж) общее уравнение прямой:
Ах + Ву + С = 0 (3ж)
А и В не равны нулю одновременно.
4. Угол φ, отсчитанный против часовой стрелки от прямой 
до прямой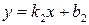 
определяется формулой:
(4)
а) Условие параллельности: 
б) Условие перпендикулярности: k2 =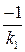 
5. Чтобы найти точку пересечения непараллельных прямых
А1x + B1y + С1= 0 и A2x + B2y + С 2= 0, нужно решить совместно их уравнения.
Задача 1: Даны координаты вершин треугольника АВС: А(4,3); В(16,-6); С(20,16). Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и ВС и их угловые коэффициенты; 3) угол В в радианах с точностью до двух знаков; 4) уравнение СD и ее длину; 5) уравнение медианы АЕ; 6) уравнение прямой, проходящей через точку С параллельно стороне АВ.
Решение: 1)Применяя (1), находим длину стороны
AB = 
= 
= 
= 15
2) Подставляя в (3,в) координаты точек А и В, получим уравнение стороны АВ:
= 
; 
= 
; 
= 
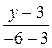4у – 12 = – 3х + 12; 3х + 4у – 24 = 0 (АВ)
Решая последнее уравнение относительно у, получим уравнение стороны АВ как уравнение прямой с угловым коэффициентом: 4у = – Зх + 24, у = 
х + 6, kAB = –3/4
Подставив в (3в) координаты точек В и С, получим уравнение прямой ВС: 
= 
; 
= 
; 
= 
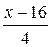11х – 2у – 188 = 0 (ВС) или у = 
х – 94, откуда kBC = 11/2, найдены: kАВ = –3/4; kBC = 11/2.
3) Искомый угол В образован прямыми АВ и ВС, угловые коэффициенты которых
tgB =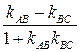 
= 
= 
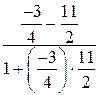= 2
Применяя (4), получим В = 63°26 или В = 1,11 рад.
4) Высота СD перпендикулярна стороне АВ.
Чтобы найти угловой коэффициент высоты СD, воспользуемся условием перпендикулярности прямых. Так как kAB = –3/4, то kCD = 4/3.
Подставив в (3б) координаты точки С и найденный угловой коэффициент 4/3 высоты, получим
(у – 16) = (4/3) (х – 20); 3у – 48 = 4х – 80; 4х – 3у – 32 = 0 (СD).
Чтобы найти длину высоты СD, определим координаты точки D– точки пересечения прямых АВ и СD.
Решая систему 
, находим х = 8, у = 0, т.е. D(8, 0).
По формуле (1) находим длину СD: СD = 
= 20
5) Чтобы найти уравнение медианы АЕ, определим координаты точки Е, которая является серединой отрезка ВС. Воспользуемся формулами деления отрезка пополам (2). Следовательно:
xE = 
= 18; yE =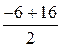 
= 5; E(18,5)
Подставив (3в) координаты точек А и Е, находим уравнение медианы:
= 
; 
= 
; x – 7y + 17 = 0 (AE)
6) Так как искомая прямая параллельна стороне АВ, то её угловой коэффициент равен угловому коэффициенту прямой АВ. Подставив в (3б) координаты точки С и угловой коэффициент k = –3/4, получим у–16 = (–3/4) (х – 20), 4у – 64 = –3х + 60, 3х + 4у – 124 = 0 (СL)
|
|
|
|
|
|
