 |
Вероятность события. Свойства вероятности
|
|
|
|
Вероятностью события А называется отношение числа mблагоприятных исходов к общему числу n всех элементарных равновозможных исходов. Вероятность события А обозначается Р(А).
Тогда, Р(А) = 
1) Р(А) = 0, если А – событие невозможное;
2) Р(В) = 1, если В – событие достоверное;
3) 0 < Р(С) < 1, если С - случайное событие;
4) Р(А+В) = Р(А) + Р(В), если А и В несовместные события;
5) Р(А)= 1 – Р(А)
Теоремы сложения и умножения вероятностей
Суммой двух событий А и В называется событие С, состоящее в появлении хотя бы одного из них: С = А + В.
Произведением событий А и В называется событие С = А·В, состоящее в совместном появлении этих событий.
Условной вероятностью Р(В/А) ((РA(В)) называется вероятность события В, вычисленная в предположении, что событие А уже произошло. События А и В называются независимыми, если вероятность события А не зависит от того, произошло или не произошло событие В, т.е. если Р(А/В) =Р(А) (условная вероятность равна безусловной).
Теорема 1. Вероятность произведения событий равна произведению вероятности одного из них на условную вероятность другого.
Р(А · В) = Р(В) · Р(А/В) = Р(А) · Р(В/А).
Следствие 1.1. Если события независимы, то вероятность их произведения равна произведению их вероятностей.
Р(А·В) = Р(В) · Р(А).
Теорема 2. Вероятность суммы двух совместных событий равна сумме их вероятностей без вероятности их произведения.
Р(А + В) = Р(А) + Р(В) – Р(А·В)
Следствие 2.1. Сумма вероятностей событий A1, A2 … An, образующих полную группу, равна единице:
Р(А1) + Р(А2) +... + Р(Аn) = 1.
Следствие 2.2 (Формула полной вероятности).
Вероятность события А, которое может наступить при условии появления одного из попарно несовместных событий B1, B2 ... Вn, образующих полную группу и называемых гипотезами, равна сумме произведений вероятностей каждого из них на соответствующую условную вероятность события А, т.е.:
|
|
|
Р(А) = Р(В1)·Р(А/В1) + Р(В2)·Р(А/В2) +... + Р(Вn)·Р(А/Вn).
Пример 1.
Вероятность заморозков в мае в некоторой местности 0,3.
Найти вероятность, что три дня подряд будут заморозки.
Решение.
Обозначим через В событие, состоящее в появлении трех дней с заморозками. Событие А = {день с заморозками} Р(А) = 0,3, В=А·А·А, тогда Р(В) = Р(А)·Р(А)·Р(А) = 0,3·0,3·0,3 = 0,027.
Схема Бернулли
Схемой Бернулли или схемой повторных независимых испытаний с двумя исходами: "успех" или "неуспех" называется последовательность n независимых испытаний, в каждом из которых "успех" наступает с одной и той же вероятностью р ≠ 0 и 1.
Вероятность того, что при n испытаниях «успех» наступит ровно k раз, вычисляется по формуле Бернулли: Pn(k) = Cnk · pk · qn-k ,
где n – число испытаний;
k – число "успехов";
p– вероятность "успеха" в одном испытании;
q = 1 – р– вероятность "неуспеха";
Cnk =  – число сочетании из n элементов пo k.
– число сочетании из n элементов пo k.
Пример 2.
Вероятность заболевания животного во время эпидемии 0,2. Найти вероятность, что из 6 животных 2 заболеют.
Решение.
Число животных n = 6, число "успехов" k = 2, р = 0,2, q =1 – 0,2 = 0,8.


При больших n использование формулы Бернулли затруднительно, поэтому, в этих случаях применяют приближенные формулы, которые следуют из локальной теоремы Лапласа и из теоремы Пуассона.
Выбор формулы для решения задачи на схему Бернулли поможет сделать следующая таблица:
| Название формулы | Формула | Когда даст хорошее решение. |
| Формула Бернулли. | Рn(k) = Cnk · pk · qn-k | Для всех n и р |
| Формула, следующая из локальной теоремы Лапласа. | Рn(k)≈ 

| При р > 0,1 или nр > 9. |
| Формула, следующая из теоремы Пуассона. | 
| р ≤ 0,1; nр < 9, n > 10. |
Имеются таблицы, в которых помещены значения функции
|
|
|
φ(х) = 
Свойства функции φ(х):
1) φ(–х) = φ(х);
2) при х > 4 φ(х) ≈ 0.
Пример 3.
Допустим, укореняют 15 черенков роз. Приживаемость 80%. Найти вероятность того, что из 15 черенков укоренится ровно 12.
Решение,.
n = 15; k = 12; р = 0,8; q = 1 – 0,8 = 0,2.
Имеем nрq = 15·0,8·0,4 = 2,4
 ;
;
Интегральная теорема Лапласа.
Вероятность того, что в п независимых испытаниях, проведенных по схеме Бернулли, событие наступит не менее k1 и не более k2 раз, приближенно равна
Р(k, k2) ≈ Ф(х2) – Ф(х1),
где Ф(х) =  - интегральная функция Лапласа.
- интегральная функция Лапласа.
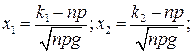
Значение функции Лапласа занесены в таблицу.
Свойства функции Ф(х):
1)Ф(–х) = –Ф(х);
2) если х > 5, то Ф(х) ≈ 0,5.
Пример 4.
Вероятность того, что подготовка почвы к посеву выполнена с соблюдением требований агротехники 0,75. Найти вероятность того, что из 100 делянок почва подготовлена к посеву не меньше чем на 70 и не больше чем на 80.
Решение.
По условию, р = 0,75; q = 1 – 0,75 = 0,25; n = 100; k1 =100, k2 =80.
Р100(70,80) = Ф(x2) – Ф(х1)


Таким образом, имеем
Р100(70,80) = Ф(1,15) – Ф(–1,15) = Ф(1,15) + Ф(1,15) = 2Ф(1,15).
По таблице находим Ф(1,15) = 0,3749.
Искомая вероятность Р100(70,80) = 2·0,3749 = 0,7498.
|
|
|


