 |
Тема 2. Производная функции
|
|
|
|
Производной функции у = f(х) в точке x0 называется предел отношения приращения функции к приращению аргумента при условии, что последнее стремится к нулю.
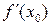 =
= 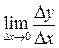 =
= 
∆у = f(х) - f(х0) - приращение функции, ∆х = х – х0 - приращение аргумента.
Обозначается производная: 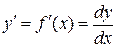
Символ dу называют дифференциалом функции и вычисляют по формуле:
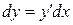 или
или 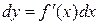
Операция нахождения производной называется дифференцированием функции.
Основные правила дифференцирования.
Пусть U = U(х) и V = V(х) — функции, дифференцируемые в некоторой точке х0,
С = сопst (постоянная величина), тогда:
1) CI = 0
2) (U ± V)I= UI ± VI
3) (U · V) = UI · V + VI · U
4) (CU)I = CUI
5) 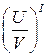 =
= 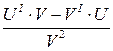
Таблица производных 1:
| 1. (хα)I = α · xα-1 xI = 1 | 7. (cos x)I = -sin x |
(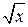 )I = )I = 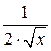
| 8. (tgx)I = 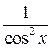
|
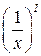 = = 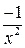
| 9. (ctgx)I = 
|
| 2. (ax)I = ax · ln a | 10. (arcsin x)I = 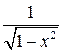
|
| 3. (ex)I = ex | |
4. (log a x)I = 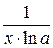
| 11. (arccosx)I = 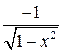
|
| 6. (sin x)I = cos x | 11. (arccos x)I = 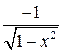
|
12. (arctgx)I = 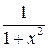
| 13. (arcctgx)I = 
|
Производная сложной функции
Пусть у – сложная функция, т.е. у = f(u), u = g(х), или у = f (g(x)) (f – внешняя функция, g – внутренняя функция).
Производная сложной функции равна произведению производной внешней функции в своей точке на производную внутренней функции.
Для вычисления производной сложной функции применяют таблицу 2.
Таблица производных (сложной функции) 2
| 1. (uα)I = α · uα-1 · uI | 9. (ctg u)I = 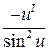
|
| 2. (au)I = au · ln a · uI | |
| 3. (eu)I = eu · uI | |
4. (loga · u)I = 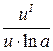
| 10. (arcsin u)I = 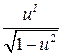
|
5. (ln u)I = 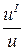
| 11. (arcos u)I = 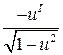
|
| 6. (sin u)I = cos u · uI | 12. (arctgu)I = 
|
| 7. (cos u)I = -sin u · uI | |
8. (tgu)I = 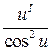
| 13. (arcctgu)I = 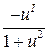
|
Тема 3. Интеграл
Функция F(х) называется первообразной для функции f(х), если FI(х) = f(х). Всякая непрерывная функция f(х) имеет бесконечное множество первообразных функций, которые отличаются друг от друга на постоянную. Неопределенным интегралом от функции f(х) называется совокупность всех ее первообразных.
|
|
|
Обозначают:  = F(x)+с
= F(x)+с
Свойства неопределенного интеграла.
1. 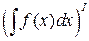 = f(x) или d
= f(x) или d 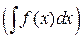 = f(x) dx
= f(x) dx
2. 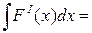 F(x)+c или
F(x)+c или 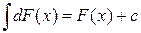
3. 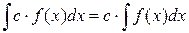
т.е. постоянный множитель можно выносить за знак интеграла.
4.  , т.е. неопределенный интеграл от алгебраической суммы равен сумме интегралов.
, т.е. неопределенный интеграл от алгебраической суммы равен сумме интегралов.
Таблица основных интегралов
1. 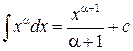 (α≠-1) (α≠-1) 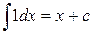
| |
2. 
| 3. 
|
4. 
| 5. 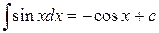
|
6. 
| 7. 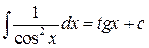
|
8. 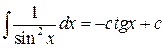
| |
9. 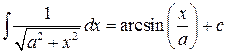 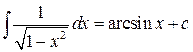
| |
10. 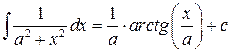 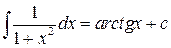
| |
11. 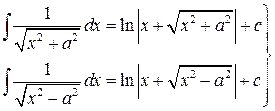 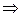
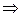 (формула «длинного» логарифма) (формула «длинного» логарифма)
| |
12.  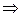
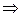 (формула «высокого» логарифма) (формула «высокого» логарифма)
|
Найти интеграл:
Воспользуемся свойствами 3 и 4:
а) 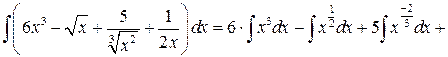
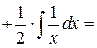 воспользуемся табличными интервалами 1и 2:
воспользуемся табличными интервалами 1и 2:
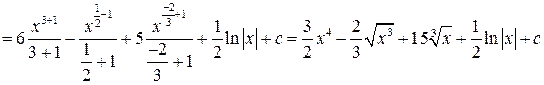
Тема 4. Теория вероятностей
Основы комбинаторики
Факториалом целого положительного числа n (обозначается n!) называется произведение 1·2·3·...·n = n! По определению 0!=1.
Основной закон комбинаторики. Пусть нужно произвести k действий, причем первое действие можно произвести n1 способами, второе – n2способами,... k-ое – nk способами. Тогда все действия можно произвести n1 · n2 ·... · nk способами.
Перестановкой из n элементов называется набор из n элементов, расположенных в определенном порядке. Число всех перестановок из n элементов равно: Рn = n!
Размещением из n элементов по k элементов называется набор из к элементов, выбранных из данных n элементов в определенном порядке, т.е. два различных размещения отличаются либо составом элементов, либо (при одинаковом составе) порядком элементов.
Число всех размещений из n элементов по к элементов равно:
Ank = 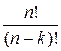
Сочетанием из n элементов по k элементов называется набор из k элементов, выбранных из данных n элементов в произвольном порядке, т.е. два различных сочетания отличаются только составом элементов.
Число всех сочетаний из n элементов по к элементов равно:
Сnk = 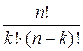
Основное свойство сочетаний: Сnk = Сnn-k
Основные понятия теории вероятностей
Испытанием называется осуществление ряда условий, при которых производится наблюдение.
|
|
|
Событие - это результат испытания.
Элементарными событиями (исходами) называются возможные, исключающие друг друга, результаты одного испытания.
Событие называется достоверным, если при испытании оно обязательно произойдет.
Событие называется невозможным, если при испытании оно не может произойти.
Событие называется случайным, если при испытании оно может либо произойти, либо не произойти.
События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.
События называются единственно возможными, если появление в результате испытания одного и только одного из них является достоверным событием. Единственно возможные события попарно несовместны.
События называются равновозможными, если есть основание считать, что ни одно из этих событий не является более возможным, чем другие.
Полной группой называется совокупность единственно возможных событий испытания.
Событие 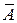 , которое состоит в том, что событие А не происходит, называется противоположным событию А. Очевидно, события А и
, которое состоит в том, что событие А не происходит, называется противоположным событию А. Очевидно, события А и 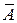 образуют полную группу событий.
образуют полную группу событий.
|
|
|


