 |
Тема 8. Статистические оценки параметров распределения.
|
|
|
|
Математическая статистика - наука, занимающаяся разработкой методов получения, описания и использования статистических данных с целью изучения закономерностей, присущих массовым случайным явлениям. Многие задачи статистики связаны с исследованием и контролем количественных и качественных показателей продукции того или иного конкретного производства. В основе их решения лежит выборочный метод, сущность которого состоит в следующем. Обследуется распределение какого-либо признака для весьма большой совокупности объектов. Сделать это для каждого объекта совокупности практически невозможно, поэтому исследуют часть её - выборку. Очевидно, что по выборочным характеристикам можно судить обо всей совокупности только приближённо. Одной из задач статистики является оценка параметров распределения случайной величины по данным выборки. В качестве оценки генеральной средней (среднего значения признака на всей совокупности объектов, подлежащих обследованию) служит выборочная средняя (среднее значение признака на части элементов генеральной совокупности, случайно отобранных из неё), а в качестве оценки дисперсии генеральной совокупности используют исправленную выборочную дисперсию. Если случайная величина имеет нормальное распределение, то в этом случае становится возможным применять так называемые интервальные оценки. Доверительным интервалом называется найденный по данным выборки интервал (Θ – δ, Θ + δ), который покрывает оцениваемый параметр Θ с заданной надёжностью γ. Надёжность γ обычно принимают равной 0,95 или 0,99, или 0,999. Конечно, нельзя категорически утверждать, что найденный доверительный интервал покрывает параметр Θ. Но в этом можно быть уверенным на 95% при γ = 0,95, на 99% при γ = 0,99 и т.д. Это значит, что если сделать много выборок, то для 95% из них (если, например, γ = 0,95) вычисленные доверительные интервалы покрывают параметр Θ.
|
|
|
Задача. Для определения средней урожайности сахарной свеклы в совхозе на площади 1000 га была определена её урожайность на 100 га. Результаты выборочного обследования представлены следующим распределением:
| Урожайность, ц/га | 23-25 | 25-27 | 27-29 | 29-31 | 31-33 | 33-35 | 35-37 |
| Площадь, га |
Найти: 1) величину, которую следует принять за среднюю урожайность на всём массиве;
2) величину, которую следует принять за среднее квадратичное отклонение урожайности на всём массиве;
3) доверительный интервал в котором с вероятностью 0,95 заключена средняя урожайность на всём массиве.
Решение.
1) В качестве приближённого значения средней урожайности на всём массиве принимаем среднюю арифметическую данного в условии распределения, т.е. выборочную среднюю:
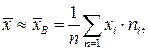(n = n1 + n2 +...+ nk).
За значение признака нужно принять середины интервалов. Получим:
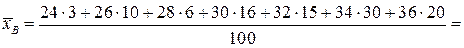
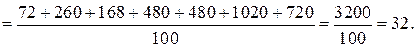
Значит, приближённое значение средней урожайности на всём массиве будет х ~ 32 ц.
2) Для оценки дисперсии генеральной совокупности применяем формулу
Sn2 =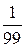 
· (3(24 - 32)2 + 10(26 - 32)2 + 6(28 - 32)2+ 16(30 - 32)2 + 15(32 - 32)2 + 30(34 - 32)2 + + 20(36 - 32)2) = 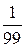· (192 + 360 + 96+ 64 + 0 + 120 + 320) = 
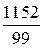= 11,64.
Значит, приближённое значение дисперсии на всём массиве будет, σ ~ 11,64, отсюда среднее квадратичное отклонение урожайности на всём массиве равно S = 
= 3,4. Найдём среднее квадратичное отклонение выборочной средней по формуле σх = Sx = Sn/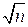 
.
Получим 
Итак, оценка средней урожайности сахарной свеклы на всём массиве равна 32 ц со средней квадратичной ошибкой 0,34 ц. Оценка среднего квадратичного отклонения урожайности на всём массиве равна 3,4 ц.
3) Для вычисления доверительного интервала воспользуемся равенством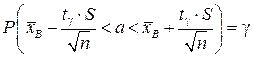 
,
|
|
|
согласно которому можно утверждать, что с надёжностью у доверительный интервал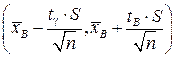 
покрывает неизвестное математическое ожидание, точность оценки: 
.
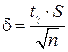Поскольку n = 100 > 30, то пользуемся нормальным распределением. Значит,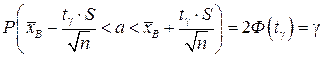 
.
Из равенства 2Ф(tγ) = 0,95 следует Ф(tγ) = 0,475 и по таблице 3 приложения находим1,96. Следовательно, точность оценки
.
Концы доверительного интервала
хв – δ = 32 – 0,67 = 31,33 и хв + δ = 32 + 0,67 – 32,67.
Таким образом, с вероятностью 0,95 средняя урожайность сахарной свёклы на всём массиве заключена в границах от 31,33 ц до 32,67 ц.
|
|
|
