Билет №2 Логические исчисления. Графы. Алгоритмы. Языки и грамматики. Автоматы.

Билет №1 Роль математики в познании мира. Дискретная математика.

Дискретная математика – область математики, изучающей свойства дискретных структур, которые возникают как в пределах самой математики, так и в ее приложениях. К таким структурам могут быть отнесены конечные группы, конечные графы, а также некоторые математические модели преобразователей информации, конечные автоматы, машины Тьюринга и так далее. Свойства дискретных структур: - конечные структуры; - конечные графы; - некоторые математические модели преобразователей информации; - конечные автоматы; - машины Тьюринга;... Дискретность – это прерывность. Дискретная математика – отрасль математики, которая изучает проблемы, касающиеся конечных множеств. Дискретная математика является одной из содержательных частей информатики, а именно теоретической части. Разделы дискретной математики: Математическая логика, математическая кибернетика, общая алгебра, теория графов, теория алгоритмов, теория игр, теория кодирования, теория конечных автоматов, теория формальных грамматик, вычислительная геометрия, теория булевых функций, логическое программирование, функциональное программирование, лямбда-исчисление, булева алгебра, комбинаторика.

Роль математики в современном мире. Целью изучения математики является повышение общего кругозора, культуры мышления, формирование научного мировоззрения. Математика – наука о количественных отношениях и пространственных формах действительного мира. Выделяют 4 периода развития математики: зарождение математики, элементарная математика, математика переменных величин, современная математика. Начало периода элементарной математики относят к VI-V веку до нашей эры. Был накоплен к этому времени достаточно большой фактический материал. Понимание математики, как самостоятельной науки возникло впервые в Древней Греции.
В течение этого периода математические исследования имеют дело лишь с достаточно ограниченным запасом основных понятий, возникших для удовлетворения самых простых запросов хозяйственной жизни. Развивается арифметика – наука о числе.
В период развития элементарной математики появляется теория чисел, выросшая постепенно из арифметики. Создается алгебра, как буквенное исчисление. Обобщается труд большого числа математиков, занимающихся решением геометрических задач в стройную и строгую систему элементарной геометрии – геометрию Евклида, изложенную в его замечательной книге «Начала» (300 лет до н. э.).
В XVII веке запросы естествознания и техники привели к созданию методов, позволяющих математически изучать движение, процессы изменения величин, преобразование геометрических фигур.
С употребления переменных величин в аналитической геометрии и создание дифференциального и интегрального исчисления начинается период математики переменных величин. Великим открытиям XVII века является введенная Ньютоном и Лейбницем понятие «бесконечно малой величины», создание основ анализа бесконечно малых (математического анализа).
На первый план выдвигается понятие функции. Функция становится основным предметом изучения. Изучение функции приводит к основным понятиям математического анализа: пределу, производной, дифференциалу, интегралу.
К этому времени относятся и появление гениальной идеи Р. Декарта – метода координат. Создается аналитическая геометрия, которая позволяет изучать геометрические объекты методами алгебры и анализа. С другой стороны метод координат открыл возможность геометрической интерпретации алгебраических и аналитических фактов.
Дальнейшее развитие математики привело в начале ХIX века к постановке задачи изучения возможных типов количественных отношений и пространственных форм с достаточно общей точки зрения.
Связь математики и естествознания приобретает все более сложные формы. Возникают новые теории. Новые теории возникают не только в результате запросов естествознания и техники, но и в результате внутренней потребности математики. Замечательным примером такой теории является «воображаемая геометрия» Н. И. Лобачевского. Развитие математики в XIX и XX веках позволяет отнести ее к периоду современной математики. Развитие самой математики, «математизация» различных областей науки, проникновение математических методов во многие сферы практической деятельности, прогресс вычислительной техники привели к появлению новых математических дисциплин, например, исследование операций, теория игр, математическая экономика и другие.
В основе построения математической теории лежит аксиоматический метод. В основу научной теории кладутся некоторые исходные положения, называемые аксиомами, а все остальные положения теории получаются, как логические следствия аксиом.
Основными методами в математических исследованиях являются математические доказательства – строгие логические рассуждения.

Билет №2 Логические исчисления. Графы. Алгоритмы. Языки и грамматики. Автоматы.

ЛОГИЧЕСКИЕ ИСЧИСЛЕНИЯ
формализации содержательных логич. теорий; выводимые объектыЛ. п. интерпретируются как суждения, составленные из простейших (имеющих, вообще говоря, субъектно-предикатную структуру) при помощи пропозициональных связок и кванторов. Чаще всего используютсясвязки "не", "и", "или", "если..., то..." и кванторы существованиях и всеобщности. От произвольных исчислений

Л. и. отличаются чисто логич. характером интерпретаций и правил вывода, от логико-математическихисчислений - отсутствием в языке символов конкретных математич. предикатов и функций (за исключениемсимвола добавление к-рого интерпретируется как введение в рассмотрение равенства и не считаетсяобычно нарушающим логич. характер исчисления). Сформулированные отличия носят относительныйхарактер, т. к. Л. и. остаются чисто формальными системами, и любая возможная их интерпретация исемантика должны рассматриваться как нечто внешнее, имеющее эвристическую, а не доказательнуюценность при научении свойств исчисления.

Одно из важнейших Л. и. - классическое исчисление предикатов с функциональными знаками.

Кроме того, это исчисление имеет три правила вывода: "из Аи 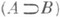можно получить В", "из 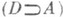можно получить 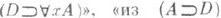можно получить 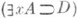". Доказуемыми формулами(или теоремам и) рассматриваемого исчисления наз. любые формулы, к-рые могут быть получены из аксиом исчисления в результате применения (возможно, многократного) указанных правил (см. Вывод логический).

Граф это множество точек или вершин и множество линий или ребер, соединяющих между собой все или часть этих точек. Вершины, прилегающие к одному и тому же ребру, называются смежными.
Если ребра ориентированны, что обычно показывают стрелками, то они называются дугами, и граф с такими ребрами называется ориентированным графом.
Если ребра не имеют ориентации, граф называется неориентированным. Графы обычно изображаются в виде геометрических фигур, так что вершины графа изображаются точками, а ребра - линиями, соединяющими точки. 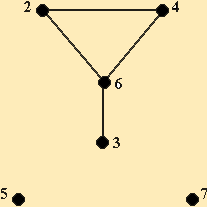Петля это дуга, начальная и конечная вершина которой совпадают. Простой граф граф без кратных ребер и петель. Степень вершины это удвоенное количество петель, находящихся у этой вершины плюс количество остальных прилегающих к ней ребер. Пустым называется граф без ребер. Полным называется граф, в котором каждые две вершины смежные.

Алгоритм - точное предписание исполнителю совершить определенную последовательность действий для достижения поставленной цели за конечное число шагов. Поэтому обычно формулируют несколько общих свойств алгоритмов, позволяющих отличать алгоритмы от других инструкций. Такими свойствами являются: • Дискретность • Определенность • Результативность (конечность) • Массовость

Виды алгоритмов: • Механические алгоритмы • Гибкие алгоритмы • Вероятностный • Эвристический • Линейный алгоритм • Разветвляющийся алгоритм • Циклический алгоритм

Вспомогательный

Требования:

Первое правило – при построении алгоритма прежде всего необходимо задать множество объектов, с которыми будет работать алгоритм.

Второе правило – для работы алгоритма требуется память. В памяти размещаются входные данные, с которыми алгоритм начинает работать, промежуточные данные и выходные данные, которые являются результатом работы алгоритма

Третье правило – дискретность. Алгоритм строится из отдельных шагов (действий, операций, команд). Множество шагов, из которых составлен алгоритм, конечно.

Четвертое правило – детерменированность. После каждого шага необходимо указывать, какой шаг выполняется следующим, либо давать команду остановки. Пятое правило – сходимость (результативность). Алгоритм должен завершать работу после конечного числа шагов. При этом необходимо указать, что считать результатом работы алгоритма.

Коротко говоря, формальный язык — это математическая модель реального языка. Под реальным языком здесь понимается некий способ коммуникации (общения) субъектов друг с другом.

Основные принципы: 1)Обобщение (абстрагирование). Объекты изучения в математике — это специальные сущности, которые существуют только в математике и предназначены для изучения математиками. 2)Строгость рассуждений. В науке принято для выяснения истинности того или иного рассуждения сверять их результаты с тем, что существует в действительности, т.е. проводить эксперименты.

Виды грамматик:

Распознающие грамматики. Такие грамматики представляют собой устройства (алгоритмы), которым на вход подается цепочка языка, а на выходе устройство печатает «Да», если цепочка принадлежит языку, и «Нет» — в противном случае.

Порождающие грамматики. Этот вид устройств используется для порождения цепочек языков по требованию. Образно говоря, при нажатии кнопки будет сгенерирована некоторая цепочка языка.

Перечисляющие грамматики. Такие грамматики печатают одну за другой все цепочки языка. Очевидно, что если язык состоит из бесконечного числа цепочек, то процесс перечисления никогда не остановится. Хотя, конечно его можно остановить принудительно в нужный момент времени, например, когда будет напечатана нужная цепочка.

Автоматы: На протяжении последних десятилетий велись и ведутся интенсивные работы по созданию и использованию различных систем и устройств для переработки дискретной информации. Преобразователи дискретной информации широко используются в качестве различного рода технических автоматов, вычислительных устройств и их функциональных блоков, устройств управления роботами, управляющих объектами по заданному алгоритму. Широкий класс таких преобразователей объединяется под общим названием -автоматы. Эти устройства имеют конечное число входов, воспринимающих информацию, и конечное число выходов для выдачи переработанной информации. Зависимость между входами и выходами задается предписанным алгоритмом переработки информации. Информация на входе и выходе представляется символами, физическими носителями которых являются квантованные по времени сигналы. Теория автоматов - это раздел теории управляющих систем, изучающий математические модели преобразователей дискретной информации, называемые автоматами. Конечный автомат (рис.2б) — математическая абстракция, позволяющая описывать пути изменения состояния объекта в зависимости от его текущего состояния и входных данных, при условии, что общее возможное количество состояний Q и множество входных сигналов Z конечны. Конечный автомат является частным случаем абстрактного автомата.