 |
Вопрос 9 (Методы решения систем линейных и алгебраических уравнений)
|
|
|
|
Матричный метод
Х=А-1В
= 1/∆ 
Матричным методом можно решить системы, в которых число уравнений совпадает с числом неизвестных и ∆≠0
Метод Крамера
Хi=∆i/∆, где i=1,2…n
∆ - определитель главной матрицы
∆ - определитель, полученной заменой i столбца, столбцом свободных членов
Если определитель системы не равен 0, то система имеет единственное решение.
Если ∆=0, система имеет множество решений, либо не имеет решений, если хотя бы один из ∆i≠0
Метод Гаусса
Прямой ход: система приводится к ступенчатому виду с помощью последовательного исключения элементов
Обратный ход: последовательно определяем неизвестные из этой системы, подставляем найденные в предыдущие уравнения.
Вопрос 10 (Линейные пространства. Базис и размерность линейного пространства)
Лине́йное простра́нство, или ве́кторное простра́нство, является обобщением понятия совокупности всех векторов n-мерного пространства. Линейные пространства — основной объект изучения линейной алгебры.
Пусть V - непустое множество (его элементы будем называть векторами и обозначать 
...), в котором установлены правила:
любым двум элементам 
соответствует третий элемент 
называемый суммой элементов 
(внутренняя операция);
каждому 
и каждому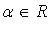 
отвечает определенный элемент 
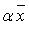(внешняя операция).
Множество V называется действительным линейным (векторным) пространством, если выполняются аксиомы:
(нулевой элемент, такой, что 
).
(элемент, противоположный элементу 
), такой, что 
Если любой вектор системы векторов линейного пространства линейно выражается через остальные векторы системы, то система векторов называется линейно зависимой.
|
|
|
Векторное пространство Rn называется n-мерным, если в нем можно найти n линейно независимых векторов.
Размерность – максимальное число содержащихся в данном линейном пространстве линейно независимых векторов.
Базис – совокупность n линейно независимых векторов в Rn
Пространство, имеющее конечную размерность называется конечно-мерным. Пространство, в котором можно найти сколь угодно много линейно независимых векторов, называется бесконечномерным.
Вопрос №11
Линейные преобразования. Линейные операторы. Характеристические числа и собственные векторы линейного преобразования.
Линейное преобразование – отображение векторного пространства в себя, при котором суммой двух векторов является сумма их образов, а образом произведения вектора на число – произведение образа вектора на это число.
Линейное преобразование называется тождественным, если оно преобразует любой вектор Х в самого себя.
Линейный оператор – это линейное отображение линейного пространства в себя.
Нарушение любого из этих условий означает, что отображение(оператор) не является линейным:
Оператор, переводящий любой вектор линейного пространства R в нулевой вектор пространства, является линейным оператором. Такой оператор наз. нулевым.
Оператор, который каждому вектору пространства R ставит в соответствие сам вектор, является линейным и наз. единичным.
Растяжение (сжатие) векторов пространства R в одно и то же число K раз является так же линейным оператором. Такой оператор наз. оператором подобия.
Оператор, который каждый вектор поворачивает вокруг некоторой точки О в одну и ту же сторону на угол α, является линейным и наз. оператором вращения.
Преобразование А наз. Линейным, если для любых векторов X и Y и для любого действительного числа ʎ выполняются равенства:
А(X+Y)=Ах+Аy, А(ʎх)=ʎАx
Линейное преобразование наз. тождественным, если оно преобразует любой вектор X в Самого себя. (Е - обозн-е), следовательно Ех=Х 
|
|
|
Пусть R-заданное n-мерное линейное пространство. Нулевой вектор х 
R наз-ся собственным вектором линейного преобразования А, если найдется такое ʎ, что выполняется равенство
Ах=ʎх (ʎ-характеристическое число)
Линейно независимые собственные векторы, отвечающие одному и тому же характеристическому числу образуют базис некоторого «собственного» подпространства, каждый вектор которого есть собственный вектор при том же. В частности, каждый собственный вектор порождает одномерное собственное подпространство, «собственное направление».
Однако, если собственные векторы операторсоответствуют различным характеристическим числам, то линейная комбинация этих собственных векторов не будет собственным вектором оператора.
Вопрос №12
Евклидово пространство. Ортогональный базис.
Ортогональный базис — ортогональная (ортонормированная) система элементов линейного пространства со скалярным произведением, обладающая свойством полноты.
Ортогональный базис — базис, составленный из попарно ортогональных векторов.
Ортогональный базис — система попарно ортогональных элементов 
гильбертова пространства 
такая, что любой элемент 
однозначно представим в виде сходящегося по норме ряда
называемого рядом Фурье элемента 
по системе 
.
Часто базис выбирается так, что 
, и тогда он называется ортонормированным базисом. В этом случае числа 
, называются коэффициентами Фурье элемента по ортонормированному базису , имеют вид
.
Необходимым и достаточным условием того, чтобы ортонормированная система была базисом, является равенство Парсеваля.
Гильбертово пространство, имеющее ортонормированный базис, является сепарабельным, и обратно, во всяком сепарабельном гильбертовом пространстве существует ортонормированный базис.
Если задана произвольная система чисел 
такая, что 
, то в случае гильбертова пространства с ортонормированным базисом ряд 
— сходится по норме к некоторому элементу . Этим устанавливается изоморфизм любого сепарабельного гильбертова пространства пространству 
(теорема Рисса — Фишера).
Ортогональный набор векторов который является базисом, наз. ортогональным базисом.
|
|
|
Линейное пространство R наз. евклидовым, если имеется правило, которое позволяет для каждых 2х векторов X и Y из R построить действ-ое число, наз. скалярным произведением векторов X и Y и обозначаемое (X;Y), причем это правило удовлетворяет следующим условиям.
(х;у)=(у;х)
(х;у+z)=(x;y)+(x;z)
(ʎx;у)=ʎ(х;у)
(х;х)>0, если х≠0
Вопрос № 13
Приведение квадратичной формы к каноническому виду.
Квадратичная форма — функция на векторном пространстве, задаваемая однородным многочленом второй степени от координат вектора.
Элементарным способом приведения квадратичной формы к каноническому виду является метод Лагранжа.
Данный метод состоит в последовательном выделении в квадратичной форме полных квадратов. Пусть задана квадратичная форма:
В силу симметричности матрицы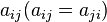 
квадратичную форму можно переписать следующим образом:
Возможны два случая:
хотя бы один из коэффициентов 
при квадратах отличен от нуля. Не нарушая общности, будем считать 
(этого всегда можно добиться соответствующей перенумерацией переменных);
все коэффициенты 
, но есть коэффициент 
, отличный от нуля (для определённости пусть будет 
).
В первом случае преобразуем квадратичную форму следующим образом:
, где
, а через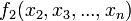 
обозначены все остальные слагаемые.
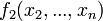представляет собой квадратичную форму от n-1 переменных 
.
С ней поступают аналогичным образом и так далее.
Заметим, что 
Второй случай заменой переменных 
сводится к первому.
Вопрос № 14
Векторы. Линейные операции над векторами. Линейная зависимость векторов R2 и R3.
Вектор- направленный прямолинейный отрезок.
Длиной или модулем вектора АВ наз. длина вектора АВ и обознач. IАВI или IаI
Вектор, длина которого равна нулю- нулевой вектор. Вектор, длина которого равна 1 обознач. Е(е).
Векторы называются компланарными, если существует плоскость, которой они параллельны.
Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.
|
|
|
Линейные операции над векторами:
Под линейными операциями над векторами понимают операции сложения, вычитания и умножения вектора на число.
Сложение векторов 
= 
+ 
Метод треугольника
Правило параллелограмма
Вектор, лежащий на другой диагонали этого параллелограмма, направленный в сторону уменьшаемого, будет задавать разность векторов.
Сложение 3х или более векторов выполняется последовательным откладыванием векторов, равных данным.
Произведением вектора а на число k называют вектор аk, который имеет длину IkI*IaI, коллинеарен вектору а и имеет направление вектора а, если k>0 и противополож. ему если k<0.
= - можно получить = +(- )
Метод треугольника
Метод параллелограмма
Свойства:
В=ʎа, то вIIа (верно и наоборот)
А=IaI* 
, следовательно = 
Свойства операции:
а+в=в+а
(а+в)+с=а+(в+с)
ʎ1*(ʎ2*а)=ʎ1*ʎ2*а
(ʎ1+ʎ2)*а=ʎ1*а+ʎ2*а
ʎ*(а+в)=ʎ*а+ʎ*в
Линейная зависимость- это свойство, которое может иметь подмножество линейного пространства. Для этого должна существовать нетривиальная линейная комбинация элементов этого множества, равная нулевому элементу.
a1`, a2`,…, an`; Вектора называются линейно-независимыми, если равенствоλ1 a1` + λ2 a2` +…+λn an` = 0выполняется только в тревиальном случае – λ1a1`+λ2 a2`+…+λn an` = 0, λ1, λ2, λ3…λn=0; и называются линейно-зависимыми, если хотя бы одно из чисел λ<>0;
λ1<>0; μ1=λ2/λ1; μ2=λ3/λ2…; a1`= μ1 a2`+μ2 a3` +…+μ(n - 1)an`;
Вектор a1` представлен линейной комбинацией векторов.
Докажем следующую ТЕОРЕМУ: Всякие 3 вектора на плоскости линейно зависимые. Дано:a`, b`, c`, причем 2 из них колинеарны. Док-ть:a`=λ1 b`+λ2 c`-?; Док-во:1) пустьa` иb` колинеарны:a`=λ1 b` + 0 c`; λ1<>0; λ2=0; c`=λ1 a`+λ2 b`=|b`=αa`|=λ1 a`+λ2 α a` = β a` + 0 b`; 2) Дано: a`, b`, c`; c`=λ1 a`+λ2 b`; Док-во:c`=OM`; OM` = OM1`+OM2`; OM1`=λ1 a`; OM2`=λ2 b`; c`=λ1 a` + λ2 b`
Следствие: 1. Максимальное число линейно-независимых векторов на плоскости равно двум. 2. Для того, чтобы 2
вектора на плоскости были линейно-независимы <=>, чтобы они были неколлинеарными.
Линейная зависимость векторов в трехмерном пространстве. Вектора, лежащие в одной плоскости или параллельных плоскостях называются компланарными. ТЕОРЕМА: любые 4 вектора в 3х-мерном пространстве являются линейно-зависимыми. Дано:a`, b`, c`, d`; из них 3 компланарны; a` =λ1 b` +λ2 c` +0` d` (см. рисунок).
OM`= a`; a` ^ b`; d` ^ b`; b` ^ c`; ON – проекция
ON`= OM2+ON3; NM`=OM1`;
OM`=ON`+NM`; OM`=OM1`+OM2`+OM3`
OM1`=λ1 d`; OM2`=λ2 b`; OM3 = λ3 c`;
Это означает, что векторы линейно-зависимые.
Следствие:
1. Максимальное число линейно-независимых
векторов в трехмерном пространстве равно 3м.
2. Для того, чтобы 3 вектора в трехмерном пространстве были линейно-независимые <=>, чтобы они были не компланарны.
|
|
|
Базис линейного пространства является в частности множеством линейно независимых векторов.
(насчет зависимости векторов в R2 и R3 не знаю, это все, что нашла)
Вопрос № 15
Базис. Декартова система координат. Координаты вектора. Длина вектора. Направляющие косинусы вектора. Проекция вектора на ось.
Ба́зис - множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества — базисных векторов.
Декарт впервые ввел координатную систему, которая существенно отличалась от общепринятой в наши дни.Он использовал косоугольную систему координат на плоскости, рассматривая кривую относительнонекоторой прямой с фиксированной системой отсчета. Положение точек кривой задавалось с помощьюсистемы параллельных отрезков, наклонных или перпендикулярных к исходной прямой. Декарт не вводилвторой координатной оси, не фиксировал направления отсчета от начала координат. Только в 18 в.сформировалось современное понимание координатной системы, получившее имя Декарта.
Для задания декартовой прямоугольной системы координат выбирают взаимно перпендикулярные прямые,называемые осями. Точка пересечения осей O называется началом координат. На каждой оси задаетсяположительное направление и выбирается единица масштаба. Координаты точки P считаютсяположительными или отрицательными в зависимости от того, на какую полуось попадает проекция точки P.
Координаты вектора ― коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору.
Разложение вектора по базису имеет вид: 
Свойства координат вектора.
1. Любые равные векторы в единой системе координат имеют равные координаты.
2. Координаты коллинеарных векторов пропорциональны. При условии, что ни один из векторов не равен нулю.
3. Квадрат длины любого вектора равен сумме квадратов его координат.
4.При операции умножения вектора на действительное число каждая его координата умножается на это число.
5. При операции сложения векторов вычисляем сумму соответствующие координаты векторов.
6. Скалярное произведение двух векторов равняется сумме произведений их соответствующих координат.
Длиной вектора называется арифметическое значение квадратного корня и скалярного квадрата. 
Длина вектора удовлетворяет следующим условиям:
1. 
, если 
2. 
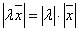
3. 
- неравенство Коши-Буня
4. 
- неравенство треугольника
Направляющими косинусами вектора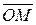 
называются
, 
, 
,
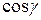где 
– углы, которые составляет вектор 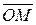с осями координат (они определяют направление вектора).
Если вектор 
, то направляющие косинусы этого вектора могут быть найдены по формулам:
, 
, 
.
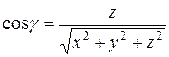Для них верно соотношение
.
Проекцией вектора на ось называется длина отрезка, заключенного между проекциями концов, взятая со знаком плюс, если направление вектора, соединяющего проекции концов, совпадает с направлением оси и со знаком минус в противном случае.
Вопрос 16. Скалярное произведение векторов. Определение, свойства, приложения. Скалярное произведение в координатной форме.
Скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
Скалярное произведение векторов 
и 
будем обозначать как 
. Тогда формула для вычисления скалярного произведения имеет вид 
, где 
и 
- длины векторов и соответственно, а 
- угол между векторами и .
Свойства скалярного произведения
1.скалярное произведение обладает переместительным свойством: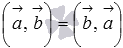 
2.скалярное произведение обладает сочетательным свойством относительно скалярного множителя: 
или 
, где 
- произвольное действительное число;
3. скалярное произведение обладает распределительным свойством:
4.скалярный квадрат вектора равен квадрату его длины:
5.если векторы и (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т.е. если 
Выражение скалярного произведения через координаты.
Пусть даны два вектора 
Найдем скалярное произведение векторов, перемножая их как многочлены (что законно в силу свойств линейности скалярного произведения) и пользуясь таблицей скалярного произведения векторов
т.е.
Итак, скалярное произведение векторов равно сумме произведений их одноименных координат.
Применения скалярного произведения
1. Определение угла между ненулевыми векторами
2.Нахождение проекции одного вектора на направление другого:
3. Нахождение работы постоянной силы
Вопрос 18.смешанное произведение векторов. Определение, свойства, приложения. Смешанное произведение в координатной форме.
Вопрос19. Различные виды уравнения прямой в R2. (общее, каноническое, параметрическое, с угловым коэффициентом.)
1. Общее уравнение прямой:
A x + B y + C = 0
где A и B не могут быть одновременно равны нулю.
2.Каноническое уравнение прямой:
Если известны координаты точки A(x0, y0) лежащей на прямой и направляющего вектора n = {l; m}, то уравнение прямой можно записать в каноническом виде, используя следующую формулу
| x- x0 | = | y - y0 |
| l | m |
3.Параметрическое уравнение прямой
Параметрические уравнения прямой могут быть записаны следующим образом
| x = l t+ x0 |
| y= m t+ y0 |
где (x0, y0) - координаты точки лежащей на прямой,
{l, m} - координаты направляющего вектора прямой.
4. Уравнение прямой с угловым коэффициентом
Общее уравнение прямой при B≠0 можно привести к виду
y = k x +b
где k - угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ
Вопрос 20. Нормированное уравнение прямой. Отклонение точки от прямой в R2.
Выведем нормальное уравнение прямой.
Пусть на плоскости зафиксирована прямоугольная декартова система координат Oxy. Зададим прямую в этой системе координат, указав точку, через которую она проходит, и нормальный вектор прямой. В качестве нормального вектора нашей прямой возьмем вектор единичной длины 
, с началом в точке O. Его координаты равны соответственно 
и 
, где 
и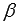 
- углы между вектором и положительными направлениями координатных осей Ox и Oy соответственно, то есть, 
. В качестве точки, через которую проходит прямая, возьмем точку А и будем считать, что она находится на расстоянии p единиц (
) от точки O в положительном направлении вектора (при p = 0 точка А совпадает с началом координат), то есть, 
.
Получим уравнение, которое задает эту прямую линию.
Очевидно, что точка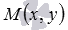 
лежит на рассматриваемой прямой тогда и только тогда, когда числовая проекция вектора 
на направление вектора равна p, то есть, при условии 
.
- радиус-вектор точки 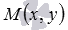, следовательно, 
, что было показано в разделе координаты радиус-вектора точки. Тогда из определения скалярного произведения векторов мы получаем равенство 
, а это же скалярное произведение в координатной форме имеет вид 
. Следовательно, 
или 
. На этом вывод нормального уравнения прямой закончен.
Полученное уравнение вида называют нормальным уравнением прямой или нормированным уравнением прямой, также называют уравнением прямой в нормальном виде
Отклонение точки от прямой 
или 
где знак перед корнем противоположен знаку C, если 
и выбран произвольно, если C = 0.
Билет 21
1.Прямые заданы общими уравнениямиПусть две прямые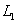 
и 
заданы общими уравнениями
и 
.
угол между прямыми, заданными общими уравнениями
.
Прямые заданы каноническими уравнениями
Пусть две прямые 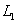и заданы каноническими уравнениями
и 
.
угол между прямыми, заданными каноническими уравнениями
. (2)
Прямые заданы уравненями с угловым коэффициентом
Пусть две прямые 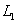и заданы уравнениями с угловым коэффициентом
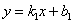и 
.
.
2.Если прямые заданы уравнениями с угловыми коэффициентами
и 
то для того, чтобы прямые были параллельны, необходимо и достаточно, чтобы
перпендикулярны, необходимо и достаточно, чтобы
если прямые заданы общими уравнениями
и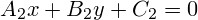 
то для того, чтобы прямые были параллельны, необходимо и достаточно, чтобы
перпендикулярны, необходимо и достаточно, чтобы
Если прямые заданы каноническими уравнениями 
Если 
, то прямые перпендикулярны.
Если 
, то прямые параллельны.
БИЛЕТ 22
1.Аналитическая геометрия - раздел геометрии, в котором геометрические фигуры и их свойства исследуются средствами элементарной алгебры на основе метода координат. В основе этого метода лежит так называемый метод координат, впервые применённый Декартом. Каждому геометрическому соотношению этот метод ставит в соответствие некоторое уравнение, связывающее координаты фигуры или тела.
Методы аналитической геометрии применимы к фигурам на плоскости, к поверхностям в трехмерном пространстве, а также допускают обобщение на пространства более высоких размерностей.
2. пространство, имеющее число измерений (Размерность)более трёх. Обычное евклидово пространство, изучаемое в элементарной геометрии, трёхмерно; плоскости— двумерны, прямые — одномерны. Возникновение понятия М. п. связано с процессом обобщения самогопредмета геометрии. В основе этого процесса лежит открытие отношений и форм, сходных спространственными, для многочисленных классов математических объектов (зачастую не имеющихгеометрического характера). В ходе этого процесса постепенно выкристаллизовалась идея абстрактногоматематического пространства как системы элементов любой природы, междукоторыми установлены отношения, сходные с теми или иными важными отношениями между точкамиобычного пространства.
Билет 23 Плоскость- поверхность, имеющая два измерения.(алгебраическая поверхность 1 порядка)
Общее уравнение плоскости:
Коэффициенты 
являются координатами нормального вектора плоскости
Уравнение плоскости в отрезках
где a, b, c - величины отрезков, отсекаемых плоскостью на осях координат.Нормальное уравнение плоскости 
где 
- углы, образуемые нормальным вектором плоскости с осями координат; p - расстояние от начала координат до плоскости.Уравнение плоскости проходящей через точку (х0,у0,z0) перпендикулярно данному вектору n(A, B, C)
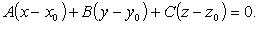
n- нормальный вектор к плоскости
Уравнение плоскости по трем точкам
Условие перпендикулярности двух плоскостей
или 
Условие параллельности двух плоскостей
Билет 24
Нормальным уравнением плоскости называется ее уравнение, написанное в виде
, (1)
где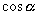 
, 
, 
- направляющие косинусы нормали плоскоти, p - расстояние от начала координат до плоскости. При вычислении направляющих косинусов нормали следует считать, что она направлена от начала координат к плоскости (если же плоскость проходит через начало координат, то выбор положительного направления нормали безразличен). Общее уравнение плоскости
приводится к нормальному виду (1) умножением на нормирущий множитель, определяемый формулой
;
знак нормирующего множителя берется противоположным знаку свободного члена нормируемого уравнения.Если точка 
имеет координаты 
, 
, 
, а плоскость задана нормальным уравнением
,то отклонение точки от этой плоскости дается формулой
Билет 25 Положение прямой в пространстве определено, если задать т. M0 и вектор S, параллельный этой прямой – направляющий вектор.
прямая в пространстве в прямоугольной системе координат Oxyz может быть задана:
системой из уравнений двух пересекающихся плоскостей 
|
|
|
