Параметрическое уравнение прямой

Если известна точка , принадлежащая прямой, и направляющий вектор данной прямой, то параметрические уравнения этой прямой задаются системой:

Канонические уравнения прямой

Если известна некоторая точка пространства , принадлежащая прямой, и направляющий вектор данной прямой, то канонические уравнения этой прямой выражаются формулами:

Уравнение прямой, проходящей через две заданные точки

Если известны две точки пространства , то уравнения прямой, проходящей через данные точки, выражаются формулами:

Условие параллельности двух прямых

5. Условие перпендикулярности двух прямых

mm ₁ + nn ₁ + pp ₁ = 0

(m,n,p) – координаты направляющего вектора

Прямая и плоскость параллельны:

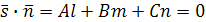
- направляющий вектор прямой

- нормальный вектор плоскости

Перпендикулярны:

Вопрос 26

Полярная система координат- двухмерная система координат, в которой каждая точка на плоскости определяется 2 числами-полярным углом и полярным радиусом. Полярная система координат особенно полезно в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространенной, декартовой или прямоугольной системе координат,такие отношения можно установить только путем применения тригонометрических уравнений. Переход от полярных координат к декартовым и обратно.Если полярную и декартову системы совместить так, чтобы начала их координат совпадали а полярная ось совпадала с положительным направлением оси абсцисс прямоугольной системы, то независимо от расположения точки В на плоскости получим формулу перехода от полярных координат r, a к декартовым х, у:

x=r cos a y=r sin a

и от декартовых к полярным:

r= tg a=

Вопрос 27

Преобразование декартовых координат при параллельном сдвиге осей определяется формулами:

x= +a y= +a

Здесь х, у-координаты произвольной точки М плоскости относительно старых осей, , -координаты той же точки относительно новых осей, a, b –координаты нового начала относительно старых осей (говорят так де, что а- величина сдвига в направлении абсцисс, b- величина сдвига в направлении оси ординат).

Преобразование декартовых прямоугольных координат при повороте осей на угол (который надо понимать, как в тригонометрии) определяется формулами:

х= cos a - sin a y= sin a + cos a

Вопрос 28

Общим уравнением второго порядка называется уравнение вида:

Ax²+2Bxy+Cy²+2Dx+2Ey+F=0

Коэффициенты уравнения A, B, C … действительные числ A²+B²+C² 0

Кривые второго порядка получаются в результате пересечения кругового конуса с плоскостями не проходящими через его вершину.

Если такая плоскость пересекает все образующие одной плоскости,то в сечении получается эллипс.

При пересечении образующих двух плоскостей образуется гипербола.

При пересечении какой-либо образующей получается парабола.

Эллипсом называется множество всех точек плоскости сумма расстояний от каждой из которых до двух данных точек этой плоскости (фокусы) есть величина постоянная равная 2А больше чем расстояние между фокусами.

+ =1

а и b – полуоси

Если центр эллипса совпадает с началом координат,то уравнение принимает вид:

+ =1

Свойства:

*Эллипс пересекает каждую из осей координат в двух точках.

*Сумма расстояний от любой точки эллипса до его фокусов есть величина постоянная и равная удвоенной большей полуоси.

*Эллипс имеет две взаимно перпендикулярные оси симметрии.

* Эллипс имеет центр симметрии.

*Эллипс может быть получен сжатием окружности.

Вопрос 29

Гиперболой называется множество точек плоскостей модуль разности от каждой из которой до 2 точек заданных в плоскости есть величина постоянная меньше чем расстояние между фокусом.

Каноническое ур-ние гиперболы:

- =1

Если центр совпадает с началом координат,то уравнение принимает вид:

- =1

Свойства:

*Гипербола не имеет общих точек с осью Oy, а ось Ox пересекает в двух точках A (a; 0) и B (–a; 0), которые называются вершинами гиперболы.

* Гипербола имеет две взаимно перпендикулярные оси симметрии.

* Гипербола имеет центр симметрии.

*Центр симметрии гиперболы называют центром гиперболы.

*Гипербола пересекается с прямой y = kx при в двух точках. Если то общих точек у прямой и гиперболы нет.

Вопрос 30

Параболой называется множество всех точек плоскости в каждой из которых равноудалена от заданной точки этой же плоскости называемой фокусом и заданной прямой называемой директрисой.

Каноническое ур-ние параболы:

- =

Свойства параболы:

* Парабола имеет ось симметрии

* Парабола расположена в полуплоскости x ≥ 0

Вопрос №31

Поверхности второго порядка

Поверхность второго порядка - геометрическое место точек трёхмерного пространства, прямоугольные координаты которых удовлетворяют уравнению

в котором по крайней мере один из коэффициентов , , , , , отличен от нуля.

Цилиндрические поверхности.

Поверхность S называется цилиндрической поверхностью с образующей 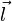, если для любой точки M₀ этой поверхности прямая, проходящая через эту точку параллельно образующей 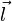,целиком принадлежит поверхности S.

Коническая поверхность.

Поверхность S называется конической поверхностью с вершиной в точке O, если для любой точки M₀ этой поверхности прямая, проходящая через M₀ и O, целиком принадлежит этой поверхности.

Поверхности вращения.

Поверхность S называется поверхностью вращения вокруг оси OZ, если для любой точки M₀(x₀,y₀,z₀)поверхности окружность, проходящая через эту точку в плоскости z=z₀ с центром (0,0,z₀) и радиусом целиком принадлежит этой поверхности.

Эллиптический параболоид. Уравнение эллиптического параболоида имеет вид

Гиперболический параболоид. Уравнение гиперболического параболоида имеет вид

Центральные поверхности.

Если центр поверхности второго порядка существует и единственен, то его координаты (x₀,y₀,z₀) можно найти решив систему уравнений

Вопрос №32

Множество – одно из ключевых понятий математики, в частности, теории множеств и логики. Понятие множества обычно принимается за одно из исходных (аксиоматических) понятий, то есть не сводимое к другим понятиям, а значит, и не имеющее определения. Формулировка Бертрана: Множество есть совокупность различных элементов, мыслимая как единое целое.

Бинарные операции:

1)пересечение:

.

2)объединение:

.

Если множества и не пересекаются, то . Их объединение обозначают также: .

3)разность:

.

4)симметрическая разность:

.

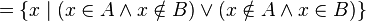5)декартово или прямое произведение:

.

Вопрос №33

Элементы теории функций.

Определение: Если каждому комплексному числу Z из некоторого множества D по некоторому закону поставлено в соответствие определенное комплексное число W из множества G, то на этой области задана однозначная функция комплексного переменного, отображающая множество D на множестве G. W= F(Z).

Множество D называется Областью определения, множество G – областью значений функции.

Комплексную функцию можно записать в виде:

U,V- действительные функции от переменных X и Y. Если каждому соответствует несколько различных значений W=F(Z) называется многозначной. Определение: функция имеет предел в точке Z0, равный числу А = a + ib, если

Элементарные функции- функции, которые можно получить с помощью конечного числа арифметических действий и композиций из следующих основных элементарных функций:

1) алгебраическая

2) степенная

3) рациональная

4) трансцендентные

5) показательная и логарифмическая

6) тригонометрическая и обратные тригонометрические

Вопрос №34

Числовая последовательность - это последовательность элементов числового пространства. Числовые последовательности являются одним из основных объектов рассмотрения в математическом анализе.

Пусть X – это либо множество вещественных чисел R, либо множество комплексных чисел C. Тогда последовательность элементов множества X называется числовой последовательностью.

Предел последовательности: Число называется пределом числовой последовательности , если последовательность является бесконечно малой, т.е все её элементы, начиная с некоторого. По модулю меньше любого заранее взятого положительного числа.

Число е: e-математическая константа, основание натурального логарифма, трансцендентное число. Иногда число е называют числом Эйлера или числом Непера. Обозначается строчной латинской буквой е и численно равно 2.7182

Вопрос №35

Бесконечно малая – числовая функция или последовательность, которая стремится к нулю.

Последовательность называется бесконечно малой, если Функция называется бесконечно малой в окрестности точки , если .

Функция называется бесконечно малой на бесконечности, если либо .

Теорема о бесконечно малых. Если функция y=f(x) представима при x→aв виде суммы постоянного числа b и бесконечно малой величины α(x): f (x)=b+ α(x) то .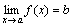

Обратно, если 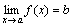, то f (x)=b+α(x), где a(x) – бесконечно малая при x→a.

Сравнение бесконечно малых. Пусть а(x), b(x) и g(x) – бесконечно малые функции при. Будем обозначать эти функции a,b,g соответственно. Эти бесконечно малые функции можно сравнивать по быстроте их убывания, т.е по быстроте их стремления к нулю.

Бесконечно большая – числовая функция или последовательность. Которая стремится к бесконечности определенного знака.

Последовательность называется бесконечно большой, если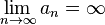

Функция называется бесконечно большой в окрестности точки , если .

Функция называется бесконечно большой на бесконечности, если либо .

Теорема о связи между бесконечно большой и бесконечно малой функциями: Если функция - функция бесконечно малая (), то функция есть бесконечно большая функция и наоборот.

ВОПРОС №:36

ПРЕДЕЛ ФУЕКЦИИИ В ТОЧКЕ

Пусть функ. Y=f(x) определена в некоторой окрестности х0, кроме самой точки х0.Число А называется пределом функ. В точке х0 или при х → х0 если для любого > 0

Найдется >0 такое что для всех

х ≠х0 для которых 0<| х-х0| < , выполняется неравенство

|f(x)-A|<

Запись

LIM f(x) = A

x→x0

ОДНОСТОРОННИЕ ПРЕДЕЛЫ

Пределы функ. Слева или справа наз. Односторонними

Число A1. Называется пределом функ y=f(x) слева, если для любого > 0 существуют

= ()>0 такое что при х принадлежащему промежутку

(х0- ;x0) выполняется неравенство |f(x)-A1|<

запись

LIM f(x) = A1

X→x0-0

Предел справа – аналогично

запись

LIM f(x) = A2

X→x0+0

Основные теоремы о пределах

Пусть даны ф f(x) и g(x) и X→0

1)Педел суммы 2-х функ. = сумме(разности)их пределов

LIM(f(x) ± g(x)) = lim f(x) ± lim g(x)

X→0

2)Lim произведения 2-х функ.=произв. Их пределов

LIM(f(x)* g(x)) = lim f(x) *lim g(x)

X→ 0

3)lim дрорби =lim числителя на lim знаменателя

Limf(x)/g(x) =lim Limf(x)/lim g(x)

X→ 0

Замечания: 1)функ. Может иметь один предел при х→х0

2)Постоянное множество можно выносить за знак lim

3) lim степени с натуральным показателем равен той же степени предела

Виды неопределенностей

1)[0\0] Раскрытие- числитель и знаменатель делим на (х-а) а – то к чему стремится

2)[ ∞\ ∞] Раскрытие- числит и знам делим на х^n n- наибольший показатель

3)[1^∞] Раскрытие – подводим ко 2-му замечательному пределу.

При неопределенностях другого вида с помощью преобразований приводим к 1 из 3 видов

Вопрос 37

Непрерывность ф.

Ф. f(x) называется непрерывной в х0,если она определена в некоторой окрестности точки,

существует предел f(x) в точке Х0,

это предел равен значению функции в точке х0

lim f(x)=f(x0)

X→x0

Классификация точек разрыва

1) точка х0 называется точкой разрыва функ. f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке

2)точка х0 называется точкой разрыва 1-го рода,если в этой точке функ. f(x) имеет конечные, но не равные друг другу левый и правый пределы

3) точка х0 называется точкой разрыва 2-го рода,если в этой точке функ. f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен

ТЕОРЕМЫ

1)Пусть заданы две функцииf(x) и g(x), непрерывные на некотором множестве X. Сумма, произведение и частное (при условии, что g(x) ≠0) является также непрерывной функцией на рассматриваемом множестве.

2) Пусть функцияy= ɸ(x) непрерывна в точке a, а функция u=f(y) непрерывна в точке b=ɸ(a). Тогда композиция(сложная функ) этих функций u=f(ɸ(x)) непрерывна в точке a.

3) Если функция f(x) является непрерывной и строго монотонной на отрезке[a;b], которые лежит на оси абсцисс, то и обратная функция y=g(x) также непрерывна и монотонна на некотором отрезке[c;d] оси ординат.

4)Каждая элементарная функция, заданная в окрестности некоторой точки, непрерывна в этой точке.

Вопрос 38

Первый замечательный предел

Lim sinx\x=1

X→0

Применяется при неопр [0\0]

И наличии тригонометрич ф.

Верно и обратное

Lim x\sinx=1

Второй замечательный предел

Lim(1+1\x)^x=e

X→∞

Применяется в неопр [1^∞]

В более общем виде этот предел имеет вид lim(1+k\x)^x\k =e

X→∞

В качестве параметра может выступать не только переменная х, но и функ.

Замечание

1/х=t, t→0, то верно

Lim(1+t)^1\t=e

t→0

Вопрос 39

Приращение функц

Приращение функции – разность между двумя значениями функции.

1. Функция одной переменной. Пусть задана функция у = f(x), определенная при значении аргумента, равном х0. Дадим аргументу приращение Dх, т.е. рассмотрим значение аргумента, равное x0 + Dх. Предположим, что это значение аргумента также входит в область определения данной функции. Тогда разность

Dy = f(x0 + Dх) – f(x0) называется приращением функции.

2. Функция многих переменных. Пусть в некоторой области D n-мерного пространства задана функция z = f(x1; x2; …; xn) и пусть точки М и N принадлежат области D – входят в область определения данной функции. При переходе из точки M в точку N каждая координата хi точки получит приращение Dхi, i = 1, 2, …, n, а данная функция – приращение Dz = f(N) – f(M) = f(x1+Dx1; x2+Dx2; …; xn+Dxn) – f(x1;x2; …; xn). Это приращение называют иногда полным, в отличие от частного приращения Di z, при котором получает приращение только аргумент хi, а все остальные аргументы сохраняют первоначальное значение: Di z = f(x1, x2, …; xi–1; xi+1; …; xn) – f(x1; x2; …; xn).

Приращение аргумента

Приращение аргумента – разность между двумя значениями аргумента («новым» и «старым»). Обычно обозначается через Dх: Dх = x1 – x0

Понятие производной

Предел отношения приращения функ dy(d-дельта) в этой точке(если он существует) и приращения аргумента dy,когда dx→0 называется производной функ f(x) в точке х0

Y^|=lim(f(x0+dx)-f(x0)\dx)

dx→0

f^|(x0)= lim(f(x)-f(x0)\x-x0)

x→x0

Геометрический и механический смысл.

Рассмотрим график функции y = f (x):

Из рис видно, что для любых двух точек A и B графика функции: где а - угол наклона секущей AB.Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точку B, то dx неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. В этом и состоит геометрический смысл производной. Уравнение касательной. Выведем уравнение касательной к графику функции в точке A (x0, f (x0)). В общем случае уравнение прямой с угловым коэффициентом f ’(x0) имеет вид: y = f ’(x0) · x + b.Чтобы найти b, воспользуемся тем, что касательная проходит через точку A:

f (x0) = f ’(x0) · x0 + b,

отсюда, b = f (x0) – f ’(x0) · x0, и подставляя это выражение вместо b, мы получим уравнение касательной:y = f (x0) + f ’(x0) · (x – x0).Механический смысл производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан: координата x движущейся точки – известная функция x (t) времени t. В течение интервала времени от t0 до t0 + dt точка перемещается на расстояние: x (t0 +) - x (t0) = dt, а её средняя скорость равна: v =dx/dt. При dt → 0 значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью v (t0) материальной точки в момент времени t0. Но по определению производной мы имеем:lim(dx\dt)=lim (x(t0+dt)-

x0(t)\dt)=x^|(t0)

dt→0отсюда, v (t0) = x’ (t0), т.e. скорость – это производная координаты по времени. В этом и состоит механический смысл производной. Аналогично, ускорение – это производная скорости по времени: a = v’ (t).

Вопрос40 Дифференцируемость функ. Ф y=f(x) имеющая производную в каждой точке интервала (a;b) наз дифференцируемой в этом интервалеОперация нахождения производной наз дифференцирование Связь между диф. И непрерывностью. Если функ y=f(x) диф в точке х,то она и непрерывна в этой точке,обратное не гарантируемо

Вопрос 41. Производная неявной функции и параметрически заданной
Говорят, что уравнение задает неявно функцию , на интервале , если для всех выполняется равенство .

Для вычисления производной функции 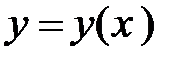следует продифференцировать по тождество 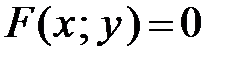, помня, что есть функция от x, а затем полученное уравнение разрешить относительно .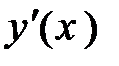

Пример 3.1.Найти значение в точке 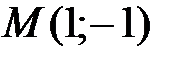для функции, заданной неявно уравнением .

Решение. Дифференцируя по x обе части данного уравнения и считая при этом функцией от x, получаем:

,

откуда .

Полагая x = 1, y = –1, находим

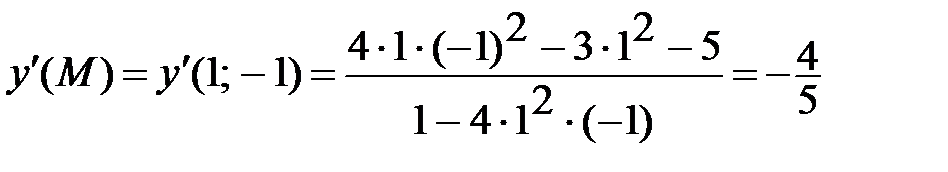
Предположим, что функциональная зависимость от не задана непосредственно , а через промежуточную величину — . Тогда формулы

задают параметрическое представление функции одной переменной.

Пусть функция задана в параметрической форме, то есть в виде:

где функции и определены и непрерывны на некотором интервале изменения параметра . Найдем дифференциалы от правых и левых частей каждого из равенств:

Далее, разделив второе уравнение на первое, и с учетом того, что , получим выражение для первой производной функции, заданной параметрически:

Для нахождения второй производной выполним следующие преобразования:

Задание. Найти вторую производную для функции заданной параметрически.

Решение. Вначале находим первую производную по формуле:

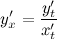
Производная функции по переменной равна:

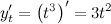
производная по :

Тогда

Вторая производная равна

вопрос 42. Логарифмическое дифференцирование.

Для функций вида для упрощения нахождения производной рациональнее использовать логарифмическое дифференцирование.

Суть метода логарифмического дифференцирования

Суть такого дифференцирования заключается в следующем: вначале находится логарифм заданной функции, а уже затем вычисляется от него производная. Пусть задана некоторая функция . Прологарифмируем левую и правую части данного выражения:

Далее продифференцируем полученное равенство при условии, что является функцией от , то есть найдем производную сложной функции:

А тогда, выражая искомую производную , в результате имеем:

Задание. Найти производную функции

Решение. Если находить производную данной функции, используя таблицу производных и правила дифференцирования, то процесс будет очень трудоемким. Производную будем находить с помощью логарифмического дифференцирования. Прологарифмируем левую и правую части заданной функции:

Используя свойства логарифмов, преобразуем правую часть полученного равенства к следующему виду:

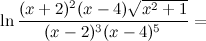
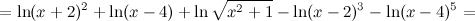
Таким образом, получаем, что логарифм заданной функции равен:

Дифференцируем левую и правую часть последнего равенства, не забывая, что является функцией переменной :

Итак,

Отсюда

Подставляя вместо функции ее выражение, окончательно будем иметь, что

Вопрос 43. Производные высших порядков

Пусть функция y = f (x) определена на множестве D и существует . Тогда на D определена функция . Если эта функция имеет производную в точке x Î D, то её называют производной второго порядка (или второй производной) функции f (x) в точке x.

Обозначается , , , .

Таким образом .

Производные высших порядков определяются индуктивно. Если для любого существует , то на D определена функция . Производная от этой функции (если она существует) в точке x Î D называется производной n–го порядка функции f (x) в точке x.

.

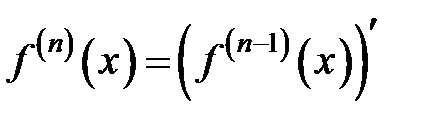Обозначается: , , , .

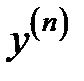Cчитают, что .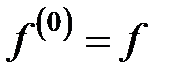

Заметим, что если существует в точке х, то в некоторой окрестности точки существует и все производные более низкого порядка k, k < n..
Вопрос44. Дифференциал функции. Его геометрический смысл. Использование дифференциала в приближенных вычислениях.

Пусть функция f (x) дифференцируема в точке х ₀. Дифференциалом функции f (x) в точке х ₀ называется главная часть приращения функции, линейно зависящая от приращения аргумента . Обозначается dy, . Таким образом, согласно определению

.

Рассмотрим функцию , , то есть для независимого аргумента х дифференциал и приращение совпадают: .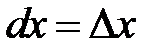

Дифференциалом независимой переменной х называется ее приращение : .

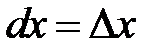Тогда из определения дифференциала следует

.

Из определения производной и дифференциала следует, что при малых справедливо приближенное равенство: или формула:

(5)

Пример. Вычислить приближенно: .

Решение. Для приближенного вычисления будем использовать формулу (5).

В нашем случае следует взять , , . Выберем и так, чтобы вычислялось легко, а было достаточно мало по модулю: , .

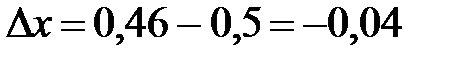Подставим эти значения в формулу (5):

Ответ: .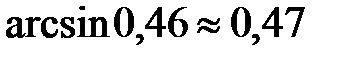

Пример. Вычислить приближенно .

Решение. Для приближенного вычисления будем использовать формулу (5)

В нашем случае следует взять , , . Выберем и так, чтобы вычислялось легко, а было достаточно мало по модулю: , .

Подставим эти значения в формулу (5):

.

Ответ: .

вопрос 45. Основные теоремы дифференциального исчисления (т. Ферма, т. Ролля, т. Лагранжа)

Пусть функция определена и дифференцируема на интервале (а,в) и в некоторой точке принимает наибольшее или наименьшее значение. Тогда 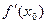=0.

Док-во. Пусть 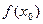- наибольшее значение функции на интервале (а,в). Тогда при : , .

При 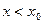: , .Если функция по условию дифференцируема в т. , то указанные выше пределы должны совпадать. А это возможно лишь при 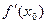=0.▲

Геометрически теорема Ферма означает, что в точках наибольшего или наименьшего значений дифференцируемой функции касательная к графику функции имеет нулевой угловой коэффициент, т.е. параллельна оси Ох.

Теорема Ролля (о среднем).Пусть функция :

1) непрерывна на отрезке ;

2) дифференцируема на интервале ;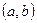

3) принимает на концах интервала равные значения: f(a)=f(b).

Тогда существует т. , такая, что