Причинно-следственная диаграмма

Причинно-следственная диаграмма (диаграмма Исикавы) – инструмент, позволяющий в упорядоченном виде представить все факторы, влияющие на конечный результат, и помогающий выявить основные факторы, влияющие на конечный результат.

Причинно-следственная диаграмма часто называется также диаграммой Исикавы (по имени ее автора), диаграммой «причина-следствие», «рыбьей костью», «рыбьим скелетом». Она позволяет выявить и систематизировать различные факторы и условия, оказывающие влияние на рассматриваемую проблему (на показатели качества, такие как простои автомобилей по техническим неисправностям, наработка на отказ и т. д.). Информация о показателях качества для построения диаграммы собирается из всех доступных источников. При построении диаграммы выбираются важные с технической точки зрения факторы.

Сложная причинно-следственная диаграмма анализируется с помощью расслоения по отдельным факторам. При выявленной анализом заметной разнице в разбросе между «слоями» принимают соответствующие меры для ликвидации этой разницы и устранения причины ее появления.

При использовании причинно-следственной диаграммы процесс производства рассматривают как взаимодействие 4М (material – (материал) + machine – (оборудование) + man – (оператор)+method – (метод)). Зависимость между процессом, представляющим собой систему причинных факторов, и качеством, представляющим собой результат действия этих причинных факторов, можно выразить графически, как показано на рис. 1.10.

 

 

Рис. 1.10. Причинно-следственная диаграмма

 

 

Если результат процесса оказался неудовлетворительным, то в системе причин, т. е. в какой-то точке процесса, произошло отклонение от заданных условий. Если постоянно поддерживать заданные условия хода процесса, можно обеспечить формирование высокого качества.

Как показано на рис. 1.10, характеристики качества, являющиеся следствием, определяют причины М1–М4, обозначенные стрелками. Эти причины являются, в свою очередь, следствием других причин. Все они также обозначены стрелками, направленными к соответствующим следствиям. Вторичным причинам могут соответствовать третичные причины и т. д.

Для составления причинно-следственной диаграммы необходимо подобрать максимальное количество факторов, имеющих отношение к характеристике, которая вышла за пределы допустимых значений.

Наиболее эффективным считается групповой метод анализа причин, называемый «мозговым штурмом». В этом случае, если проблема возникла на участке, к группе экспертов присоединяются лица, непосредственно работающие на этом производственном участке.

При анализе причин часто приходится пользоваться другими статистическими методами и прежде всего – методом расслоения.

 

Диаграммы разброса

Диаграмма разброса – инструмент, позволяющий определить вид и тесноту связи между парами рассматриваемых переменных.

Диаграмма разброса используется для выявления зависимости между показателями качества (результат) и основными факторами производства (причина) при анализе причинно-следственной диаграммы или для выявления корреляционной зависимости между факторами.

Диаграмма разброса, так же как и метод расслоения, используется для выявления причинно-следственных связей показателей качества и влияющих факторов при анализе причинно-следственной диаграммы.

При наличии корреляционной зависимости причинный фактор оказывает очень большое влияние на характеристику процесса, поэтому, удерживая этот фактор под контролем, можно достичь стабильности характеристики.

При такой зависимости между отдельными факторами значительно облегчается контроль процесса с технологической, временной и экономической точек зрения.

Для построения диаграммы разброса прежде всего, проводят сбор этих данных и представляют их в виде таблицы соответствия тех и других какому-то общему для них условию сбора.

Если данных мало, четкую зависимость установить трудно, поэтому желательно, чтобы число пар было не менее 30. Однако даже в тех случаях, когда число данных оказывается всего лишь порядка 10, часто можно получить какую-то полезную информацию.

Существуют различные методы оценки степени корреляционной зависимости. Одним из них является метод вычисления коэффициента корреляции по формуле

 

,

 

где х_i, у_i – значения параметров х и у для i -го измерения; х, у – средние арифметические значения величин х и у; S_x, S_y — стандартные отклонения величин х и у; п – число измерений в выборке (объем выборки).

Если r = ±1, это свидетельствует о наличии корреляционной зависимости, если r = 0, корреляционная зависимость отсутствует. Чем ближе коэффициент корреляции к 1, тем теснее зависимость между параметрами.

Эффективным и более простым методом анализа степени корреляционной зависимости считается метод медиан, удобный при исследовании технологического процесса с использованием данных, полученных на рабочем месте.

Диаграмма разброса строится как график зависимости между двумя переменными и .

Применяют две разновидности метода медиан. Рассмотрим действие первого метода на практическом примере, диаграмма разброса для которого приведена на рис. 1.11.

Рис. 1.11.. Диаграмма разброса для определения зависимости между 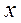и методом медиан

 

На график наносятся данные в порядке измерений. Если на одну и ту же точку графика попадает два или три значения, они обозначаются как точка в круге, или в двух кругах, или возле точки проставляется число данных, или рядом с нанесенной точкой сразу перед ней ставятся еще одна, две точки и т. д.

На диаграмме разброса проводятся вертикальная и горизонтальная линии медиан. Выше и ниже горизонтальной медианы, справа и слева от вертикальной медианы должно быть равное количество точек.

Если количество точек окажется нечетным, следует провести линию через центральную точку. В каждом из четырех квадрантов, получившихся в результате разделения диаграммы разброса вертикальной и горизонтальной медианами, подсчитывают число точек и обозначают соответственно. Точки, через которые прошла медиана, не учитывают. Отдельно складывают число точек в положительных и отрицательных квадрантах и их общую сумму:

 

;

;

.

 

Для определения наличия и степени корреляции по методу медиан используется специальная таблица (табл. 1.2) кодовых значений, соответствующих различным при двух значениях коэффициента риска 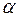(0,01 и 0,05). Сравнивают меньшее из чисел и с кодовым значением, соответствующем значению , делают заключение о наличии и характере корреляции. Если меньшее из чисел и оказывается равным или меньше табличного кодового значения, то корреляционная зависимость имеет место.

В соответствии с данными таблицы для = 25 (числа степеней свободы) и значении коэффициента риска = 0,01 кодовое значение меньшего из чисел и равно 5. Поскольку полученное в результате расчетов число 5 не превышает табличное значение, можно утверждать, что между двумя параметрами существует корреляционная зависимость с коэффициентом риска, равным 0,01. При этом, так как > 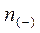это свидетельствует о прямой корреляции. В противном случае можно было говорить об обратной корреляции.

На рис. 1.12 приведен пример использования второй разновидности метода медиан.

Рис. 1.12. Анализ корреляции между переменными и с помощью метода медианы: 1 – график ; 2 – график ; 3 – линия медианы

x·y: = 11 + 4/2 = 13;

x·y: = 14 + 4/2 = 16;

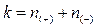= 13 + 16 = 29.

 

Таблица 1.2

 

Таблица кодовых значений (извлечения)

 

k		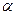k		k
0,01	0,05	0,01	0,05	0,01	0,05

 

 

В соответствии с данными таблицы для =29 (числа степеней свободы) и значении коэффициента риска =0,05 кодовое значение для меньшего из чисел и 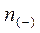равно 8. Поскольку полученное в результате расчетов число 13 превышает табличное значение 8, можно утверждать, что между двумя параметрами не существует корреляционная зависимость с коэффициентом риска, равном 0,05.

 

 

Контрольные карты

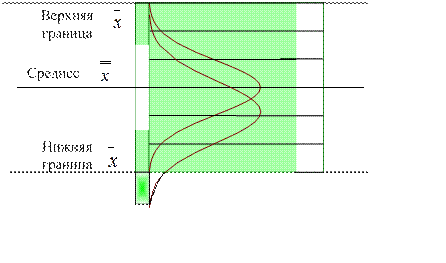
Контрольная карта – инструмент, позволяющий отслеживать ход протекания рассматриваемого процесса и воздействовать на него с целью предупреждения отклонения от требуемых значений.

Контрольные карты, как инструмент управления качеством, предложены У. Шухартом в 1924 г.

Контрольная карта – это разновидность графика, однако она отличается от обычного графика наличием линий, называемых контрольными границами или границами регулирования. Эти контрольные границы обозначают ширину разброса, образующегося в обычных условиях течения процесса. Если все точки на графике входят в область, ограниченную контрольными границами, это указывает на то, что процесс протекает в относительно постоянных условиях, т. е. указывает на стабильность процесса. И наоборот, точки, выходящие за пределы контрольных границ, означают, что в ходе процесса возникли погрешности, нарушившие стабильность процесса.

Контрольная карта представляет собой специальный бланк, на котором проводятся центральная линия и две линии выше и ниже средней, называемые верхней и нижней контрольными границами. На карту точками наносятся данные измерений или контроля параметров. Записывают условия производства.

Исследуя изменение данных с течением времени, следят, чтобы точки графика не вышли за контрольные границы. В случае отклонений выясняют причины с использованием других инструментов контроля качества.

В производственной практике применяются следующие виды контрольных карт:

● карта средних арифметических и размахов () – применяется в случае контроля по количественному признаку таких показателей качества, как длина, масса, прочность на разрыв и др.;

● карта индивидуальных значений (х) – применяется в случае необходимости быстрого обнаружения незамеченных факторов или в случае, когда за день или за неделю было произведено только одно наблюдение;

● карта доли дефектной продукции (р) – применяется в случае контроля качества по определению доли дефектных изделий (например, доли дефектных винтов по длине винта, доли дефектных электрических лампочек по качеству металла и т. д.);

● карта числа дефектных единиц продукции (pn) – применяется в случае контроля качества по определению числа дефектных изделий;

● карта числа дефектов (С) – применяется в случае, когда контроль качества осуществляется путем определения суммарного числа дефектов в заранее установленном постоянном объеме проверяемых изделий (например, число разрывов на постоянной площади ткани);

● карта числа дефектов на единицу продукции (U) – применяется в случае контроля качества по числу дефектов на единицу продукции, когда площадь, длина или другой параметр образца продукции не являются постоянной величиной.

Данные, представляемые в контрольной карте используются для построения гистограмм. Графики, получаемые на контрольных картах, сравниваются с контрольными нормативами.

Представление полученных данных в виде графика в порядке их поступления в ходе технологического процесса в виде временного ряда позволяет оценить изменения, которые происходили на этот период. Таким образом, график отражает динамику процесса.

Разброс показателей качества в пределах считается допустимым. Такой разброс вызван случайными отклонениями показателей (качества исходных материалов или деталей, а также условий производства), и называется неизбежным разбросом (рассеянием) показателей качества. Неизбежный разброс показателей качества и не требует вмешательства в ход процесса.

Если же на графике часть точек выходит за пределы верхней или нижней контрольной границы, это значит, что показатели качества испытывают разброс, выходящий за пределы контрольных нормативов. Такой разброс называется устранимым разбросом (рассеиванием) показателей качества. Как только на контрольной карте появляется одна или несколько точек на графике, выходящих за пределы контрольного диапазона, необходимо немедленно принять все меры для выявления и устранения причины отклонения.

Эта карта составляется в следующем порядке:

1. Собирают предварительные данные измерений характеристик числом в пределах 100. Эти данные делятся на 4–5 групп, равных по количеству данных, так что в результате в каждой группе получается по 20–25 данных. (в примере 5 групп). Для регистрации и систематизации предварительных данных используют специальные бланки для контрольных листков, пример заполнения которых приведен во второй части данного пособия.

2. Находят средние значения 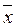и размах для каждой группы. Затем определяют среднее значение 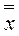и среднее значение 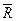. Эти средние значения определяют среднюю линию контрольного диапазона: 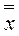– среднюю линию дли 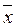-карты, 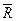– среднюю линию для R -карты.

Для рассматриваемого случая 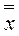=5,406; 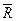=0,195.

 

Средняя линия обычно обозначается сплошной линией.

3. Устанавливают контрольные границы по выше приведенным выражениям.

 

 

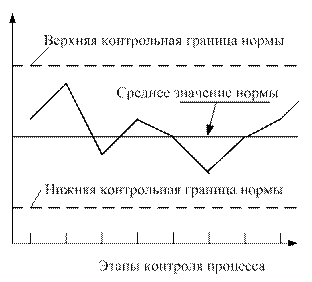
Рис. 1.13. Все точки находятся в пределах контрольных границ; процесс устойчив

 

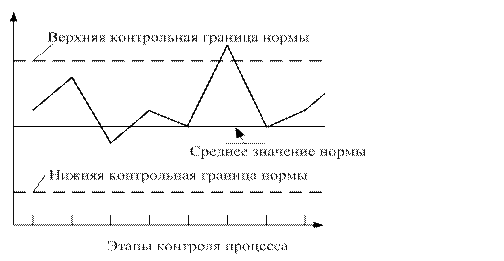
Рис 1.14. Наблюдается выброс точек за пределы контрольной границы

(возникновение отклонений процесса)

 

Рис. 1.15. За контрольную границу вышла точка на графике – изменилось среднее

Рис. 1.16. За контрольную границу вышли точки на графике – увеличился разброс

 

Для осуществления контроля процесса с помощью контрольных карт, прежде всего из показателей качества, формируемых в результате этого процесса, выбирают наиболее важные, которые сравнительно быстро могут быть представлены в виде количественных данных.

Когда процесс протекает стабильно и удовлетворяет всем требованиям с технологической и экономической стороны, говорят, что «процесс находится в контролируемом состоянии».

Если при построении контрольной карты окажется, что одна или несколько точек выходят за контрольные границы, это означает, что нарушены условия обеспечения одного или нескольких факторов, относящимся к исходным материалам или контролируемым параметрам.

В соответствии с принятыми правилами построения контрольных карт точка, расположенная точно на контрольной границе, считается вышедшей за пределы контрольной границы.

В том случае, когда при исследовании причины отклонения параметра, приведшего к выходу точки за контрольную границу, удается эту причину устранить, центральную линию и контрольные границы следует пересчитать, исключив данные для группы, относящейся к точке, вышедшей за контрольную границу (вновь рассчитать только по оставшимся данным).

 

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: