 |
ПРИМЕР 2. Найти значение выражения:
|
|
|
|

при с=2, d=1/4
Решение.
Определим переменные:


Вычислим:

Задания для самостоятельного выполнения.
Задание 1.  Вычислить.
Вычислить.
1) 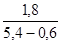 5)
5)  9)
9) 
2)  6)
6)  10)
10) 
3)  7)
7) 
4)  8)
8) 
Задание 2.
Найти значение выражения.
1  при a=4.8, b=1.2.
при a=4.8, b=1.2.
2.  при a=0.75, b=4/3.
при a=0.75, b=4/3.
3.  при a=1.2, b=3/5.
при a=1.2, b=3/5.
4. 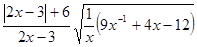 при x=-3.
при x=-3.
5.  при x=1, y=0.
при x=1, y=0.
6. 
 при х=-2.
при х=-2.
7.  при а=54, b=6.
при а=54, b=6.
8.  при
при  ,
, 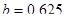 и c=3.2.
и c=3.2.
9. 
 при a=0.02, b=-11.05 и c=1.07
при a=0.02, b=-11.05 и c=1.07
10.  при
при  .
.
ЛАБОРАТОРНАЯ РАБОТА №2
Тема. Решение уравнений и их сиситем.
Цель. Научиться решать одно уравнение с одним неизвестным и системы уравнений в Mathcad.
Краткие сведения.
I. Решение одного уравнения с одним неизвестным.
Для решения одного уравнения с одним неизвестным используется функция ROOT. Аргументами этой функции является выражение и переменная, входящая в выражение. Ищется значение переменной, при котором выражение обращается в ноль. Функция возвращает значение переменной, которое обращает выражение в ноль.
Для определения корней уравнения необходимо привести уравнение к виду F (x)=0 и использовать функцию поиска корней следующим образом: root (F (x), x), где F(x) – заданное уравнение, x – переменная, относительно которой это уравнение решается. Для поиска корней Mathcad использует приближенные методы вычислений, поэтому перед использованием функции root необходимо задать начальное приближение для переменной, относительно которой решается уравнение.
ПРИМЕР 1. Найти а - решение уравнение уравнения  .
.
Решение.
Определим начальное значение переменной х:
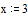
Определим выражение, которое должно быть обращено в ноль.Для этого перепишем уравнение  в виде
в виде 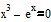 .
.
Левая часть этого выражения является вторым аргументом функции ROOT.
|
|
|
Определим переменную а как корень уравнения:

Найдем значение корня:

Помните! Начальное значение переменной должно быть присвоено до начала использования функции root.
II. Решение системы уравнений.
Для решения нескольких уравнений совместно Mathcad представляет блок решений. Блок решений состоит из ключевого слова Given, группы уравнений и заканчивается функцией Find.
Для решения системы уравнений необходимо сделать следующее:
Ø Задать начальные приближения для всех неизвестных, входящих в систему уравнений. Mathcad решает уравнения при помощи итерационных методов. На основе начального приближения строится последовательность, сходящаяся к искомому решению.
Ø Напечатать ключевое слово Given. Оно указывает Mathcad, что далее следует система уравнений.
Ø Ввести уравнения и неравенства в любом порядке ниже ключевого слова Given. Удостоверьтесь, что между левыми и правыми частями уравнений стоит символ «=». Используйте <ctrl>= для печати символа =. Между левыми и правыми частями неравенств может стоять любой из символов: <, >, ≤‚ ≥.
Ø Ввести любое выражение, которое включает функцию Find. Эта функция возвращает решение системы уравнений. Число аргументов должно быть равно числу неизвестных.
ПРИМЕР 2. Решить систему уравнений

Решение.
Определим начальные значения для всех переменных:


Введем систему уравнений после ключевого слова Given:



Зададим ограничения для переменных в виде неравенств:


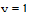
Введем выражение, которое включает функцию Find:

Найдем решение системы:

Задания для самостоятельного выполнения.
Задание 1. Решить уравнение.
1. x=cos(x) 6. 
2. 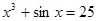 7.
7. 
3.  8.
8. 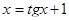
4.  9.
9. 
5.  10.
10. 
Задание 2. Решить систему уравнений.
1. 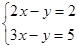 5.
5.  9.
9. 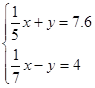
|
|
|
2.  6.
6. 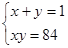 10.
10. 
3.  7.
7. 
4.  8.
8. 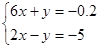
ЛАБОРАТОРНАЯ РАБОТА №3.
Тема. Дифференцирование функции. Геометрический смысл производной.
Цель. Научиться находить численное значение производной функции в заданной точке.
Краткие сведения.
I. Вычисление производной функции.
Оператор производной Mathcad предназначен для нахождения численного значения производной функции в заданной точке. Для вычисления производной используется клавиша со знаком?.
Для того, чтобы найти производную функции и вычислить ее численное значение, необходимо сделать следующее:
Ø Сначала определить точку, в которой необходимо найти производную.
Ø Щелкнуть ниже определения этой точки. Затем набрать?. Появится оператор производной с двумя полями: 
Ø Щелкнуть на поле в знаменателе и набрать имя переменной, по которой проводится дифференцирование.
Ø Щелкнуть на поле справа от  и набрать выражение, которое нужно дифференцировать.
и набрать выражение, которое нужно дифференцировать.
Ø Чтобы увидеть результат, нажать знак =.
ПРИМЕР 1. Найти производную  по
по 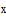 в точке
в точке 

Решение:
Определим точку, в которой необходимо найти производную:

Введем оператор производной, заполним поля и вычислим производную:
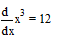
Помните!
Ø Результат дифференцирования есть не функция, а число – значение производной в указанной точке переменной дифференцирования.
Хотя дифференцирование возвращает только одно число, можно определить одну функцию как производную другой функции. Например: 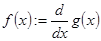 .
.
Вычисление f(x) будет возвращать в численной форме производную g(x) в точке х.
Выражение, которое нужно дифференцировать, может быть вещественным или комплексным.
Переменная дифференцирования должна быть простой неиндексированной переменной.
II. Геометрический смысл производной.
ПРИМЕР 2
Дана функция у=f(x). Построить график функции и касательную к графику в точке с абсциссой x=x0, если 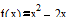

 - уравнение касательной.
- уравнение касательной.
Решение:
Введем данную функцию и найдем ее значение в точке  :
:



Найдем значение производной данной функции в точке  :
:


Запишем уравнение касательной для данной функции:
|
|
|

Построим график данной функции и касательную к ней.


|
|
|


