 |
Задания для самостоятельного выполнения.
|
|
|
|
Задание 1. Найти производную функции в произвольной точке.
1.  5.
5. 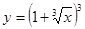 9.
9. 
2.  6.
6.  10.
10. 
3.  7.
7. 
4.  8.
8. 
Задание 2.
Дана функция y=f(x). Построить график функции и касательную к графику в точке с абсциссой x=x0. Y=f(x0)(x-x0)+f(x0) – уравнение касательной.
1. 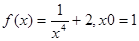 6.
6. 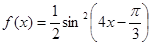 , x0=π∕6
, x0=π∕6
2.  , x0=2 7.
, x0=2 7.  , x0=-1
, x0=-1
3. 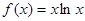 , x0=e 8.
, x0=e 8.  , x0=-π/2
, x0=-π/2
4.  , x0=-1 9.
, x0=-1 9.  , x0=3
, x0=3
5. 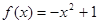 , x0=1 10.
, x0=1 10.  , x0=-2
, x0=-2
ЛАБОРАТОРНАЯ РАБОТА №4.
Тема. Интегральное исчисление.
Цель. Научиться находить определенные интегралы функций, вычислять площадь фигуры при помощи интеграла.
Краткие сведения.
I. Определенный интеграл.
Оператор интегрирования в Mathcad предназначен для численного вычисления определенного интеграла функции по некоторому интервалу.
Знак интеграла выводится при нажатии клавиши со знаком &.
Для того, чтобы вычислить определенный интеграл, необходимо сделать следующее:
Ø Щелкнуть в свободном месте и набрать знак &. Появится знак интеграла с пустыми полями для подынтегрального выражения, пределов интегрирования и переменной интегрирования: ∫
Ø Щелкнуть на поле внизу и набрать нижний предел интегрирования. Щелкнуть на верхнем поле и набрать верхний предел интегрирования.
Ø Щелкнуть на поле между знаком интеграла и d и набрать выражение, которое нужно интегрировать.
Ø Щелкнуть на последнее пустое поле и набрать переменную интегрирования.
Ø Чтобы увидеть результат, нажать знак =.
ПРИМЕР 1 Вычислить определенный интеграл  от 0 до p/4.
от 0 до p/4.
Решение:
|
|
|
Введем знак интеграла и заполним пустые поля;
вычислим интеграл:
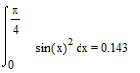
Помните!
Ø Пределы интегрирования должны быть вещественными. Выражение, которое нужно интегрировать может быть вещественным, либо комплексным.
Ø Кроме переменной интегрирования, все переменные в подынтегральном выражении должны быть определены ранее в другом месте рабочего документа.
Ø Переменная интегрирования должна быть простой переменной без индекса.
Ø Если переменная интегрирования является размерной величиной, верхний и нижний пределы интегрирования должны иметь ту же самую размерность.
II. Площадь фигуры.
Как известно, при помощи определенного интеграла можно вычислять площадь фигуры.
ПРИМЕР 2. Найти площадь фигуры, ограниченной графиками функций:

Решение.
Построим графики этих функций в одном графическом блоке:




Вычислим площадь полученной фигуры:
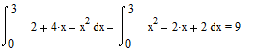 (кв.ед.)
(кв.ед.)
Задания для самостоятельного выполнения.
Задание 1. Вычислить определенный интеграл.
1.  5.
5.  9.
9.  dx
dx
2.  6.
6.  10.
10. 
3.  7.
7. 
4.  8.
8. 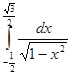
Задание 2. Найти площадь фигуры, ограниченной графиками функций. Построить эту фигуру.
1.  6.
6. 
2. 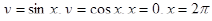 7.
7. 
3. 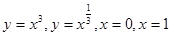 8.
8. 
4. 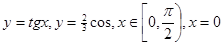 9.
9. 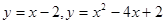
5.  10.
10. 
ЛАБОРАТОРНАЯ РАБОТА №5.
Тема. Построение графиков функций.
Цель. Познакомиться с основными действиями при создании графика в
Mathcad. Научиться строить декартов график, графики поверхности, полярные
графики.
Краткие сведения.
I. Основные действия при создании графика.
Чтобы создать график, необходимо проверить следующие операции:
Ø Предварительно определить аргумент и функцию аргумента, для которой будет строиться график. Аргумент задается диапазонной переменной, а функция аргумента – функцией пользователя.
|
|
|
Например: х:=0,0.1..π
Y(x):=sin(x)
Ø Щелкнуть мышью там, где нужно создать график.
Ø Выбрать Декартов график из меню Графика. При этом на экране появится «заготовка» графика с шестью полями ввода, по три на каждой оси.
Ø Чтобы увидеть график, необходимо заполнить пустые поля:
- Пустое поле в середине горизонтальной оси предназначено для независимой переменной графика. Нужно ввести в это пустое поле дискретную переменную, переменную с индексом или любое выражение, содержащее дискретную переменную.
- Пустое поле в середине вертикальной оси содержит выражение, график которого нужно построить. Нужно ввести в это пустое поле дискретную переменную или любое выражение, содержащее дискретную переменную, находящуюся на горизонтальной оси.
- Другие 4 пустые поля могут использоваться, чтобы отменить автоматический выбор границ на осях координат в Mathcad.
- Нажать <Enter>. В указанном прямоугольнике появляется график функции.
Для того, чтобы вывести функцию на график необходимо сделать следующее:
× Напечатать выражение, график которого нужно получить, в среднее поле на оси ординат и напечатать х в среднем поле на оси абсцисс.
Можно также определить функцию f(x) и поместить ее в среднее пустое поле оси ординат. Это особенно полезно для функций, представляемых громоздким выражением.
ПРИМЕР 1. Построить график функции 
Решение:
Определим аргумент и функцию аргумента, для которой будет строиться график.


Построим график этой функции.

III. Размещение нескольких графиков на чертеже.
Можно построить несколько кривых на одном и том же чертеже – для этого достаточно определить их и перечислить в виде списка в шаблоне графика.
График может содержать несколько выражений по оси ординат в зависимости от одного выражения по оси ординат, согласованных с соответствующими выражениями по оси абсцисс.
Например, чтобы представить графически несколько выражений по оси ординат относительно одного выражения по оси абсцисс, необходимо:
× Вести первое выражение для оси ординат, сопровождаемое запятой. Непосредственно под первым выражением появится пустое поле.
|
|
|
× Ввести в это пустое поле второе выражение, сопровождаемое другой запятой, чтобы получить другое пустое поле и т.д.
Помните! Все выражения должны использовать одну и ту же дискретную переменную.
Можно построить несколько независимых кривых на одном чертеже. Для этого необходимо:
× Ввести два или более выражения, отделяемых запятыми на оси абсцисс, и то же самое число выражений на оси ординат. Mathcad согласует выражения попарно – первое выражение оси абсцисс с первым выражением оси ординат, второе со вторым и т.д. Затем рисуется график каждой пары.
Помните! Каждая согласованная пара выражений должна использовать одну дискретную переменную. Дискретная переменная для одной согласованной пары не должна быть дискретной переменной для других пар.
ПРИМЕР 2 Построить графики трех функций,зависящих от одной переменной х, в пределах одного графического блока:

Решение.
Определим аргумент и функции аргумента, для которых будут строиться графики.




Построим графики данных функций.

IV. Построение графиков поверхностей.
Трехмерные графики в Mathcad отображают графически матрицы значений.
Чтобы создать график поверхности, необходимо:
× Определить матрицу значений, которую необходимо отобразить графически. Mathcad будет использовать номер строки и столбца матрицы в качестве координат по осям X и Y. Элементы матрицы будут представлены на графике как высоты выше или ниже плоскости X-Y.
× Выбрать График поверхности из меню Графика. Mathcad покажет рамку с одним полем ввода.
× Напечатать имя матрицы в этом поле. Затем нажать клавишу [F9] или, в автоматическом режиме, щелкнуть мышью вне выделенной графической области.
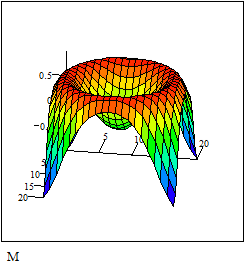
ПРИМЕР 3. Построить график поверхности f(x,y)=sin(x+y)
Определим функцию двух переменных:

Допустим, что по осям x и y необходимо 20 точек. Определим дискретные аргументы i и j, чтобы индексировать эти точки.


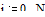
Определим x и y как равномерно располагаемые точки на осях X и Y.


Заполним матрицу М значениями F(x, y)

Выберем График поверхности из меню Графика. Напечатаем М в поле ввода и щелкнем вне графической области.
|
|
|
V. Построение полярного графика.
Для отображения функций, которые неудобно воспроизводить в декартовых координатах, можно строить полярные графики.
Чтобы создать график в полярных координатах, необходимо:
× Выбрать Полярный график из меню Графика. Mathcad показывает круг с четырьмя полями ввода.
× Выше области графика определить угол Q и функцию угла R(Q).
× Поле ввода внизу предназначено для угловой переменной графика. Ввести туда дискретную переменную или любое выражение, включающее дискретную переменную.
× Поле ввода слева должно содержать выражение для радиуса.
× Два поля ввода справа предназначены для верхнего и нижнего граничных значений радиуса. Mathcad заполняет эти поля по умолчанию.
В Mathcad полярные графики рисуются путем замены R и Q на декартовы координаты x и y с использованием стандартных преобразований x=Rcos(Q) и y=Rsin(Q). Предполагается, что R и Q могут принимать и положительные, и отрицательные значения.
ПРИМЕР 4. Построить график функции R(Q)=cos(Q)+1
Определим приращение для Q:

Определим Q как дискретный аргумент с заданным приращением:
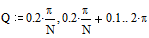
Определим R(Q) как функцию Q:

Отобразим график R(Q) в полярных координатах.

Помните! Mathcad не обрабатывает график, пока вы не нажмете [F9], или, в автоматическом режиме, не щелкните мышью вне области графика.
|
|
|


