Модель канала связи, в котором действуют шумы

ДИСКРЕТНЫЕ КАНАЛЫ С ШУМАМИ

 

Ввиду наличия шумов в канале передачи информации нарушается соответствие между переданными и принятыми сообщениями. Чем выше уровень шумов, тем сильнее нарушается это соответствие. Наиболее интересные и важные результаты теории информации были получены при рас­смотрении передачи информации по каналам связи с шумами. В этом случае безызбыточное кодирование приведет к безвозвратным поте­рям информации: искаженный символ нельзя ни обнаружить, ни испра­вить. Для борьбы с влиянием помех необходимо ввести избыточность в сигнал. Основываясь на интуитивных соображениях (например, на опыте многократного повторения), легко прийти к выводу, что при неограни­ченном повышении требований к малости вероятности ошибки избыточ­ность при любом способе кодирования должна неограниченно возрас­тать, а скорость передачи – стремиться к нулю. Здесь мы имеем яркий при­мер того, как сильно интуиция может привести к заблуждению. Шэннон показал, что существуют такие способы введения избыточности, при которых обеспечиваются одновременно и сколь угодно малая вероят­ность ошибки, и конечная (отличная от нуля) скорость передачи инфор­мации, причем эта скорость может быть сколь угодно близкой к про­пускной способности канала.

Воздей­ствие различного рода помех и собственных шумов (в общем случае будем говорить о шумах) на всякий реальный канал связи приводит к искажению передаваемых сигналов, в результате чего, получив сигнал на приемной стороне, мы не можем с полной достоверностью утверждать, какое сообщение было передано, ибо искажение сигнала шумами может привести к тому, что при передаче сообщения x_i на приемной стороне будет зарегистрировано некоторое другое сообще­ние x_j,где j не совпадает с i.

Пусть, например, множество возможных значений входного сигнала дис­кретного канала, образующие внешний алфавит системы, равно X = { x_i,..., х_т }. Обозначим алфавит адресата (множество возможных значений принимаемого сигнала) через Y = { y ₁, у ₂,..., y_m }.Существует взаимно однозначное и извест­ное адресату отображение j: X ® Y,такое, например, как показано на рис. 8.1 а.

 

 

Рис. 8.1. Передача сигналов по дискретному каналу

При отсутствии помех в канале связи ошибок не происходит, что позволяет по принятому символу y_i точно (безошибочно) вос­становить символ x_i. Действие помех разрушает однозначность ото­бражения j. Переданный символ x_i в принципе при наличии помех может быть принят в виде любого символа алфавита Y (рис. 8.1 б). В то же время если получен символ y_i,то достоверно это означает лишь тот факт, что был передан один из возможных сим­волов алфавита X (рис. 8.1 в).

Если нам известны априорные статистические характеристики источника сообщений, а также характеристики помех, воздействующих на канал, то, получив сообщение, мы можем лишь узнать новое апостериорное распределение вероятности передачи различных сооб­щений), с помощью которого можно вычислить вероят­ность правильного решения о том, какое из возможных сообщений было передано. Таким образом, работа информационного канала с математической точки зрения, в конечном счете, сводится к изме­нению на приемной стороне распределения вероятностей передачи различных сообщений.

Ясно, что на практике мы не можем довольствоваться лишь вы­числением апостериорного распределения, а аппаратура всегда строится таким образом, что в ней с тем или иным риском (вероятностью ошибки) принимается решение о том, какое сообщение было передано.

В схеме рис. 7.1 в случае воздействия помех нет однозначного соответствия между сигналами на входе канала связи (у) и сигналами на его выходе (z). При передаче сигнала y_i выходные сигналы (z) могут принимать различные значения в зависимости от того, каков был шум в момент приема. В общем случае сигнал z может при­нимать непрерывное (бесконечно большое число) множество различ­ных значений.

Для ослабления действия шумов в информационную систему вводят два дополнительных устрой­ства— кодер II и декодер I (рис. 8.2). Назначение второго кодера состоит в реализации помехоустойчивого кодиро­вания сигналов.

 

Рис. 8.2. Блок-схема дискретного канала связи с шумами

 

 

Назначение декодера I состоит в том, чтобы восста­навливать по принятому сигналу соответствующий сигнал на выходе кодера I.

Функции, выполняемые кодером I и декодером II, та­кие же, как в схеме на рис. 7.1.

Рассмотрим передачу дискретных сообщений по каналу с шумом более подробно. Для этого воспользуемся представлением сигналов в линейном пространстве. Ранее была определена математическая модель сигнала в виде абстрактного математического пространства (пространства сигналов).

Естественно, что в пространстве сигнала точек должно быть не меньше, чем возможных сообщений источника информации. При равенстве числа точек и числа возможных сообщений между эле­ментами пространства сигналов и элементами множества возмож­ных сообщений устанавливается одно из возможных взаимно одно­значных соответствий – некоторое отображение множества воз­можных сообщений в пространство сигнала. Это отображение реа­лизуется в передатчике системы связи в форме соответствующего» правила преобразования сообщения в сигнал. Сигналы, представ­ляемые в пространствах, число элементов которых равно числу воз­можных сообщений, обладают низкой устойчивостью к помехам.

Для повышения помехоустойчивости процесса передачи инфор­мации в системах связи используют сигналы с большим числом со­стояний, чем это необходимо для кодирования всех возможных со­общений, и, следовательно, число точек соответствующих про­странств превышает число возможных сообщений. Тогда возникает вопрос: какие точки пространства сигнала сопоставлять возможным сообщениям источника информации?

На данный вопрос нельзя ответить однозначно. Ответ зависит от многих факторов: от статистических свойств потока сообщений, соотношения энергетических характеристик сигнала и помехи, ста­тистических свойств помехи и др. Тем не менее имеются некото­рые общие предпосылки.

Кодер вносит в сигналы избыточность, увеличивая длитель­ность кодовых слов.

Число возможных последовательностей сразу резко увеличивается, но избыточность и состоит в том, что к отправке предназначаются не все из них, а лишь разрешенные. Число всевозможных последовательностей длины п равно 2^nH(X), а число разрешенных к отправке равно 2 ^пН < 2 ^{пН ( X )}(считаем, что энтропия исчисляется в битах); Н –энтропия на символ во множестве разрешенных к отправке после­довательностей («энтропия источника», или «скорость создания инфор­мации»), Н (Х)–энтропия на символ во множестве всевозможных последовательностей. В результате воздействия шумов какие-то из сим­волов отправленной последовательности подменяются другими и на приемный конец поступает другая, отличная от отправленной, после­довательность. Поскольку р (х\у)считается известным, каждой приня­той последовательности соответствует 2 ^{nH ( X|Y )}возможно отправленных.

Декодирование (т.е. принятие решения о том, какая последовательность была отправлена) можно выразить как разбиение всего множества Y принимаемых последовательностей на 2 ^nH подмножеств, сопоставляе­мых с разрешенными к отправке: если, например, принят сигнал i -й группы, то считается, что был послан i -й разрешенный сигнал, который тут же выдается в «чистом» виде получателю.

 

Рассмотрим вопрос о введении избыточно­сти вторым кодирующим устройством на примере равно­мерного кода.

Пусть на выходе кодера I появляются двоичные кодовые слова одинаковой длины μ, соответствующие передаваемым сообщениям. Чтобы декодер I имел возможность обнаруживать и исправлять ошибки, 2-е кодирующее устройство по некоторому правилу добавляет μ _k корректирующих двоичных символов к каждому кодовому слову, поступающему на его вход. В результате получаются кодовые слова длиной μ + μ _k символов, которые затем передаются по линии связи с шумами, где некоторые символы искажаются (символ «1» подменяется символом «0», а символ «0» – символом «1»).

При этом число различных передаваемых кодовых слов меньше числа всех возможных кодовых слов, получаемых на выходе линии связи, т. е.

 

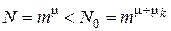, (8.1)

 

где т – число различных кодовых символов,

N различных передаваемых кодовых слов,это разрешенные слова, a N ₀ – N кодовых слов – запрещенные. Если в результате ошибок переданное (разрешенное) кодовое слово перейдет в одно из запрещен­ных, ошибка будет обнаружена декодером I при условии, что в его запоминающем устройстве хранятся все разрешенные кодовые слова. Если же в результате оши­бок переданная комбинация превращается в одну из разрешенных, ошибка декодером I не обнаруживается.

Таким образом, корректирующий код, удовлетворя­ющий условию (8.1), способен в N (N ₀ – N) случаях обна­руживать ошибки из общего числа N ₀ N. Однако если N << N ₀, разрешенные комбинации могут быть выбраны с учетом вероятностных свойств шума так, чтобы вероят­ность получения ошибочной разрешенной комбинации была очень мала. Другими словами, при N << N ₀ в ре­зультате ошибочного приема отдельных символов приня­тое кодовое слово, как правило, окажется запрещенным, что и укажет на ошибку.

Для принятия однозначного решения о том, какое ко­довое слово было отправлено, в общем случае все мно­жество принимаемых кодовых слов N ₀разбивается по некоторому правилу на N подмножеств. Каждое подмноже­ство отождествляется с одним из разрешенных кодовых слов. Если, например, принятое кодовое слово попало в i -е подмножество, считается, что было передано i -е кодовое слово. Задача состоит в том, чтобы выяснить, сущест­вуют ли такие правила введения корректирующих симво­лов в передаваемые кодовые слова и разбиения на под­множества всех возможных принимаемых кодовых слов, при которых вероятность ошибочного приема будет как угодно мала, а скорость передачи как угодно близка к пропускной способности линии связи.

Эта задача в общем виде разрешается теоремами Шеннона о кодировании в присутствии шумов.

 

1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: