 |
Первая теорема Шеннона о кодировании в присутствии шумов.
|
|
|
|
При любой производительности источника сообщений Н, меньшей, чем пропускная способность канала С, существует такой способ кодирования, который позволяет обеспечить передачу всей информации, создаваемой источником сообщений, со сколь угодно малой вероятностью ошибки.
Хотя доказательство этой теоремы, предложенной Шенноном, в дальнейшем подвергалось более глубокому и строгому математическому представлению[19], идея его осталась неизменной. Доказывается только существование искомого способа кодирования, для чего находят среднюю вероятность ошибки по всем возможным способам кодирования и показывают, что она может быть сделана меньше сколь угодно малой величины e. При этом существует хотя бы один способ кодирования, для которого вероятность ошибки меньше средней.
Доказательство теоремы. Пусть H(x) и H(x| y) – априорная и апостериорная энтропии на символ (со стороны приемного конца) для системы, реализующей пропускную способность С канала. В силу свойства Е при достаточно большой длительности (п символов) передачи все возможные любого ансамбля распадаются на высоковероятную и маловероятную группы; при этом о количестве сигналов в соответствующих группах можно сделать следующие утверждения:
а) Группа высоковероятных передаваемых сигналов содержит около 2 пН(х) последовательностей.
б) Группа высоковероятных принимаемых сигналов содержит около 2 пН(у) последовательностей.
в) Каждый высоковероятный принимаемый сигнал мог (с приблизительно одинаковыми вероятностями) произойти от примерно 2 пН(х|у) передаваемых сигналов высоковероятной группы.
г) Каждому отправляемому сигналу из высоковероятной группы может (с приблизительно одинаковыми вероятностями) соответствовать примерно 2 пН(у| х) принимаемых высоковероятных сигналов.
|
|
|
В силу свойства Е энтропии дискретных процессов, при увеличении п все соответствующие e и d будут стремиться к нулю.
Пусть теперь по тому же каналу передается информация со скоростью на входе, равной Н < С. При этом число высоковероятных отправляемых сигналов длиной в п символов будет равно 2 пН < 2 пН(х). Как уже отмечалось, проблема выбора определенного кода состоит в указании того, какие именно из 2 пН(х) возможных последовательностей выбираются в качестве 2 пН разрешенных к отправке, и как разбиваются на 2 пН подгрупп 2 пН(у) выходных последовательностей. Рассмотрим класс всевозможных кодов, которые получатся, если 2 пН разрешенных последовательностей размещать случайным образом среди 2 пН(х) возможных сигналов высоковероятной группы; найдем среднее значение вероятности ошибки для этих кодов.
Пусть принят некоторый сигнал ук. Вероятность ошибки при этом равна вероятности того, что данный сигнал может происходить более чем от одного из 2 пН разрешенных сигналов. Поскольку код получается случайным (равновероятным) выбором 2 пН последовательностей из 2 пН(х), то вероятность того, что заданный сигнал на входе канала попадет в число разрешенных, равна
(8.21)
Принятому сигналу ук соответствует 2 пН(х| у) возможно отправленных сигналов. Отсюда средняя вероятность того, что ни один из 2 пН(х| у) сигналов (кроме одного действительно отправленного) не является разрешенным, равна (пренебрегаем единицей по сравнению с пН(х| у))
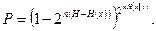(8.22)
Это есть средняя вероятность безошибочного приема. Далее, так как Н < С = Н(х) – Н(х| у), то
Н – Н(х) = - Н(х| у) - h, (8.23)
Где h > 0. Подставляя (8.23) в (8.22), получаем
(8.24)
Можно показать [7], что
(8.25)
т.е. что при случайном кодировании достаточно длинными блоками средняя вероятность ошибки может быть сделана сколь угодно малой. Утверждение о существовании по крайней мере одного кода, дающего вероятность ошибки меньше средней, завершает доказательство.
|
|
|
Отметим, что равенство (8.25) справедливо при любом, сколь угодно малом положительном h. Это означает, что теорема допускает условие Н £ С.
Это и придает особый смысл понятию пропускной способности: пропускная способность оказывается не просто максимально возможной скоростью передачи информации, но максимальной скоростью, при которой еще возможна передача со сколь угодно малой вероятностью ошибки.
Вторая теорема Шеннона о кодировании в присутствии шумов. Для обеспечения достаточной помехоустойчивости приходится вводить в передаваемый сигнал избыточность, уменьшая тем самым скорость передачи информации. Вполне естественно опасение, что при усилении ограничений на малость вероятности ошибки необходимая избыточность будет возрастать, прогрессивно снижая скорость передачи информации, возможно, до нуля. Однако все сомнения снимаются Второй теоремой Шеннона о кодировании для каналов с шумами, которая может быть сформулирована следующим образом:
Теорема. При условии Н £ С среди кодов, обеспечивающих (согласно Первой теореме) сколь угодно малую вероятность ошибки, существует код, при котором скорость передачи информации R сколь угодно близка к скорости создания информации Н.
Скорость передачи информации (на символ) определяется как
R = H – H(x| y), (8.26)
где Н(х| у) – апостериорная энтропия отправленного сигнала на символ, или рассеяние информации в канале.
Доказательство теоремы (см. [7]) начинается с утверждения о том, что минимальная необходимая избыточность на символ равна Н(х| у) добавочных символов. Далее показывают, что код можно выбрать так, чтобы Н(х| у) была сколь угодно малой величиной.
Обсуждение теорем. В первую очередь отметим фундаментальность полученных результатов. Теоремы устанавливает теоретический предел возможной эффективности системы при достоверной передаче информации. Опровергнуто казавшееся интуитивно правильным представление о том, что достижение сколь угодно малой вероятности ошибки в случае передачи информации по каналу с помехами возможно лишь при введении бесконечно большой избыточности, т.е. при уменьшении скорости передачи до нуля. Из теорем следует, что помехи в канале не накладывают ограничений на точность передачи. Ограничение накладывается только на скорость передачи, при которой может быть достигнута сколь угодно высокая достоверность передачи.
|
|
|
Теоремы неконструктивны в том смысле, что в них не затрагивается вопрос о путях построения кодов, обеспечивающих указанную идеальную передачу. Однако, обосновав принципиальную возможность такого кодирования, они мобилизовали усилия ученых на разработку конкретных кодов.
Следует отметить, что при любой конечной скорости передачи информации вплоть до пропускной способности сколь угодно малая вероятность ошибки достигается лишь при безграничном увеличении длительности кодируемых последовательностей знаков. Таким образом, безошибочная передача при наличии помех возможна лишь теоретически.
Обеспечение передачи информации с весьма малой вероятностью ошибки и достаточно высокой эффективностью возможно при кодировании чрезвычайно длинных последовательностей знаков. На практике степень достоверности и эффективности ограничивается двумя факторами: размерами и стоимостью аппаратуры кодирования и декодирования и временем задержки передаваемого сообщения. В настоящее время используются относительно простые методы кодирования, которые не реализуют возможностей, указанных теорией. Однако постоянно растущие требования в отношении достоверности передачи и успехи в технологии создания больших интегральных схем способствуют внедрению для указанных целей все более сложного оборудования.
Следует, однако, иметь в виду, что теоремы для дискретных каналов с шумами, так же как и теорема 2 для каналов без шумов, не утверждает, что кодирование длинных последовательностей сообщений является единственным методом эффективного кодирования. Смысл этих теорем состоит в утверждении существования эффективных методов кодирования и в установлении количественных пределов максимально возможной скорости передачи информации. В связи с этим важными являются не только прямые, но и обратные утверждения этих теорем. Из доказательства теорем вытекает лишь, что кодированием достаточно длинных последовательностей сообщений всегда можно как угодно близко подойти к максимально возможной скорости передачи сообщений (при минимальной вероятности ошибки для каналов с шумами). Последнее, однако, не означает, что не могут существовать другие способы эффективного кодирования. Наоборот, на ряде частных примеров можно показать, что такие способы существуют.
|
|
|
К сожалению, в настоящее время не найдено еще общих способов построения эффективных кодов для каналов с шумами, удовлетворяющих различным требованиям практики. Постепенно, однако, такие способы выявляются. Весьма интересным и важным является утверждение теоремы о том, что в канале с шумами при сколь угодно малой ненадежности передачи сообщений (
→0) скорость передачи информации может быть как угодно близкой к СС. Ранее господствовало мнение, основанное на интуитивных соображениях, что при этих требованиях скорость передачи информации должна неограниченно уменьшаться.
Фундаментальное значение теорем состоит в том, что они позволяют, зная предельные (теоретические) значения скорости передачи информации СС, оценить эффективность используемых методов кодирования.
Итак, приведенные теоремы являются теоремами существования.
Из доказательства этих теорем не следует, каким образом построить код и произвести декодирование, чтобы вероятность ошибки была как угодно мала, а скорость передачи как угодно близка к пропускной способности линии связи. Теоремы носят асимптотический характер, т.е. не являются конструктивными. Однако уже само знание потенциальных возможностей имеет огромное значение: сравнение характеристик реальных систем с теоретическими пределами позволяет судить о достигнутом уровне и о целесообразности дальнейших затрат на его повышение. Прикладные же вопросы рассматриваются в специальном разделе теории информации – теории кодирования, которая изучает способы построения конкретных кодов и их свойства, в частности точные или граничные зависимости вероятностей ошибок от параметров кода.
Обратная теорема Шеннона для каналов с шумами. Обратная теорема указывает условия, которые возникают при передаче информации по каналу с шумами со скоростью, превышающей пропускную способность.
Теорема. Если скорость создания информации Н больше пропускной способности канала С, то никакой код не может сделать вероятность ошибки сколь угодно малой. Минимальное рассеяние информации на символ, достижимое при Н > С, равно Н – С; никакой код не может обеспечить меньшего рассеяния информации.
|
|
|
С доказательством Обратной теоремы Шеннона можно ознакомиться в [4].
Обратная теорема утверждает, что при Н > С безошибочная передача невозможна; при этом чем больше отношение Н / C, тем больше остаточная неопределенность Н(х| у). Последняя связана с вероятностью ошибки при приеме. Естественно возникает вопрос о том, как связана минимальная вероятность ошибки, достигаемая при наилучшем кодировании, с отношением Н/ С. Для бинарного канала решение приведено в [7]. При к = Н/C < 1 вероятность ошибки e(к) = 0 согласно первой теореме. При к ® ¥ e(к) ® 0,5, что означает, что доля передаваемой информации из всей поступающей на вход канала стремится к нулю при к ® ¥; чем быстрее ведется передача, тем меньшее количество информации передается.
Контрольные вопросы
1. Дайте обоснование необходимости введения избыточности при кодировании в канале с помехами.
2. Как определяется среднее количество информации (на один символ), переданной по дискретному каналу с шумами?
3. Как определяется скорость передачи и пропускная способность канала с помехами?
4. Сформулируйте и поясните прямую и обратную теоремы Шеннона о кодировании для канала с помехами.
5. Какие соотношения следуют из теоремы об асимптотической равновероятности достаточно длинных типичных цепочек для стационарных каналов с шумами?
6. Какова причина целесообразности кодирования длинных последовательностей символов?
7. Какой формулой определяется пропускная способность двоичного симметричного канала без памяти, при каком условии пропускная способность этого канала обращается в нуль?
|
|
|
