Пропускная способность дискретного канала связи с шумами

 

Соотношения (7.1)–(7.3), определяющие скорость пе­редачи и пропускную способность канала и линии связи, являются общими, и поэтому они при­менимы как для дискретных, так и для непрерывных ка­налов, как для каналов без шумов, так и для каналов с шумами. Разница заключается в способе вычисления ко­личества информации, содержащейся в последовательности выходных сигналов Z_T, о входных сигналах Y_T, т.е. I (Z_T, Y_T).

Для вычисления I (Z_T, Y_T) можно использовать соотношения (5.30) или (5.31). Из этих соотношений получаем

I(Z_T,Y_T) = H(Z_T) – H(Z_T ‌ | Y_T) = H(Y_T) – H(Y_T | Z_T). (8.9)

 

Будем полагать, что шумы, действующие в канале связи, имеют эргодический характер. Это значит, что, например, при длительной многократной передаче сигнала у_i сигналы z на выходе канала с вероятностью, как угодно близкой к единице, образуют типичную последовательность. То же самое справедливо и при передаче эргодической последовательности различных сигналов у. При таком условии выход канала связи может рассматриваться как эргодический источник.

Для последовательности длительностью Т, содержащей М сигналов такого источника, имеем

H(Z_T) = MH(Z), (8.10)

где H(Z) – энтропия выходного сигнала или, точнее, энтропия выхода канала связи, рассматриваемого как эргодический источник.

Величина H(Z) может быть подсчитана по формуле, аналогичной (6.10),

H(Z) = (8.11)

При этом Q_l и Q_k обозначены характерные состояния выхода канала связи.

Такое же соотношение получим и для вычисления условной энтропии

H(Z_T | Y_T) = MH(Z | Y), (8.12)

где H(Z | Y) – энтропия выходного сигнала канала связи при известных входных сигналах.

Повторяя рассуждения, приведенные при выводе (6.10), получим

H(Z | Y) = (8.13)

где

(8.14)

При этом p(Q_l | Q_k, y_j) – условная вероятность перехода выхода канала связи из состояния Q_k в состояние Q_l при передаче сигнала y_j.

Из (8.9), (8.10) и (8.12) следует, что

I(Z_T, Y_T) = MH(Z) – MH(Z | Y).

При определении скорости передачи информации по (7.3^’) учтем, что ; при этом, как и ранее, - средняя длительность сигнала одного сообщения. Тогда получим

(8.15)

где

и

Повторяя рассуждения, аналогично найдем

(8.16)

В последнем равенстве - поток информации на выходе кодирующего устройства, характеризует потерю информации, обусловленную действием помех.

Из найденных соотношений и (7.3) следует, что пропускная способность канала связи при наличии помех может быть определена из условия

(8.17)

или

(8.18)

Оба определения равноправны и дают одно и то же значение С_с. Использование того или иного определения дикдуется удобством анализа. При отыскании оптимальных статистических характеристик передаваемых сигналов (у) необходимо иметь в виду следующее:

Характерные состояния выхода канала связи (Q_k, Q_l) могут определяться двумя обстоятельствами:

а) наличием фиксированных ограничений, т.е. запретов, накладываемых на допустимую последовательность передачи различных сигналов, и

б) коррелятивными связями между символами, вызываемыми действием шумов.

Каналы, у которых на каждый передаваемый сигнал (символ) шум воздействует независимоот того, какие сигналы передавались ранее, называются каналами без памяти. В этих каналах шумы не вызывают дополнительных коррелятивных связей между сигналами. В настоящее время основные выводы теории информации получены применительно к каналам без памяти.

Проиллюстрируем вычисление пропускной способности канала на следующем примере.

Пусть требуется определить пропускную способность канала связи, по которому передаются двоичные сигналы со скоростью v_x, если вероятность превращения в результате действия помех каждого из этих сигналов в противоположный равна р (вероятность правильного приема, следовательно, 1 – р). Передаваемые сигналы предполагаются независимыми.

 

 

 

Рис. 8.3. Двоичный симметричный канал

 

В этом случае алфавит Х и алфавит Y состоят из двух символов: Х = (х ₁ ,х ₂), Y =(у ₁, у ₂). Диаграмма рис. 8.3 показывает возможные варианты передачи и соответствующие им вероятности. Такой канал называется симметричным.

Средняя условная энтропия

 

 

Но p (x ₁) + p (x ₂)=1.

Поэтому

 

H (Y ô X)= -p log p – (1 – p)log (1 – p).

 

Отсюда видно, что H (Y ô X)не зависит от характеристик источника, т.е. от р (х ₁)и р (х ₂),и определятся только помехами в канале передачи.

Максимальное количество информации на один символ получается, следовательно, при таком распределении вероятностей р (х_i),при котором оказывается максимальным член H (Y). Но H (Y)не может превосходить величины

H_m (Y)= log m =log 2

 

(что достигается при р (х ₁)= р (х ₂)=1/2.Поэтому имеем:

 

max{ I (Y, X) = log 2 + p log p + (1 – p)log (1 – p)

 

и, следовательно, пропускная способность

 

C = v_x max { I (Y, X)} =

 

= v_x [log 2 + p log p + (1– p)log (1 – p)]. (8.19)

 

Отсюда следует, в частности, что при p = 0,т.е. при отсутствии шумов в канале, имеем максимальное значение С

С _max = v_x log 2.

 

При р =1 также имеем детерминированный случай, когда сигналы х ₁переводятся в сигналы х ₂ и наоборот с вероятностью, равной единице. При этом пропускная способность канала также максимальна.

Минимальное значение пропускная способность имеет при p =1/2(C _max = 0).

Если на вход канала подаются сигналы от всех возможных источников дискретных сообщений с одинаковым количеством символов в единицу времени u = 1/ T и числом элементарных символов т, то выражение для С и, соответственно, для пропускной способности канала в расчете на единицу времени выглядит так:

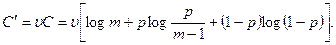(8.20)

 

Отсюда при т = 2 имеем (8.19).

 

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: