Количество информации, передаваемой по каналу связи. Взаимная информация и ее свойства

Количество информации, передаваемое по дискретному каналу связи, может быть определено через информационные характеристики ансамблей сообщений на входе и выходе канала, условные и совмест­ные энтропии этих ансамблей. Свойства энтропии, условной энтропии кладутся в основу при введении важной теоретико-информационной ха­рактеристики канала — взаимной информации между сообщениями на его входе и выходе. Действительно, поскольку при наличии статисти­ческой связи между элементами a и b ансамбля {AB,p(a,b)} значение условной энтропии Н(А | В) в общем случае меньше безусловной и не превосходит ее, т.е. поскольку

(8.2)

можно полагать, что наличие сведений о значении b снижает в сред­нем первоначальную неопределенность относительно ансамбля А. На­зовем величину

(8.3)

количеством информации в сообщении b Î В о сообщении а Î А. (Предполагается, что в ансамбле {АВ,р(а_;b)} не существует элемен­тов с нулевыми вероятностями.)

Поскольку ,

то

(8.4)

т.е. количество информации в сообщении а о сообщении b равно ко­личеству информации в сообщении b о сообщении а. Введенное этим определением количество информации является симметрической функ­цией пары сообщений. Поэтому величину i (а; b) называют количеством взаимной информации между сообщениями а и b или просто взаимной информацией между этими сообщениями.

Формулам (8.3) и (8.4) можно придать симметрическую форму

(8.5)

Определенная таким образом взаимная информация между сооб­щениями a и b является случайной величиной на ансамбле АВ. Введем в рассмотрение ее математическое ожидание (см. § 5.7).

Математическое ожидание случайной величины i(a, b) называется средним количеством взаимной информации или просто взаимной ин­формацией между ансамблями А и В и обознчается через 1{А, В):

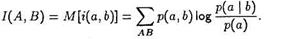(8.6)

Поскольку взаимная информация между сообщениями была опре­делена как разность собственных информации (безусловной и услов­ной), а математическое ожидание собственной информации является по определению энтропией ансамбля, то можно записать:

(8.7)

Основные свойства средней взаимной информации между дискретными ансамблями. Наряду с уже отмеченным свойством симметрии I (A; В) = I(В;А), сформулируем следующие свойства, вытекающие из определения (8.6) и свойств 2 и 3 условной энтропии (см.гл. 5):

— средняя взаимная информация неотрицательна: 1(А; В) ≥ О, причем равенство имеет место тогда и только тогда, когда элементы ансамблей а Î А и b Î В статистически независимы. Доказатель­ство этого утверждения можно провести, используя свойство (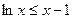) на­турального логарифма.

— средняя взаимная информация между ансамблями A и В не пре­восходит значений энтропии этих ансамблей:

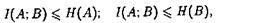(8.8)

причем равенства в (8.8) имеют место, когда каждому фиксирован­ному значению а Î А с вероятностью 1 соответствует определенное значение b Î В и наоборот.

Одно из важнейших свойств средней взаимной информации за­ключается в том, что в процессе преобразований сигналов в различных блоках канала она не может увеличиваться [1]. Это свойство может быть истолковано следующим образом. Пусть В — множество возмож­ных сигналов на выходе некоторого блока канала, а А — множество различных передаваемых сообщений. Доказывается, что никакая обра­ботка наблюдаемых сигналов, при которой производится детерминиро­ванное или случайное их преобразование, не может увеличить средней информации об интересующем нас объекте. Количество информации сохраняется, если преобразование обратимо.