Тема 9. Выборочное наблюдение.

То есть обследованию подвергается только часть единиц совокупности, и данные, полученные на основе отобранной части, являются характерными для всей совокупности.

Основное требование выборочного метода заключается в том, чтобы обеспечить всем единицам совокупности равную возможность быть отобранными для проведения выборочного наблюдения. Выборочное наблюдение дает возможность, не прибегая к сплошному обследованию, получить обобщающие показатели, которые правильно отражают характеристики всей совокупности единиц.

Вся совокупность единиц, из которой производится отбор, принято называть генеральной совокупностью. Численность генеральной совокупности обозначается «N».

Совокупность отобранных единиц из генеральной совокупности для проведения выборочного наблюдения называется выборочной совокупностью. Численность выборочной совокупности обозначается «n».

При выборочном наблюдении дело имеют с двумя категориями обобщающих показателей: относительными и средними величинами.

Если необходимо дать характеристику совокупности по атрибутивному признаку, то используют относительные величины, определяют долю тех единиц (их удельный вес), которые обладают интересующим признаком.

Различают:

– генеральную долю P = ,

где N – число всех случаев;

M – число случаев, благоприятствующих данному событию;

– выборочную долюW = ,

где m – число единиц в выборочной совокупности, обладающих изучаемым признаком;

n – число единиц выборочной совокупности.

Задача выборочного метода наблюдения состоит в том, чтобы на основе выборочной доли дать правильное представление о доле в генеральной совокупности.

Если необходимо дать характеристику совокупности по количественному признаку, то используют средние величины, показатели, характеризующие среднее значение варьирующего признака.

Среднее значение варьирующего признака во всей совокупности (в генеральной совокупности) называется генеральной средней ().

Среднее значение из единиц, которые подверглись выборочному наблюдению, называется выборочной средней ().

В этом случае задача выборочного наблюдения состоит в том, чтобы на основе выборочной средней дать правильное представление о средней в генеральной совокупности.

Так как обследованию подвергается не вся совокупность единиц, а только их часть, то заранее можно сказать, что показатели выборочной совокупности никогда не будут совпадать с показателями, характеризующими всю совокупность. То есть генеральная доля или генеральная средняя всегда будут отличаться от выборочной доли или выборочной средней на какую-то величину. В данном случае нельзя говорить о том, чтобы добиться абсолютного совпадения этих показателей, речь идет о том, чтобы узнать возможные пределы отклонений показателей выборочной совокупности от показателей генеральной совокупности и условия, от которых зависит величина этих отклонений.

Возможные пределы отклонений выборочной доли и выборочной средней от доли и средней в генеральной совокупности носят название ошибки выборочного наблюдения. Ошибки бывают двух видов: тенденциозные, случайные.

Тенденциозные ошибки – когда преднамеренно отбирают лучшие или худшие единицы совокупности.

Случайные ошибки – когда производят случайный отбор единиц совокупности.

Величина средней ошибки выборочного наблюдения может быть рассчитана:

– для количественно изменяющегося признака (ошибки для средней величины):

μ = ;

– для качественно изменяющегося признака:

μ = – средняя ошибка для генеральной доли

и μ = – средняя ошибка для выборочной доли.

Выборочное наблюдение может быть повторным и бесповторным. При бесповторном способе отбора для уточнения ошибки выборки в формулу ошибки вводится дополнительный множитель , где – доля единиц выборочной совокупности в генеральной совокупности. При бесповторном способе отбора средняя ошибки будет иметь вид:

μ =

средняя ошибки для средней величины при бесповторном способе отбора;

μ =

средняя ошибки для генеральной доли при бесповторном способе отбора;

μ =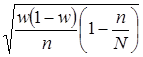

средняя ошибки для выборочной доли при бесповторном способе отбора.

В практике бывает необходимо определить не только величину ошибки, но и пределы, за которые она не должна выходить.

Пределы, за которые не выйдет величина конкретной ошибки выборочного наблюдения, можно установить не с абсолютной достоверностью, а лишь с определенной степенью вероятности.

Доказано, что генеральные характеристики не отклоняются от выборочных

= μ

p = w μ

на величину большую, чем величина ошибки выборочного наблюдения (μ), и всегда имеют равную вероятность 0,683. Т.е. можно утверждать, что из 1000 случаев в 683 случаях выборочная средняя или выборочная доля будут отличаться от генеральной средней или генеральной доли на величину средней ошибки выборочного наблюдения (μ), а в 317 случаях может отличаться больше, чем на 1μ.

Может быть:

= 2μ

p = w 2μ

В этом случае степень вероятности повышается до 0,954.

При = 3μ

p = w 3μ

степень вероятности повышается до 0,997.

Ошибка выборочного наблюдения, исчисленная с заданной степенью вероятности, называется предельной ошибкой выборки ():

Δ= ,

где t – коэффициент доверия (кратности).

Следовательно, величина предельной ошибки выборочного наблюдения зависит от величины средней ошибки и коэффициента доверия, а коэффициент доверия в свою очередь зависит от степени вероятности, с которой проводится выборочное наблюдение.

В зависимости от принятой вероятности определяется значение коэффициента доверия (или кратности) (t) по удвоенной нормированной функции Лапласа:

Ф(t) = ,

где Ф(t) – интеграл Лапласа (см. Приложение 2).

Формулы предельной ошибки выборочного наблюдения можно записать так:

· для количественно изменяющегося признака при бесповторном способе отбора

Δ_х = t ;

· для качественно изменяющегося признака при бесповторном способе отбора

Δ_w = t .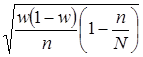

Определение пределов генеральных характеристик с заданной степенью вероятности на основе показателей, полученных по данным выборки, можно выразить следующим образом:

· доверительные интервалы для средней

= Δ_х

– Δ_х + Δ_х ;

· доверительные интервалы для генеральной доли

p = w Δ_w

w – Δ_w p w + Δ_w.

Пример 1. Для определения качества партии товара 3% от всего количества изделий были подвергнуты выборочному обследованию. Из 800 проверенных изделий 200 были нестандартными. Определить с вероятностью 0,954 долю нестандартных изделий во всей партии.

Решение: По условию задачи дано:

= 3% или 0,03

n = 800 изд. Определим долю нестандартных изделий в

m = 200 изд. выборочной совокупности:

t = 2 w = = = 0,25 или 25%.

Из 800 проверенных изделий 25% – нестандартные

w –? Δ_w –? изделия.

Определим предельную ошибку выборочного наблюдения:

Δ_w = t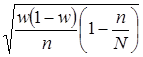

или Δ_w = 2 = 0,03 или 3,0%.

Доверительные интервалы для доли будут равны:

p = w Δ_w

p = 25% 3%, тогда 25% – 3% p 25% + 3%.

Доля нестандартных изделий во всей партии будет находиться в пределах от 22 до 28% при вероятности 0,954.

Пример 2. Для определения среднего срока пользования краткосрочным кредитом в банке была произведена 10%-ная механическая выборка, в которую попало 200 счетов. В результате обследования установлено, что средний срок пользования краткосрочным кредитом – 30 дней при среднем квадратическом отклонении 9 дней. С вероятностью 0,997 определить пределы, в которых будет находиться средний срок пользования краткосрочным кредитом в генеральной совокупности.

Решение. Средний срок пользования кредитом в банке находится в пределах:

– Δ_х + Δ_х .

Так как выборка механическая, то ошибка выборочного наблюдения определяется по формуле:

Δ_х = t ;

Δ_х = 3 = 1,81 2 дня

=30 дн. 2 дн. или 30 дн.–2 дн. 30 дн.+2 дн.

С вероятностью 0,997 можно утверждать, что средний срок пользования краткосрочным кредитом в банке находится в пределах от 28 дней до 32 дней.