 |
Тема 10. Статистические приемы изучения взаимосвязей.
|
|
|
|
Все явления общественной жизни сложны и многообразны, они формируются под действием многочисленных и взаимосвязанных факторов.
В определенных связях и отношениях находятся и статистические показатели. Причем одни показатели статистики выступают как признаки причины, другие – как признаки следствия. Задача анализа заключается в том, чтобы выявить эти связи, а если можно, то измерить тесноту зависимости признака следствия от признака фактора.
Студенту следует усвоить, какие же используются виды взаимосвязей и статистические приемы исследования.
Связи, существующие между статистическими показателями многообразны и различны по характеру. Чтобы их выявить и измерить, применяются различные статистические приемы исследования:
1. Метод группировок – с помощью которого изучают факторные связи. При этом единицы совокупности разбивают на группы по значению признака фактора. В каждой группе исчисляется среднее значение признака фактора и результативного признака. Следствие – между факторным и результативным признаками существует зависимость.
Например, в годовых отчетах сахарных заводов содержатся данные о размерах производственных фондов и среднесуточной переработке сахарной свеклы. Сравнение этих данных обнаруживает, что между размером основных производственных фондов и среднесуточной переработкой сахарной свеклы у отдельных заводов имеют место различные соотношения. В одних случаях среднесуточная переработка сырья возрастает с увеличением производственных фондов, в других случаях имеет место обратное соотношение. В ряде случаев заводы имеют почти одинаковые по размерам производственные фонды, но перерабатывают далеко не одинаковое количество сахарной свеклы в сутки.
|
|
|
Чтобы охарактеризовать зависимость среднесуточной переработки сахарной свеклы от размера стоимости основных производственных фондов, наличие которой теоретически бесспорно, произведем группировку 245 заводов по величине основных производственных фондов (табл. 10.1.).
Таблица 10.1.
Зависимость среднесуточной переработки сахарной свеклы
от размера основных производственных фондов
| Группы заводов по размеру осн. произв. фондов, млн. руб. | Число заводов | Переработано сахарной свеклы, тыс. т | Длительность работы заводов по переработке сах. свеклы, тыс. т | Среднесуточная переработка сах. свеклы, тыс. т |
| А | ||||
| До 2 2 – 4 4 – 6 6 – 8 8 – 10 св. 10 | 8,5 10,9 15,5 15,7 16,6 17,7 | |||
| Итого | 12,5 |
Из таблицы видно, что зависимость между среднесуточной переработкой сахарной свеклы и размером основных производственных фондов есть, и она прямая. Чем больше размер основных производственных фондов, тем больше среднесуточная переработка сахарной свеклы.
2. Индексный метод – при помощи которого изучается компонентный вид связей, когда сложное явление изменяется под влиянием входящих в него компонентов. Например, товарооборот изменяется под влиянием входящих в него компонентов – изменения цен и изменения количества проданных товаров. Для выявления этой зависимости используют систему взаимосвязанных индексов:
I pq = 
,
1,26 =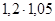 
,
то есть можно сказать, что товарооборот вырос на 26% за счет увеличения цен на 20% и увеличения объема продаж на 5%.
3. Балансовый метод – при помощи которого изучаются связи и пропорции между образованием ресурсов и их распределением. Балансовый метод используется для выявления взаимосвязи между отраслями народного хозяйства, между производством и реализацией продукции, для характеристики региональных связей и т.д. Балансовый метод позволяет также провести увязку и контроль взаимосвязанных статистических показателей.
|
|
|
Это наглядно можно видеть из следующих данных:
Таблица 10.2.
Межрегиональный грузообмен, тыс. т
| Районы отправления | Районы прибытия | Итого отправлено | В том числе вывезено | ||||
| А | Б | В | Г | Д | |||
| А | |||||||
| А Б В Г Д | |||||||
| Итого прибыло, в том числе ввезено | – | – |
Эта таблица показывает межрегиональные связи по грузообороту, а также размер внутрирегионального обмена грузами, выделенный по диагонали таблицы. Так цифра 100, значащаяся против района А как по горизонтали, так и по вертикали, выражает объем грузооборота внутри этого района. Цифра 20 по строке А означает, что из региона А отправлено в район Б 20 тыс. т груза. Вместе с тем таблица показывает, что из района Б отправлено в район А 40 тыс. т груза и т.д.
Таблица дает возможность определить и общий грузообмен каждого региона со всеми остальными регионами. Если из итогов по каждой строке и каждой графе вычесть внутрирайонный грузооборот, то в итогах по строкам будет объем вывоза груза из данного региона в другие регионы, а в итогах по графам – объем ввоза в них.
Например, регион А вывозит в другие регионы всего 85 тыс. тонн грузов, а ввозит180 тыс. т, то есть больше получает грузов, чем отправляет.
4. Корреляционный анализ взаимосвязей. Связи между явлениями могут быть полными (функциональными) и неполными (корреляционными). Для функциональной зависимости характерным является то, что изменение признака следствия целиком определяется изменением признака фактора. Например, площадь круга выражается формулой S = πR2, то есть площадь круга изменяется от изменения квадрата ее радиуса.
Корреляционные связи характеризуются тем, что величина признака следствия изменяется под влиянием нескольких факторов. При этом одни факторы оказывают влияние на все единицы изучаемой совокупности, а другие – только на отдельные из них. Корреляционные связи проявляются отчетливо только в большом числе факторов, так как при этом сглаживаются индивидуальные особенности и второстепенные факторы.
|
|
|
Например, анализируя производительность труда на предприятии, можно видеть зависимость ее от уровня энерговооруженности труда. Но производительность труда зависит и от других факторов: от режима работы предприятия, организации снабжения, квалификации работников и т.д. Поэтому зависимость производительности труда от уровня энерговооруженности труда не может быть полной, а является корреляционной.
При корреляционном анализе связей между явлениями ставятся задачи:
√ Обнаружить в фактическом материале зависимость между изучаемыми показателями.
√ Установить форму связи.
√ Изменить полноту связи между изучаемыми показателями.
Для выявления корреляционных зависимостей используют метод группировок. В этом случае сравниваются не отдельные данные, а групповые средние.
Например, если мы сгруппировали банки по размеру процентной ставки и по каждой группе подсчитали сумму выданных кредитов, то увидели, что между ними существует зависимость, причем обратная, то есть с увеличением размера процентной ставки уменьшается размер суммы выданного банком кредита.
Одним из показателей корреляционной зависимости является эмпирическое корреляционное отношение (η) и коэффициент детерминации (η2):
η = 
,
где 
= 
межгрупповая дисперсия;
= 
– 
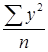общая дисперсия.
η2 = 
коэффициент детерминации говорит о том, какая доля вариации признака обусловлена признаком, положенным в основу группировки.
Эмпирическое корреляционное отношение характеризует тесноту связи между групповым и результативным признаком и изменяется от 0 до +1. Чем ближе эмпирическое корреляционное отношение к 1, тем более тесная связь между изучаемыми признаками.
Пример 1. Для изучения тесноты связи между суммой выданного банком кредита (результативный признак – у) и размером процентной ставки (факторный признак – х) по данным примера 1 в теме 3 вычислить коэффициент детерминации и эмпирическое корреляционное отношение.
|
|
|
Решение: Коэффициент детерминации определяем по формуле (см. выше).
Для расчета межгрупповой дисперсии строим расчетную таблицу.
Таблица 10.3.
|
|
|
