 |
Расчет межгрупповой дисперсии
|
|
|
|
| Группы банков по размеру процентной ставки | Число банков | Сумма выданных кредитов на 1 банк |
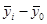
|
(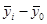 )2 )2
|
(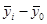 )2n )2n
|
| А | |||||
| 11 – 14 14 – 17 17 – 20 20 – 23 23 – 26 | 26,39 19,62 13,21 6,61 2,25 | 11,26 4,49 -1,92 -8,52 -12,88 | 126,79 20,16 3,69 72,59 165,89 | 507,15 120,96 14,75 217,77 497,68 | |
| Итого | 15,13 | – | – | 1358,31 |
Рассчитаем межгрупповую дисперсию по формуле
 =
=  =67,92.
=67,92.
Для расчета общей дисперсии возведем все значения «у» в квадрат.
Таблица 10.4.
| у | у2 | у | у2 | у | у2 | у | у2 | у | у2 |
| 9,54 13,56 22,33 27,43 | 91,01 183,87 498,63 752,40 | 13,58 3,25 27,7 21,2 | 184,42 10,56 767,29 449,44 | 13,5 2,5 19,63 5,1 | 182,25 6,25 385,34 26,01 | 17,9 12,2 1,0 26,55 | 320,41 148,84 1,00 704,90 | 23,88 20,18 5,2 16,45 | 570,25 407,23 27,04 270,60 |
| 5987,74 |
Рассчитаем общую дисперсию по формуле.
 =
=  – 228,92 = 70,47.
– 228,92 = 70,47.
Тогда коэффициент детерминации будет:
η2 =  = 0,964.
= 0,964.
Он означает, что вариация суммы выданных банком кредитов на 96,4% объясняется вариацией размера процентной ставки и на 3,6% – прочими факторами.
Эмпирическое корреляционное отношение будет равно:
η =  =
=  = 0,98.
= 0,98.
Оно показывает, что связь между суммой выданных банком кредитов и размером процентной ставки очень тесная.
Теоретическую формулу связи выбирают в виде математического уравнения. Например,
уравнения линейной связи: ух = а0 + а1х;
уравнения гиперболы: ух = а0 + а1  ;
;
уравнения параболы 2-го порядка и т.д. ух = а0 + а1х + а2х2.
Если результативный признак с увеличением факторного признака равномерно возрастает или убывает, то такая зависимость является линейной и выражается уравнением прямой:
ух = а0 + а1х,
где у – индивидуальные значения результативного признака;
х – индивидуальные значения факторного признака;
|
|
|
а0, а1 – параметры уравнения прямой (уравнения регрессии);
ух – теоретическое значение результативного признака.
Найти теоретическое уравнение связи – это значит рассчитать параметры прямой линии способом наименьших квадратов, который дает систему двух нормальных уравнений:
 ,
,
где n – число показателей.
Теоретическое уравнение ух = а0 + а1х выражает функциональную зависимость у от х. Это возможно допустить, если прочие факторы, влияющие на у, не оказывают в данном случае существенного влияния. Это бывает, когда корреляционная зависимость между у и х высокая. В этом случае параметр а1 при х в уравнении регрессии приобретает большое практическое значение. Этот параметр, который называется коэффициентом регрессии, характеризует, в какой мере увеличивается ух с ростом величины х.
Пример 2. Имеются выборочные данные по 5 однородным предприятиям:
| Данные | Номер предприятия | ||||
| Энерговооруженность труда 1 рабочего, квт.-ч. | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 |
| Выпуск готовой продукции на 1 рабочего, шт. |
Вычислить уравнение корреляционной связи и построить график.
Решение: Предположим, что между энерговооруженностью труда и выпуском готовой продукции существует линейная корреляционная связь, которую можно выразить уравнением прямой:
ух = а0 + а1х.
Факторным признаком является энерговооруженность труда, а результативным – выпуск готовой продукции.
Вычислим параметры прямой с помощью системы двух нормальных уравнений:
 .
.
Для решения системы построим расчетную таблицу.
Таблица 10.5.
Расчет сумм для вычисления параметров уравнения прямой по несгруппированным данным
| № предприятия | Энерговооружен-ность труда на 1 рабочего, квт.-ч. х | Выпуск продукции на 1 рабочего, шт. у | ху | х2 | ух |
| 1,0 1,5 2,0 2,5 3,0 | 1,0 2,25 4,0 6,25 9,0 | 21,6 24,0 26,4 28,8 31,2 | |||
| Итого | 10,0 | 22,5 |
|
|
|
Подставив в систему нормальных уравнений фактические данные из таблицы 10.5, получим:
+ 
 |
Решим систему методом исключения, то есть умножим каждый член первого уравнения на (-2), получим:
+  .
.
2,5 а1 = 12
Уравнения сложим. Получили 2,5 а1 = 12, откуда
а1 =  = 4,8.
= 4,8.
Подставим значение а1 в первое уравнение и определим а0.:
5 а0+ 48 а1 = 132 а0 =  = 16,8.
= 16,8.
Уравнение регрессии будет иметь вид:
ух = 16,8 + 4,8х.
В нашем уравнении регрессии а1 = 4,8 показывает, что с увеличением энерговооруженности труда одного рабочего на 1 квт.-ч. выпуск готовой продукции возрастает на 4,8 штуки. Построим график корреляционной зависимости между энерговооруженностью труда одного рабочего и выпуском готовой продукции на одного рабочего. Определим все значения ух, подставляя в уравнение все значения х, и данные занесем в таблицу 10.5.
у
|
|
|

Рис. 10.1. График корреляционной зависимости энерговооруженности труда одного рабочего и выпуском готовой продукции на одного рабочего.
Одним из важнейших этапов исследования корреляционной связи является измерение ее тесноты. Для этого применяются: линейный коэффициент корреляции и индекс корреляции.
Индекс корреляции применяется для измерения тесноты связи между признаками при любой форме связи, как линейной, так и нелинейной. Индекс корреляции можно вычислить только после того, как определена форма связи и исчислена теоретическая линия регрессии.
Индекс корреляции рассчитывается по формуле:
R =  ,
,
где  =
=  – общая дисперсия, показывающая вариацию результативного признака под влиянием всех факторов, вызывающих эту вариацию;
– общая дисперсия, показывающая вариацию результативного признака под влиянием всех факторов, вызывающих эту вариацию;
 =
=  – остаточная дисперсия, характеризующая вариацию результативного признака под влиянием прочих неучтенных факторов.
– остаточная дисперсия, характеризующая вариацию результативного признака под влиянием прочих неучтенных факторов.
Индекс корреляции изменяется от 0 до 1: чем ближе индекс к 1, тем теснее связь между признаками.
Частным случаем индекса корреляции является линейный коэффициент корреляции, который применяется только при линейной форме связи:
r =  .
.
В отличие от индекса корреляции линейный коэффициент корреляции показывает не только тесноту связи, но и направление связи (прямая или обратная) и изменяется от –1до +1.
|
|
|
Пример 3. По данным примера 2 измерить тесноту связи между производительностью труда и энерговооруженностью труда линейным коэффициентом корреляции и индексом корреляции.
Решение: Для расчета линейного коэффициента корреляции построим расчетную таблицу.
Таблица 10.6.
Расчет показателей
для определения линейного коэффициента корреляции
| № предприятия | Энерговооружен-ность труда на 1 рабочего, квт.-ч. х | Выпуск готовой продукции на 1 рабочего, шт. у | ху | х2 | у2 |
| 1,0 1,5 2,0 2,5 3,0 | 1,0 2,25 4,0 6,25 9,0 | ||||
| Итого | 10,0 | 22,5 |
Подставим данные таблицы в формулу линейного коэффициента корреляции:
r = 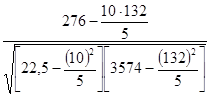 =0,804.
=0,804.
Связь между энерговооруженностью труда и производительностью труда довольно-таки тесная.
Для расчета индекса корреляции необходимо предварительно вычислить общую и остаточную дисперсии, для чего построим расчетную таблицу.
Таблица 10.7.
|
|
|


