 |
Один из видов классических задач линейного программирования связан с проблемой подбора оптимального набора пищевых продуктов для составления диеты.
|
|
|
|
Для того чтобы жить, человек должен ежедневно получать в необходимых количествах белки, жиры, углеводы, витамины, микроэлементы и прочие питательные вещества. Эти вещества попадают в организм с разнообразными пищевыми продуктами.
Задача данной исследовательской работы состоит в определении такого набора продуктов, который, с одной стороны, обеспечивал бы жизненные потребности человека, а с другой – имел бы минимальную стоимость.
III. Задача о диете
Общая формулировка задачи о диете
I. Содержательное описание
Имеется несколько видов продуктов. Определить рацион питания (количество каждого вида продукта) так, чтобы были обеспечены нижние границы норм потребления некоторых питательных веществ, а стоимость рациона была наименьшая. Цены за единицу каждого продукта известны.
II. Математическая модель
2.1. Исходные параметры
 – количество видов продукта
– количество видов продукта
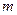 – количество контролируемых питательных веществ
– количество контролируемых питательных веществ
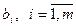 – нормы потребления каждого питательного вещества (нижние границы)
– нормы потребления каждого питательного вещества (нижние границы)
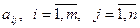 – содержание i-го питательного вещества в единице j-го продукта
– содержание i-го питательного вещества в единице j-го продукта
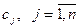 – цена каждого продукта
– цена каждого продукта
2.2. Управляемые параметры (варьируемые параметры)
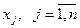 – объем закупок каждого продукта
– объем закупок каждого продукта
 – вектор управляемых параметров (решение, план закупок или рацион)
– вектор управляемых параметров (решение, план закупок или рацион)
2.3. Ограничения модели
Потребление каждого питательного вещества не должно быть ниже нормы.
Пусть 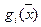 – содержание i-го питательного вещества в произвольном рационе
– содержание i-го питательного вещества в произвольном рационе 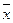 .
.

Нужно выбрать наилучшее решение.
III. Формулировка цели принятия решений
Сформулируем критерий оптимальности. Пусть 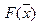 – стоимость произвольного рациона
– стоимость произвольного рациона 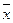 . Требуется найти рацион наименьшей стоимости
. Требуется найти рацион наименьшей стоимости
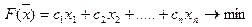
Таким образом, задача о диете ставится как задача определения такого набора управляемых параметров
|
|
|
 ,
,
при которых достигается наименьшее значение критерия
|
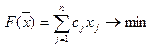
при условии
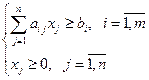
Пример решения общей задачи о диете графическим методом.
Для сохранения здоровья и работоспособности человек должен в сутки потреблять не менее 69 условных ед. белков, не менее 84 условных ед. жиров, не менее 39 условных ед. углеводов. Имеется два вида продуктов 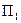 и
и 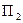 : стоимость единицы каждого из них равна соответственно 4 и 12 ден. ед. Имеем таблицу содержания белков, жиров и углеводов в продуктах П₁ и П₂:
: стоимость единицы каждого из них равна соответственно 4 и 12 ден. ед. Имеем таблицу содержания белков, жиров и углеводов в продуктах П₁ и П₂:
| Белки | Жиры | Углеводы | |
| Продукт П₁ | |||
| Продукт П₂ |
Требуется составить математическую модель задачи, позволяющую сформировать из продуктов П₁ и П₂ суточную диету, которая содержала бы белков, жиров и углеводов не меньше минимальных обоснованных норм и требовала бы минимальных денежных затрат. Решим данную задачу графическим способом.
Решение.
Обозначим через х₁ и х₂ количества единиц соответственно продуктов П₁ и П₂, которые составят суточную диету, а через 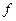 - затраты, связанные с приобретением продуктов. Тогда целевую функцию
- затраты, связанные с приобретением продуктов. Тогда целевую функцию 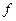 в принятых обозначениях и с учетом цен на продукты можно записать в виде:
в принятых обозначениях и с учетом цен на продукты можно записать в виде:
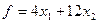 (1.1)
(1.1)
где 4 х₁ - стоимость х₁ единиц продукта П₁, 12 х₂ - стоимость х₂ единиц продукта П₂. Состав (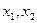 ) суточной диеты должен удовлетворять упомянутым в задаче ограничениям на содержание в нем белков, жиров и углеводов. Например, белков в х₁ единицах продукта П₁ будет присутствовать 3 х₁ усл. ед, белков в х₂ единицах продукта П₂ будет присутствовать 16х₂ условных ед., так что общее количество белка в диете составит 3 х₁ +16х₂ условных единиц. По условию задачи эта сумма должна быть не меньше 69, что можно выразить неравенством:
) суточной диеты должен удовлетворять упомянутым в задаче ограничениям на содержание в нем белков, жиров и углеводов. Например, белков в х₁ единицах продукта П₁ будет присутствовать 3 х₁ усл. ед, белков в х₂ единицах продукта П₂ будет присутствовать 16х₂ условных ед., так что общее количество белка в диете составит 3 х₁ +16х₂ условных единиц. По условию задачи эта сумма должна быть не меньше 69, что можно выразить неравенством:
 (1.2)
(1.2)
|
|
|
Проводя аналогичные рассуждения в отношении жиров и углеводов, получим еще два неравенства, которым должны удовлетворять переменные х₁ и х₂:
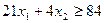 (1.3)
(1.3)
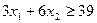 (1.4)
(1.4)
По смыслу задачи переменные 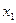 и
и 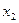 не могут выражаться отрицательными числами, откуда
не могут выражаться отрицательными числами, откуда
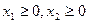 (1.5)
(1.5)
Соотношения (1.1) - (1.5) образуют математическую модель данной задачи. Таким образом, математическая задача состоит в нахождении решения х₁ и х₂ системы неравенств (1.2)-(1.5), доставляющего минимум функции (1.1).
Построим на координатной плоскости (х₁0х₂) область допустимых решений системы неравенств (1.2)-(1.5). Запишем уравнения граничных прямых, соответствующих неравенствам (1.2)-(1.5):
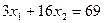 (1.6)
(1.6)
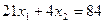 (1.7)
(1.7)
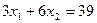 (1.8)
(1.8)
Учитывая, что неравенства (1.5) определяют первую четверть координатной плоскости 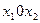 , находим область допустимых решений системы неравенств (1.2)-(1.5), как общую часть (пересечение) всех установленных полуплоскостей. В нашем случае это выпуклая неограниченная многоугольная область с вершинами A, B, C и D (см. рис.).
, находим область допустимых решений системы неравенств (1.2)-(1.5), как общую часть (пересечение) всех установленных полуплоскостей. В нашем случае это выпуклая неограниченная многоугольная область с вершинами A, B, C и D (см. рис.).
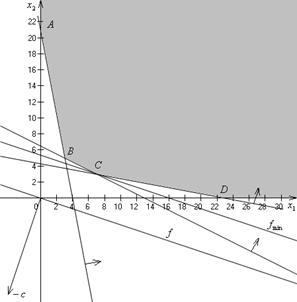
Остается в этой области найти точку, координаты которой доставляют минимум функции (1.1). Из рисунка видно, что последней (крайней) точкой области допустимых решений является точка C. Именно в этой точке функция и достигает наименьшего значения. Координаты точки C находятся в результате совместного решения уравнений прямых (1.6) и (1.8) – граничных прямых BС и СD, пересекающихся в этой точке:3∙х₁+16∙х₂=69; 3∙х₁+6∙х₂=39. Итак, х₁=7; х₂=3 и f=4∙7+12∙3=6. Итак по оптимальному плану в суточную диету следует включить 7 единиц продукта П₁ и 3 единицы продукта П₂. При этом затраты будут минимальными и составят 64 денежных единицы.
|
|
|


