 |
III. Определение параметров объединенной системы.
|
|
|
|
СМО с ограниченным временем пребывания в неограниченной очереди.
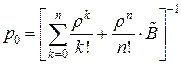 , (44)
, (44)
где
 (45)
(45)
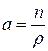 (46)
(46)
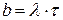 (47)
(47)
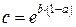 (48)
(48)
 (49)
(49)
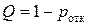 (50)
(50)
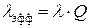 (51)
(51)
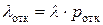 (52)
(52)
 (53)
(53)
где
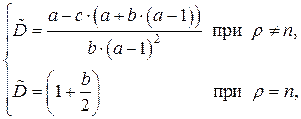 (54)
(54)
Практическая часть
Системы массового обслуживания (СМО).
Во всех задачах на системы массового обслуживания будем считать, что выполнены условия пуассоновского распределения вероятностей ожидания и обслуживания и марковского потока входящих требований.
Задача 1.
Станция автосервиса работает 12 часов в сутки. На станции два здания для рабочих разной специализации. В первом – 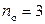 боксов для обслуживания отечественных автомобилей, во втором –
боксов для обслуживания отечественных автомобилей, во втором – 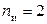 боксов для ремонта «иномарок». Бригада «отечественного» бокса обслуживает отечественный автомобиль в среднем за
боксов для ремонта «иномарок». Бригада «отечественного» бокса обслуживает отечественный автомобиль в среднем за 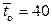 минут, а «иностранная» бригада тратит на иномарку в среднем
минут, а «иностранная» бригада тратит на иномарку в среднем 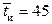 минут. В течение рабочего дня автомобили прибывают на станцию в случайные моменты времени. За день прибывает в среднем
минут. В течение рабочего дня автомобили прибывают на станцию в случайные моменты времени. За день прибывает в среднем  отечественных автомобилей и
отечественных автомобилей и  иномарок. Если хотя бы один из необходимых боксов свободен, то автомобиль сразу же начинает обслуживаться. Если все заняты, то автомобиль занимает свободное место на стоянке около соответствующего здания. Если заняты все места, то он уезжает не обслуженным. Около «отечественного» здания
иномарок. Если хотя бы один из необходимых боксов свободен, то автомобиль сразу же начинает обслуживаться. Если все заняты, то автомобиль занимает свободное место на стоянке около соответствующего здания. Если заняты все места, то он уезжает не обслуженным. Около «отечественного» здания 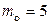 мест, около «иностранного» –
мест, около «иностранного» –  . Средняя прибыль, получаемая с отечественных и иностранных автомобилей, одинакова и равна
. Средняя прибыль, получаемая с отечественных и иностранных автомобилей, одинакова и равна 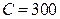 руб. за машину.
руб. за машину.
Компания рассматривает проект объединенной работы двух зданий, при которой каждый поступающий автомобиль без учета специфики поступает в любой свободный бокс или на объединенную стоянку. Известно, «отечественная» бригада будет тратить на иномарки в среднем  минут, а бригада, квалифицирующаяся на иномарках, –
минут, а бригада, квалифицирующаяся на иномарках, –  минут на отечественный автомобиль.
минут на отечественный автомобиль.
|
|
|
® Определить входные параметры этих СМО.
® Определить целесообразность объединения зданий с точки зрения:
o Максимизации средней прибыли компании, при условии, что средняя прибыль, получаемая с отечественных и иностранных автомобилей, одинакова и равна 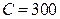 руб. за машину.
руб. за машину.
o Минимизации среднего времени нахождения автомобиля на станции.
Решение задачи 1.
(лучше решать задачу по очереди, для каждой СМО отдельно).
Данная система массового обслуживания – СМО с ограниченной очередью.
I. Найдем входные данные для моделирования работы отечественного здания.
Предварительно заметим, что максимальная длина очереди равна 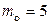 (так как только 5 мест для ожидания обслуживания на стоянке).
(так как только 5 мест для ожидания обслуживания на стоянке).
В системе имеется 3 бокса. Это и есть каналы обслуживания. Т.о. число каналов обслуживания равно 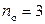 .
.
Интенсивность поступления отечественных автомобилей на станцию  . Это и есть интенсивность входящего потока.
. Это и есть интенсивность входящего потока.
Интенсивность обслуживания определяется через среднее время обслуживания как обратная величина:
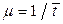 . (1)
. (1)
 .
.
Очевидно, измерять интенсивность обслуживания в автомобилях в минуту неудобно и ненаглядно. Переведем интенсивность из авт./мин в авт./день. С учетом того, что рабочий день на станции 12 часов, а в часу 60 минут, получим:
 .
.
II. Найдем входные данные для моделирования работы иностранного здания.
Предварительно заметим, что максимальная длина очереди равна  (так как только 3 места для ожидания обслуживания на стоянке).
(так как только 3 места для ожидания обслуживания на стоянке).
В системе имеется 2 бокса. Это и есть каналы обслуживания. Т.о. число каналов обслуживания равно 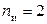 .
.
Интенсивность поступления иномарок на станцию 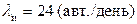 . Это и есть интенсивность входящего потока.
. Это и есть интенсивность входящего потока.
Интенсивность обслуживания определяется через среднее время обслуживания как обратная величина:
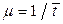 . (1)
. (1)
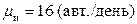 .
.
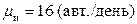 .
.
III. Определение параметров объединенной системы.
|
|
|
Параметры системы после объединения будем обозначать волной, например 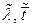 и т.п. Особое внимание при объединении следует уделить способам осреднения величин.
и т.п. Особое внимание при объединении следует уделить способам осреднения величин.
После объединения можно рассматривать систему как единую с общим числом бригад, общей стоянкой, обслуживающую все автомобили вместе. Тогда:
общее число бригад (каналов обслуживания) станет равно
 ;
;
общая длина очереди
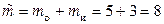 ;
;
общая интенсивность входящего потока
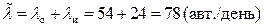 .
.
Сложнее определить среднюю интенсивность обслуживания одного «среднего» автомобиля «средней» бригадой. Она может быть вычислена по формуле:
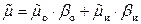 ,
, 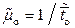 ,
,  ,
,
где 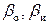 – доли «отечественных» и «импортных» бригад в объединенной станции;
– доли «отечественных» и «импортных» бригад в объединенной станции; 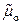 и
и 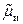 – средние интенсивности, а
– средние интенсивности, а 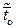 и
и 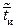 – средние времена обслуживания соответствующими бригадами одной машины объединенного потока. То есть интенсивность средней бригады получается как средневзвешенная по доле бригад интенсивность работы бригады каждого типа.
– средние времена обслуживания соответствующими бригадами одной машины объединенного потока. То есть интенсивность средней бригады получается как средневзвешенная по доле бригад интенсивность работы бригады каждого типа.
Средние времена обслуживания определяются как средневзвешенные по доле разного типа машин времена обслуживания бригадой машин каждого типа:
 ,
,
где 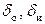 – доли «отечественных» и «импортных» машин в общем входящем потоке.
– доли «отечественных» и «импортных» машин в общем входящем потоке.

Заметим, что при осреднении бригад необходимо брать средневзвешенную по доле бригад интенсивность обслуживания, а для осреднения потока машин – средневзвешенное по доле автомобилей время обслуживания. Подставляя данные нашей задачи, получаем:
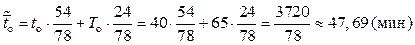 ,
,
 ,
,
 ,
,
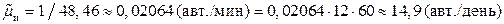 .
.
Тогда обобщенная интенсивность обслуживания равна:
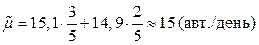 .
.
То есть интенсивность обслуживания упала из-за несоответствия квалификации.
|
|
|


